
|
定理・定義・公式集
このページはいざ問題を解くときに、忘れてしまった定理・定義・公式の
内容をすぐに思い出せるように様々な定理・定義・公式、
またその他問題を解くときによく使われる式などをまとめて紹介しています。
い え お か
き け さ
し す せ
そ た ち
て と な
に は ひ
ふ へ み
よ ら
移項
一方にある項を符号を変えてもう一方の項に移すこと。
<例>a+b=c→a+b-c=0
一般角の表わし方
θ+2nπ
θ+2n×360°
因数定理
xの整式P(x)においてP(α)=0がなりたつならP(x)は(x-a)で割り切れ、
逆にP(x)が(x-a)で割り切れるならP(α)=0。
<例>f(x)=x3-6x2+11x-6のとき、
f(1)=f(2)=f(3)=0より
f(x)は(x-1)、(x-2)、(x-3)で割り切れる。
因数分解
一つの多項式を複数の単項式、多項式の積に直すこと。
因数定理を使うとやりやすい。
<例>x2+3x+2=(x+1)(x+2)
<公式>
ma+mb=m(a+b)
ma-mb=m(a-b)
a2-b2=(a+b)(a-b)
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
x2+(a+b)x+ab=(x+a)(x+b)
円の性質
<弦>
一つの円または半径の等しい円において
弦の長さが長いほど弦と円の中心との距離は短くなる。
<接線>
円の接線は接点を通る半径に垂直である。その逆も成り立つ。
また一つの点からえんにひいた二つの接線には図のような性質ができる。
<面積・周>
半径rの円において
面積・・・・・・πr2
円周の長さ・・・・・・2πr
中心角a°に対する弧の長さ・・・・・・2πr×a/360
円の方程式
☆座標上を使っての方程式
円の中心をC(a,b)、半径をrとしたときに、
(x-a)2+(y-b)2=r2
と表わせる。
☆ベクトルを使っての方程式
中心の点をC、半径の長さをr、円周上の任意の点をPとしたときに、
A,Pの位置ベクトルをa,pとすると
|p-a|=r
または
(p-a)(p-a)=r2
と表わせる。
円周角の定理
円周角の定理とは
「同じ弧に対する円周角の大きさは等しく、
その弧に対する中心角の大きさの半分である。」
円順列
n個の異なるものを円の形にならべるとき、その場合の数は
nPn/n=(n-1)!
で計算できる。
扇形
半径r、中心角a°の扇形の面積・・・・・・πr2
半径r、弧の長さlの扇形の面積・・・・・・1/2rl
か行 トップ あ行 さ行 た行 な行 は行 ま行 や行 ら行
外心
三角形の三つの辺の垂直二等分線が交わる点。
三つの角から等距離にある点で、その点を中心に三角形の外接円がかける。
とくに直角三角形の外心は斜辺の中点である。
解と係数の関係
二次方程式ax2+bx+c=0の二つの解をα,βとするとき
α+β=-b/a
αβ=c/a
が成り立つ。
解の公式
二次方程式ax2+bx+c=0においてその解は
(-b±√[b2-4ac])/2a
と表わせる。
外分
a(A,B)、b(C,D)をm:nに外分する点cは
((mC-nA)/(m-n),(mD-nB)/(m-n))
で表わせる。
角の二等分線の性質
角の二等分線はその名の通り角を二等分するが、
と同時に角をなす2直線から等距離の点の集まりが
角の二等分線でもある。
確率
試行をたくさん繰り返したとき、その結果の相対度数がとある一定値に近づく。
この値を確率という。難しい説明だが、その値を求めるときは
その事象の起こる場合の数÷すべての場合の数
で求まる。
<例>一個のさいころを転がすとき1の目が出る確率は
その事象の起こる場合の数÷すべての場合の数
=1÷6=1/6
確率の加法定理
Aという事象とBという事象が同時に起きないときAまたはBが起きる確率は
P(A)+P(B)
で求めることができる。(P(x)はxという事象が起きる確率を示す。)
<例>
一個のさいころをふって3または1が出る確率は、1の目と3の目は同時に出ないので
1/6+1/6=1/3
確率の乗法定理
A,Bという二つの事象があり、一方の事象が起きる確率は
もう一方の事象の起きる確率が起きる確率とは無関係であるとき
(このときA,Bは独立しているという)、
A,Bともに起きる確率は
P(A)・P(B)
で表わせる。(P(x)はxという事象が起きる確率を示す。)
<例>さいころを二回ふったときに一回目に奇数、二回目に偶数が出る確率は、
3/6×3/6=1/4
加法の結合法則・交換法則
足し算をするときに次のような法則が成り立つ。
a+b=b+a
(a+b)+c=a+(b+c)
要するに足し算をするときは自由に順番を入れ替えて計算してよいということである。
完全平方式による方程式の解き方
一つの二次方程式が与えられたとき
(ax+b)2=c
の形に直し、
ax+b=√[c]
ax=√[c]-b
x=(√[c]-b)/a
とゆうように変形して解く方法。
しかし因数分解や、二次方程式の解の公式を使った方が速い。
軌跡
軌跡の問題の一般的な解き方。
①座標が与えられてないときは座標を適当に決める。
②求める軌跡上の点を(X,Y)などとおいて問題で与えられた条件をX,Yの方程式を立てる。
③②の結果から、図形を求める。
④できた図形のすべての点が問題の条件を満たすか確認する。
<例題>
点Aがx2+y2=16上を動くとき、
点Aと点B(9,0)を2:1に内分する点Pの描く軌跡を求めよ
P(X,Y),A(x,y)とおくと
X=(x+2×9)/3
Y=y/3
これをx,yについてとくと
x=3X-18
y=3Y
この二式をx2+y2=16に代入すると
(3X-18)2+9Y2=4
(X-6)2+Y2=(2/3)2
よってPは中心(6,0)半径2/3の円を描く。
期待値
多数の試行を行ったとき結果として出てくる数値の平均。
逆関数の求め方
①y=f(x)でxについて解く
②①の結果でxとyを入れかえる。
③はじめのy=f(x)の定義域を求めた逆関数の値域に、もとの値域を逆関数の定義域にする。
球
半径rの球があるとき
体積・・・・・・4/3πr3
表面積・・・・・・4πr2
共役複素数
複素数a+bi(a,bは実数)にたいしa-biを共役な複素数という。
複素数Aにたいし、共役な複素数を?と表わす。性質としては
A?=|A|2
があげられる。
近似値
<加法・減法の計算>
有効数字の末位が最も位の高いものにあわせて計算する。
<例>1.23+0.125
この場合1.23の末位は小数点第二位,0.125の末位は小数点第三位。
よって最も位の高い末位は小数点第二位なので0.125の小数点第三位を四捨五入して0.13
1.23+0.13=1.36
答え1.36
<乗法・除法の計算>
有効数字の最も桁数の少ないものに桁数をそろえて四捨五入して計算し、
その結果もその桁数にそろえて四捨五入する。
<例>1.2×123.45
このとき1.2の桁数2桁にそろえて123.45は120にする。
1.2×120=144
さらに144を2けたにして
答え1.4×102
☆最後に答えを
□.□□□・・・×10n
という形にするとよい。140は1.4×102
係数比較法
恒等式の両辺の同類項の係数を見比べて未知の係数を決定する方法。
<例>x2+2x+3=(a-1)x2-(b+1)x+2cのとき
1=a-1
2=-(b+1)
3=2c
より
a=2,b=-3,c=3/2
原始関数
→不定積分
さ行 トップ あ行 か行 た行 な行 は行 ま行 や行 ら行
錯角
右図において・・・・・(図が必要)
三角関数の加法定理
sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
三角関数の積を和に直す公式
sinαcosβ=1/2{sin(α+β)+sin(α-β)}・・・・・・①
cosαsinβ=1/2{sin(α+β)-sin(α-β)}・・・・・・②
cosαcosβ=1/2{cos(α+β)+cos(α-β)}
sinαsinβ=1/2{cos(α+β)-cos(α-β)}
ただしsin(α-β)=-sin(β-α)を考えると①と②は同じ事を言っている。
三角関数の和を積に直す公式
sinA+sinB=2sin((A+B)/2)cos((A-B)/2)
sinA-sinB=2cos((A+B)/2)sin((A-B)/2)
sinA+sinB=2cos((A+B)/2)cos((A-B)/2)
sinA+sinB=2sin((A+B)/2)sin((A-B)/2)
三角形の角の二等分線と対辺の交点
三角形の一つの角、およびその外角の二等分線は、
その対辺を他の二辺の比に内分、及び外分する。・・・・・・図を参照
三角形の合同条件
①三辺の長さが等しい
②2辺の長さとその挟む角の大きさが等しい
③一辺の長さとその両端の角の大きさが等しい
三角形の相似条件
①三辺の長さの比が等しい
②二辺の長さの比とその挟む角の大きさが等しい
③二角が等しい
三平方の定理とその逆
直角三角形△ABC(∠C=90°)において a2+b2=c2 が成り立つ。
逆に a2+b2=c2 であるなら、∠Cは直角である。
三角形の内角と外角
①三角形の内角の和は180°
②三角形の外角は、隣り合わない三角形の二つの内角の和に等しい
三角形の面積比
高さの等しい三角形の面積の比はその底辺の比に等しい。
四角形が円に内接する条件
向かい合う角の和が180°ならその四角形は円に内接する。
Σ
数列anにおいて第n項までの和Snは
Sn=a1+a2+a3+・・・・・+an
であるが、これを書き換えて
n
Σak
k=1
と表わす。
<代表例>
an=nのとき
n
Σn=1+2+3+・・・・・・n=1/2n(n+1)
k=1
an=n2
n
Σn2=12+22+32+・・・・・・+n2=1/6n(n+1)(2n+1)
k=1
an=n3
n
Σn3=13+23+33+・・・・・・+n3=1/4n2(n+1)2
k=1
指数法則
am×an=am+n
(am)n=amn
(ab)m=ambm
重心
△ABCにおいてABの中点をL、BCの中点をM、CAの中点をNとしたとき、
AM、BN、CLは一点で交わる。 この交点を重心という。
また重心は AM、BN、CLを2:1に内分する。
順列
いくつかのものを一列にならべることを順列という。
a個の中からb個とりだし順列を作る場合の数は aPbとかき、
a(a-1)(a-2)・・・・・・(a-b+1) と計算する。
(aからa-b+1までかけている数はb個ある) ようはaから1ずつ小さくしたものをb個
掛け合わせればよいのである。
乗法公式
m(a+b)=ma+mb
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(a+b)(a-b)=a2-b2
(x+a)(x+b)=x2+(a+b)x+ab
(ax+b)(cx+d)=acx2+(ad+bc)x+bd
(a+b)3=a3+3a2b+3ab2+b3
(a-b)3=a3-3a2b+3ab2-b3
(a+b)(a2-ab+b2)=a3+b3
(a-b)(a2+ab+b2)=a3-b3
乗法の結合法則、交換法則
a×b=b×a
(a×b)×c=a×(b×c)
ようはかけ算をするときはどんな順番でかけていってもよいということである。
剰余の定理
xの整式P(x)が(x-a)割られたときのあまりはP(a)で表わせる。
<例>P(x)=x4+x3+x2+xを(x-1)で割ったときのあまりは
P(1)=4
数値代入法
恒等式の両辺の変数に任意の数を代入して係数を求める方法。
x2+2x+3=(a-1)x2-(b+1)x+2cのとき
x=0のとき
3=2c・・・・・・①
x=1のとき
6=a-1-b-1+2c
a-b=5・・・・・・②
x=-1のとき
2=a-1+b+1+2c
a+b=-1・・・・・・③
①②③よりa=2,b=-3,c=3/2
正弦定理
△ABCにおいて a/sinA=b/sinB=c/sinC=2R(Rは△ABCの外接円の半径) が成り立つ。
正弦正接の加法定理
→三角関数の加法定理
整式の演算法則
A,B,Cを整式とした時に
AB=BA
A+B=B+A
(A+B)+C=A+(B+C)
(AB)C=A(BC)
A(B+C)=AB+AC
が成り立つ。
ようは数字での交換、結合、分配法則が整式でも成り立つということである。
積分
不定積分、定積分、置換積分、部分積分の項を参照。
接弦定理
円において弦の一端における接線が弦となる角は、
その角をなす二直線の中の円の弧に対する円周角と等しい。
言葉ではわかりにくいと思うので、図を載せておく。・・・・図が必要
接線の方程式
y=f(x)上の点(a,f(a))における接線の式は
y=f'(x)(x-a)+f(x)
素因数分解
素因数分解とはとある数を素数の積の形で表わすこと。
右の図のよう小さい順に素数を考え、その数が素数で割れるかどうか考えながらやるとよい。
<例>360=23×32×5
相加相乗平均の関係
0より大きい数a,bにおいて
(a+b)/2≧√[ab]
が成り立つ。イコールとなるのはa=bの時である。
相似な図形の比
<平面図形>
周の長さの比・・・・・・相似比に等しい
面積比・・・・・・相似比の二乗に等しい。
<立体図形>
対応する曲線や線分の比・・・・・・相似比に等しい
対応する面の面積比・・・・・・相似比の二乗に等しい。
体積の比・・・・・・相似比の三乗に等しい。
た行 トップ あ行 か行 さ行 な行 は行 ま行 や行 ら行
対称な関数
y=f(x)のとき
原点対称の関数・・・・・・y=-f(-x)
x軸対称の関数・・・・・・y=-f(x)
y軸対称の関数・・・・・・y=f(-x)
対称な点の座標
P(a,b)のとき
原点対称の点・・・・・・(-a,-b)
x軸対称の点・・・・・・(a,-b)
y軸対称の点・・・・・・(-a,b)
体積
r=半径
円柱・角柱・・・・・・(底面積)×(高さ)
円すい・角すい・・・・・・(底面積)×(高さ)×1/3
球・・・・・・4/3πr3
対頂角
対頂角は等しい。
代入法
連立方程式において、一つの文字についてとき、
その結果をもう一方の式に代入して解く方法
<例>3x-y=-3・・・・・・①
x+2y=-1・・・・・・②
の時、①をyについてとくと
y=3x+3
これを②に代入すると
x+2(3x+3)=7x+6=-1
7x=-7
x=-1
y=0
多角形の内角と外角
①n角形の内角の和は2(n-2)×90°
②n角形の外角の和は常に360°
置換積分
複雑な積分を解くとき置換積分法を使うときがある。
∫f(x)dx=∫f(g(t))g'(t)dt ただしx=g(t)
∫f(g(x))g'(x)dx=∫f(t)dt ただしt=g(t)
<例>∫sin2xcosxdxのときt=sinxとおくと
dt/dx=cosxより
(与式)=∫t2dt
=∫tdt
=1/2t2
=1/2sin2x
中点連結定理とその逆
辺AB、ACの中点をM,Nとすれば、
BC//MN,MN=1/2BC
が成り立つ。
△ABCにおいて、辺AB,ACの
逆に△ABCにおいて、辺ABの中点Mを通り、
BCに平行な直線とACとの交点をNとすると、
AN=1/2AC,MN=1/2BC
が成り立つ。
直線の式の求め方
①傾きがa、切片がbの直線の式はy=ac+b
②傾きがでa点(m,n)を通る直線の式はy-n=a(x-m)
③2点(a,b)(m,n)を通る直線の式は
y-n={(b-n)/(a-m)}(x-m)
直角三角形の合同条件
①斜辺と一鋭角が等しい
②斜辺ともう一辺が等しい
定積分
F(x)がf(x)の不定積分のとき
F(b)-F(a)
をf(x)のaからbまでの定積分という。
∫abf(x)dx=F(b)-F(a)
と表わす。この右辺は[F(x)]abとかかれる。
同位角
右図のように・・・・・・図が必要
等式の性質
a=bのとき
①a+c=b+c
②a-c=b-c
③ac=bc
④a/c=b/c
等積変形
元の図形から同じ面積の形の違う図形を作ること。
平行線を使うとうまく行く場合が多い・・・・・・図が必要
同側内角
右図のように平行線における180°
(なぜなら平行線において同位角、錯角は等しいから)
→詳細:円の性質
な行 トップ あ行 か行 さ行 た行 は行 ま行 や行 ら行
内心
三角形の内接円の中心を内心という。
内心は三角形の3つの角の二等分線の交点である。(3つの線は一点で交わる。
また、内心は三角形の3辺から等距離にある。)
内分点
二つの点a(A,B),b(C,D)が与えられたときabをm:nに内分する点は
((mC+nA)/(m+n),(mD+nB)/(m+n))
で表わされる。
二項定理
(a+b)n
=nCnan+nCn-1an-1b+nCn-2an-2b2+ ・・・・・・+nCn-kan-kbk+・・・・・・+nC1abn-1+nC0bn
二倍角の公式
加法定理から次の公式が得られる。
sin2α=2sinαcosα
cos2α=cos2α-sin2α
=2cos2α-1=1-2sin2α
tan2α=2tanα/(1-tan2α)
は行 トップ あ行 か行 さ行 た行 な行 ま行 や行 ら行
場合の数
とある試行を行ったとき起こりうる全ての数を場合の数という。
順列、組合せなどがよく問題としてだされる。
媒介変数
xとyの関係をx,yで直接式にして表わさず、
また別の変数(媒介変数、tなど)を用いてx,yの関係を表わす方法。
媒介変数を使っての問題はまず一方の式でその媒介変数についてといて、
もう一方の式に代入することでたいがい解ける。
<例>次のようにx,yが表わされるとき、x,yの関係を求めよ。
x=3+2t・・・・・・①
y=6t-3・・・・・・②
のとき①を変形して、
t=(x-3)/2
これを②に代入すると、
y=3(x-3)-3
=3x-12
半角の公式
sin2(α/2)=(1-cosα)/2
cos2(α/2)=(1+cosα)/2
tan2(α/2)=(1-cosα)/(1+cosα)
判別式
二次方程式ax2+bx+c=0が与えられたとき
b2-4ac>0のとき実数解が二つ
b2-4ac=0のとき重複解
b2-4ac<0のとき虚数解が二つ(虚数の範囲を除くときは解なし)
また、y=ax2+bx+cが与えられたときx軸との交点の数は
b2-4ac>0のとき二個
b2-4ac>0のとき一個
b2-4ac>0のときなし
ピタゴラスの定理
→三平方の定理
微分
ここに基本的な微分の公式をあげておく。
(xa)'=axa-1
(sinx)'=cosx
(cosx)'=-sinx
(tanx)'=1/cos2x
(ex)'=ex
(logx)'=1/x
表面積
角柱(底面積s)・・・・・・(底面積)×2+(側面積)
角すい(底面積s)・・・・・・(底面積)+(側面積)
円柱(底面の半径r、高さh)・・・・・・2πr2+2πrh
円すい(底面の半径r、母線の長さl、高さh)・・・・・・πr2+πrl
球(半径r)4πr2
比例・反比例
y=ax(aは0以外の定数)のときyはxに比例するといい、aを比例定数という。
xy=a(aは0以外の定数)のときyはxに反比例するといい、aを比例定数という。
不定積分
ここに基本的な積分の公式を書いておく
xa→xa+1/(a+1) + C
cosx→sinx+C
sinx→-cosx+C
1/x→logx+C
ex→ex+C
すべて微分と反対の作業を行っているわけで微分に十分なれておくことが大切。
不等式の性質
a>bのとき
①a+c>b+c,a-c>b-c
②c>0のとき ac>bc, a/c>b/c
③c<0のとき bc>ac, b/c>a/c
部分積分
∫f(x)g(x)dx=F(x)g(x)-∫F(x)g'(x)(F(z)はf(x)の原始関数)
分配法則
a(b+c)=ab+ac
分母の有理化
分母にある根号をふくむ数を変形して分母に根号を含まないようにすること。
<例1>
3/2√[2]
=(3×√[2])/(2√[2]×√[2])
=3√[2]/4
<例2>
√[2]/(√[5]-√[3])
=√[2](√[5]+√[3])/(√[5]-√[3])(√[5]+√[3])
=√[10]+√[6]/2
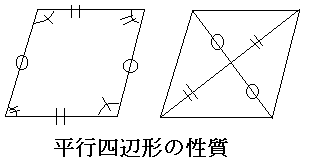
平行四辺形
<性質>
(1)向かい合う辺の長さが等しい
(2)向かい合う角の大きさが等しい
(3)二本の対角線は互いにもう一方を二等分する。
<平行四辺形である条件>
(1)二組の向かい合う辺が平行
(2)二組の向かい合う辺の長さが等しい
(3)一組の向かい合う辺の長さが等しく、平行
(4)二組の向かい合う角の大きさが等しい
(5)対角線が互いにもう一方を二等分している
平方完成
二次方程式ax2+bx+cが与えられたとき次のように変形する。
ax2+bx+c
=a(x2+b/ax)+c
=a{x2+b/ax+(b/2a)2}+c-(b/2a)2
=a(x+b/2a)2+c-b2/4a2
この方法で二次関数y=ax2+bx+cのグラフを書くときにその頂点の座標 (-b/2a,c-b2/4a2)が分かる。
平方根
<大小>
a>b>0のときa>bならば√[a]>√[b]、√[a]>√[b]ならばa>b
<加法・減法>
m√[a]+m√[b]=m(√[a]+√[b]),m√[a]-m√[b]=m(√[a]-√[b])
<乗法・除法>
√[a]√[b]=√[ab],a√[b]=√[a2]b,√[a]/√[b]=√[a/b],√[b]/a=√[b/a2]
変位
変化の割合
(変化の割合)=(yの増加量)/(xの増加量)
変曲点
グラフ上で上に凸な部分と下に凸な部分との変わり目を変曲点という。
y=f(x)が与えられたときf(x)を二度微分したf''(x)が0となるxが変曲点のx座標である。
ま行 トップ あ行 か行 さ行 た行 な行 は行 や行 ら行
未定係数法
恒等式の性質を用いて恒等式の未知の係数を求める方法。係数比較法と数値代入法がある。
や行 トップ あ行 か行 さ行 た行 な行 は行 ま行 ら行
余弦定理
△ABCにおいて
a2=b2+c2-2bccosA
b2=a2+c2-2accosA
c2=a2+b2-2abcosA
が成り立つ。
余弦の加法定理
→三角関数の加法定理
ら行 トップ あ行 か行 さ行 た行 な行 は行 ま行 や行
ラジアン
単位円の中心角をθとしたとき、その中心角θをもつ扇形の弧の長さでθを表わす方法をラジアンという。
<例>1/6π=30°
π=180°
5/3π=300°