一次関数
<一次関数とは>
一つの変数の一次式で表わされる関数のこと。この変数というのにはおもにxが使われる。
(例)y=3x+2のときyはxの一次関数である。
*ちなみに比例というのは一次関数である。
<一次関数のグラフ>
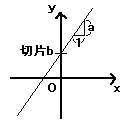  y=ax+bという関数をグラフに表わすと傾き y=ax+bという関数をグラフに表わすと傾き
(xが1増加したときyがいくら増加するか)a、
y切片(グラフのy軸との交点のy座標)bの直線である。
(左図)
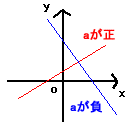
◎傾きaが正のとき、グラフは右上がり、
負のときは右下がりとなる。(右図)
◎y=ax+bのグラフとy=cx+dのグラフにおいて
①a=c,b≠dのとき二つのグラフは平行
②a=c,b=dのとき二つのグラフは一致(重なる)
③a≠c,b≠dのとき二つのグラフは一点で交わる。
◎グラフをかくときはとにかく一次関数の式を満たす(x,y)の組を適当に見つけ、
その二点を座標上にかき、その二点を結ぶ直線を引く。
(例)y=3x+2においてx=0のときy=2だから、このグラフは(0,2)を通る。またx=1のときy=5だから、
このグラフは(1,5)を通る。よって点(0,2)、点(1,5)を座標上にかきこの二点を結べばよい。
☆直線のグラフの式を求める(公式)
①傾きがa、切片がbの直線の式はy=ac+b
②傾きがでa点(m,n)を通る直線の式はy-n=a(x-m)
③2点(a,b)(m,n)を通る直線の式は
y-n={(b-n)/(a-m)}(x-m)
方程式と一次関数のグラフの関係
①連立方程式とグラフの関係
 連立方程式
ax+b=c
dx+e=f
においてその解(m,n)と、一次関数ax+b=c,dx+e=fの
それぞれのグラフの直線の交点の座標(m',n')において
(m,n)と(m',n')は一致する。
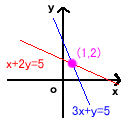
ちょっと難しそうに聞こえるが、例を挙げよう。連立方程式
x+2y=5, 3x+y=5
の解を求めると、(1,2)になる。
またx+2y=5,3x+y=5のグラフを書いて交点を見ると(1,2)になっている。
さらにこのことから、連立方程式が与えられたとき、二つの式をグラフ上に表わし、
二つの直線が交わるなら解が一つ、平行なら交点がないので解なし、一致しているのなら
(交点が無限にあるのと同じなので)解は無数にある。 連立方程式
ax+b=c
dx+e=f
においてその解(m,n)と、一次関数ax+b=c,dx+e=fの
それぞれのグラフの直線の交点の座標(m',n')において
(m,n)と(m',n')は一致する。
ちょっと難しそうに聞こえるが、例を挙げよう。連立方程式
x+2y=5, 3x+y=5
の解を求めると、(1,2)になる。
またx+2y=5,3x+y=5のグラフを書いて交点を見ると(1,2)になっている。
さらにこのことから、連立方程式が与えられたとき、二つの式をグラフ上に表わし、
二つの直線が交わるなら解が一つ、平行なら交点がないので解なし、一致しているのなら
(交点が無限にあるのと同じなので)解は無数にある。
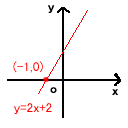 ②一次方程式ax+b=0の解はy=ax+bのグラフのx軸との交点にあたる。
またまた難しそうに聞こえるが、ax+b=0を解くことは
ax+b=y , y=0
という連立方程式においてxを解くに等しいから、
(なぜなら、下の式のyを上の式に代入すれば与えられた一次方程式になる。)
先ほどと同じに考えると、
y=0の直線(x軸)とy=ax+bとの交点のx座標を求めるに等しい。
(例)2x+2=0の解は-1、
またy=2x+2の交点を求めると(-1,0)となり、
やはりx座標は-1である。 ②一次方程式ax+b=0の解はy=ax+bのグラフのx軸との交点にあたる。
またまた難しそうに聞こえるが、ax+b=0を解くことは
ax+b=y , y=0
という連立方程式においてxを解くに等しいから、
(なぜなら、下の式のyを上の式に代入すれば与えられた一次方程式になる。)
先ほどと同じに考えると、
y=0の直線(x軸)とy=ax+bとの交点のx座標を求めるに等しい。
(例)2x+2=0の解は-1、
またy=2x+2の交点を求めると(-1,0)となり、
やはりx座標は-1である。
 ③一次方程式ax+b=cx+dの解は
y=ax+b,y=cx+dのグラフの交点のx座標である。
これも②と同じようにax+b=cx+dを解く事は連立方程式
y=ax+b, y=cx+d
を解く事に等しいから
(なぜなら、下の式のyを上の式に代入すれば、与えられた方程式になるから)
あとは①の考え方にあてはめる。
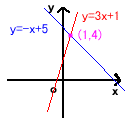
例3x+1=-x+5において解は1になるが、
y=3x+1,y=-x+5のグラフをかくと、
交点は(1,4)となりやはりx座標は1となる。 ③一次方程式ax+b=cx+dの解は
y=ax+b,y=cx+dのグラフの交点のx座標である。
これも②と同じようにax+b=cx+dを解く事は連立方程式
y=ax+b, y=cx+d
を解く事に等しいから
(なぜなら、下の式のyを上の式に代入すれば、与えられた方程式になるから)
あとは①の考え方にあてはめる。
例3x+1=-x+5において解は1になるが、
y=3x+1,y=-x+5のグラフをかくと、
交点は(1,4)となりやはりx座標は1となる。
|

y=ax+bという関数をグラフに表わすと傾き
連立方程式 ax+b=c dx+e=f においてその解(m,n)と、一次関数ax+b=c,dx+e=fの それぞれのグラフの直線の交点の座標(m',n')において (m,n)と(m',n')は一致する。 ちょっと難しそうに聞こえるが、例を挙げよう。連立方程式 x+2y=5, 3x+y=5 の解を求めると、(1,2)になる。 またx+2y=5,3x+y=5のグラフを書いて交点を見ると(1,2)になっている。 さらにこのことから、連立方程式が与えられたとき、二つの式をグラフ上に表わし、 二つの直線が交わるなら解が一つ、平行なら交点がないので解なし、一致しているのなら (交点が無限にあるのと同じなので)解は無数にある。
②一次方程式ax+b=0の解はy=ax+bのグラフのx軸との交点にあたる。 またまた難しそうに聞こえるが、ax+b=0を解くことは ax+b=y , y=0 という連立方程式においてxを解くに等しいから、 (なぜなら、下の式のyを上の式に代入すれば与えられた一次方程式になる。) 先ほどと同じに考えると、 y=0の直線(x軸)とy=ax+bとの交点のx座標を求めるに等しい。 (例)2x+2=0の解は-1、 またy=2x+2の交点を求めると(-1,0)となり、 やはりx座標は-1である。
③一次方程式ax+b=cx+dの解は y=ax+b,y=cx+dのグラフの交点のx座標である。 これも②と同じようにax+b=cx+dを解く事は連立方程式 y=ax+b, y=cx+d を解く事に等しいから (なぜなら、下の式のyを上の式に代入すれば、与えられた方程式になるから) あとは①の考え方にあてはめる。 例3x+1=-x+5において解は1になるが、 y=3x+1,y=-x+5のグラフをかくと、 交点は(1,4)となりやはりx座標は1となる。