二乗に比例する関数

さて、いよいよ中学数学の代数系最後の項目二乗に比例する関数。
前にやった比例の関数とは y=ax という形で表わされた。
これは言い換えれば変数xの一乗に比例する関数といえる。
今回扱う二乗に比例する関数とは y=ax² という形で表わされるものである。
yはxの二乗に比例するといい、aは普通の比例の関係式同様比例定数と呼ばれる。
さてこの時点での問題としては次のようなのが出てくる。
(例)yはxの二乗に比例し、xが2のとき、yは12である。
比例定数はいくつか。
〔解法〕比例定数をaとおくと、 2²×a=12 a=3
まぁ、ものすごく基本的な問題ではあるが。

さて関数にはつきもののグラフ。これをえがくと上のようになる。なぜ二通りかいてあるかというと比例定数の値によってグラフの向きが変わってくるからである。比例定数が正の時グラフは上開き(下に凸)に、比例定数が負の時グラフは下開き(上に凸)となる。また普通の比例と同じように比例定数の絶対値が大きくなるほどグラフは細く傾き具合が急になっていく。この事を知っていれば例えばたくさんの二乗に比例する関数のグラフが同一座標上にえがかれているときなど、比例定数の値によってどれがどの関数かわかる。

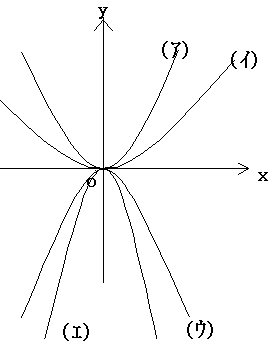(例)次の関数は上のグラフの(ｱ)〜(ｴ)のどれか。
(1)y=x²
(2)y=-2x²
(3)y=-3x²
(4)y=x²/2
まずグラフがx軸より上かどうかで二つに分け、
さらにグラフの傾き具合でえらぶと答えは
(1)(ｱ)(2)(ｳ)(3)(ｴ)(4)(ｲ)

二乗に比例する関数の性質に関する問題が
出るときがあるが、 先にあげたグラフの形を
思い描いて考えればたいがい解ける はずである。
(例)x>0の範囲においてxが増加すると、
yが減少するのは次の関数のうちどれか。
�@y=x²
�Ay=3x²
�By=-2x²
この場合グラフをかいたとき
上開きか下開きかを考える。
グラフが下開きならx>0の範囲で、
yはどんどん値が下がっていく。
よってグラフが下開きのものを考えると
�Bしかない。答えは�B。

さてここで、一次関数では
出てこなかった言葉が出てくる。
それが｢変化の割合｣というものである。
これはyの増加量をxの増加量で割ったものである。
二乗に比例する関数のグラフにおいて二点M(a,c),N(b,d)があり、
xの値がaからbまで増加するときの変化の割合を式で表わすと
(yの増加量)/(xの増加量)=d-c/b-a

注意すべきこととして
�@上の場合引き算の順序が(Nの数)-(Mの数)の順序であるが、
これは逆でもよい。ただし、分母と分子の引き算の順序が別々になってはいけない。
d-c/a-bというのはだめ。
�A｢増加量｣という言葉が気にかかると思うが、分母･分子それぞれの計算結果が
マイナスになっても気にしなくてよい。 さてこれはちょっとした公式まがいなのだが、
実際にy=ax²においてxがmからnに変化するときの変化の割合を計算してみると
an²-am²/n-m =a(n²-m²)/n-m
乗法公式a²-b²=(a+d)(a-d)をつかって
=a(n+m)(n-m)/n-m =a(n+m)
(これはn-mが0でないとき、つまりnとmが等しくないときn-mで分母分子を割る)
通常変化の割合を聞いてくるときxの二つの値が同じという問題はまずない。
よってだいたいの変化の割合を求める問題においては y=ax²において
xがmからnに変化するときの変化の割合は a(n+m) という関係を用いることができる。

一次関数では変化の割合という言葉が出なかったと言ったが、
実際同じ要領 (yの増加量)/(xの増加量) でy=ax+bの増加量を計算してみると、
いつでもxの係数aに等しくなる。
だからあえて変化の割合という言葉を使う必要がなかったのである。
これで二乗に比例する関数の基本事項は終わり。あとは応用問題があるのだがそれは
図形、正三角形･平行四辺形などの図形と組合せて出てくる問題が結構ある。
大切なのはそれらの図形の基本的な性質と
その性質が座標の上ではどのように表われてくるのか、 の二つであろう。
ここではあえて取り上げない。というのも考え出したらきりがないほど多彩に問題ができてしまい、
それらの一つ一つを取り上げていては非常に多くの時間を取られてしまう。
市販の問題集にはいろいろこの手の問題がのっていると思うからそれをやるとよい。
すべての問題が解けなくても解こうとすることで問題の解き方になれることができればよい。