三角形の五心(うち重心、内心、外心)
とある三角形があるときその三角形における特殊な点というのが存在する。
それらのうちこのページでは重心、内心、外心についてみていく。
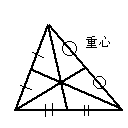 まず重心から。 まず重心から。
三角形のとある頂点から対辺(その角が触れてない辺。
例えば△ABCで∠Aの対辺はBC)の中点に引いた線を中線と呼ぶが、
三角形においては中線は三つ存在する。この三つの中線は一点で交わり、
しかもこの交点はそれぞれの中線を図のように1:2に内分する。
この交点のことを重心とよぶ。ちなみに重心という言葉は数学に限らず聞く
言葉だと思うが、三角形の板があったときこの重心の部分だけを支えれば
この三角形の板は落ちることがないというありがたい点である。
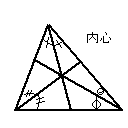 次に内心。 次に内心。
三角形には三角形の内部にあり、三角形の三辺に接する円が存在する。
そしてこの内接円の中心が内心とよばれる。
実際三角形のなかに内接円がある図を見ると分かると思うが、
この内心という点、三角形の三辺から等距離にある点である。
(円の半径は常に一定だから)辺と辺から等距離にある点と聞いたら
何かを思い出さないだろうか。平面図形の説明のページにもあったが、
角の二等分線とはその角をなす二直線から等距離な点の集まりであった。
よって内心から三つの角に直線を引くとそれは皆角の二等分線になる。
逆に言うと三つの角の二等分線は一点で交わり、それが内心となる。
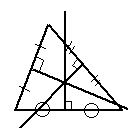 最後に外心。 最後に外心。
三角形は必ず外接円というものも作れる。
外接円とはその円周が三角形の三つの頂点を全て通る円のことである。
そしてこの外接円の中心が外心と呼ばれる。円周というのは中心の点から
等距離な点の集まりだから、逆に見れば外心は三角形の三つの頂点から
等距離な点でもある。さてこれでまた思い起こさないだろうか。
内心では角の二等分線が出てきたが、外心は線分の垂直二等分線が関わってくる。
そもそも線分の垂直二等分線はその線分の両端の点から等距離な点の集まり
であった。よって外心から三角形の三辺に垂線を下すと、その垂線の足は
それぞれ三辺を二分する。逆に言うと三つの辺の垂直二等分線は一点で交わり、
それが外心となる。
一応今まで説明した五心のうち三つについて位置について注意しておく。
重心というのは中線上にあるので三角形の内部にあり、
内心は三角形の内部にある内接円さらに内側にあるので当然三角形の内部にある。
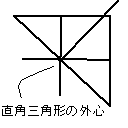
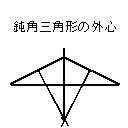
が、外心においては三角形の種類によって違ってくる。
三角形が鋭角三角形だったら外心はその内部に、
三角形が鈍角三角形だったら外心は三角形の外側に、
そして三角形が直角三角形だったら外心はその斜辺の中点にくる。
|

まず重心から。
次に内心。
最後に外心。

