平行線の比

実際平行線の比というものを見る前に内分点と外分点について知っておこう。
とある線分ABがあり、その内部に点PがありAP：PB=m：nのとき、
点PはABをm：nに内分しているという。

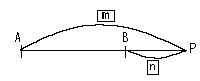
逆に外分というのは線分ABの延長線上に点Pがあり線分ABの内部にはないとき、
APの長さとPBの長さを比でm：nというように表わす。

このとき、mがnより大きいかどうかで
点Pの位置が変わってくるときに注意。
例えばAP：PB=3：1というときは上の線分のように位置するが、
AP：PB=1：3だと左の線分のように点Pは位置する。
次に平行線における比というものを見ていこう。

左のように図があった場合
次のような関係が成り立つ。
�@AB:AD=AC:AE=BC:DE
�AAD:DB=AE:EC
�BAB:DB=AC:EC
また、三角形に限らず上のような平行線に
区切られている場合でも同じような関係が成り立つ。

ここに平行な直線l,m,nがあるとする。
さらにこの3直線に交わる二本の直線をそれぞれa,bとする。
ここでできる六つの交点を図のようにAからFまで名をつける。
ここで AB:BC=DE:EF が成り立つのが分かるだろうか。
見た感じではそんな気もすると思うが一応説明しておく。
まず線分AFを引く。そしてAFとBEの交点をMとする。
△ABMと△ACFは相似なのでこれは平行線の関係ですぐ分かるはず）
AB:AC=AM:AF よってAB:BC=AM:MF･･････�@
おなじく△FMEと△FADは相似なので、
FM:FA=FE:FD よってFM:MA=FE:ED･･････�A
�@�AよりAB:AC=AM:AFがなりたつ。
この関係はよく使われるので覚えとくこと。
（最も見てすぐに気付きやすいと思うが） また、この平行線の比から導くことができる定理に
中線連結定理というものがある。
文章で表わすと｢三角形の二辺の
中点を結ぶ線は残りのいっぺんに平行で、
長さはその辺の半分である｣というものである。
左の図で言うと、三角形ABCにおいて
DE//BC
DE=(1/2)BC
という関係が成り立つ。 また台形においても
｢平行でない二辺の中点を結ぶ線は残りの二辺に平行で長さは残りの二辺を足して二で割ったものになる。｣
という関係が成り立つ。
上の図で言うと台形ABCDにおいて
AD//EF//BC
EF=(1/2)(AD+BC) が成り立つ。

さてここでついでに三角形の面積の比についてちょっと触れておこう。
左のような図があったとき、△ABDと△ADCの面積の比はどうなるか
ということである。二つの三角形の高さを考えると二つの
三角形をあわした△ABCと同じたかさである。
よって二つの三角形のBD=m、DC=nとおき、
二つの三角形の共通の高さをhとおくと、
三角形の面積の比は m×h×1/2：n×h×1/2=m：n となり、
底辺の長さの比になる。理屈はとにかく上のように二つの
三角形がくっついたような時は、その面積比は底辺の比になるということだけを覚えて使えるようにしておこう。
(例)△ABCにおいてABの中点をM、ACを2：1に内分する点をNとおくと、
△AMNの面積は△ABCの面積の何倍になるか。
〔解法〕補助線MCを書き込むと
(△AMCの面積)：(△ABCの面積)=AM：AB=1：2
よって△AMCの面積は△ABCの面積の1/2倍。
そして (△AMNの面積)：(△AMCの面積)=AN：AC=2：3
よって△AMNの面積は△AMCの面積の2/3倍。
よって △AMN=△AMC×(2/3) =(△ABC×(1/2))×(2/3)
=△ABC×(1/2)×(2/3) =△ABC×(1/3) よって△AMNは△ABCの1/3倍。
これは今非常に丁寧に解いているがなれてしまえば即座に (1/2)×(2/3)=1/3
と頭の中で計算できるようになってしまう。というか、三角形の面積比のさらに応用の問題では
いちいちこんなていねいな説明はかかず、即座に1/3倍と頭の中で出た結果をそのまま使ってしまうのが
普通である。逆に言うと頭の中で即座にできるくらいなれてしまわないと応用問題を解くときに
非常に苦労してしまう。はやくこの計算の仕方になれてしまおう。