平面図形
平面図形をやるにあたって、次に挙げる言葉は覚えておこう。
おそらく知っている言葉も多く、確認に近くなるからおそらく楽なはずだ。
<語句>
直線･･････無限の長さを持つまっすぐな線。直線ABというと二点ABを通るまっすぐな線。
半直線･･････一つの点から無限に伸びるまっすぐな線。
半直線ABというとAから始まり、Bを通るまっすぐな線。
線分･･････二点間を結ぶまっすぐな線。線分ABというと点Aと点Bを結ぶまっすぐな線。
角･･････一つの点を二つのまっすぐな線が通るとき、その二つの線がなす図形。
また、角をなしている二つの線を辺、辺が交わる所を頂点という。
円･･････一つの点から等距離にある点の集まり。
弧と中心角･･････弧は円周の一部で、元の円の中心Oと弧の両端の点A、Bを結んでできる
∠AOBがその弧に対する中心角という。
鋭角・鈍角・直角･･････0°から180°までの角のうち90°より小さいのを鋭角、
大きいのを鈍角という。
垂直･垂線･･････２直線l,mが作る角が直角のとき二直線l,mは垂直であるといい、l⊥mと表わす｡
垂線はとある直線にたいして垂直な直線のこと。
元の直線と垂線との交点を垂線の足というときもある。
 平行･･････２直線l,mがどこまでいっても交わらないとき、
l,mは平行であるといい、 l//mと表わす｡
別の言い方をするととある直線lが与えられたとき、
直線lと距離が等しい点の集まりともいえる。
点と点の距離･･････二つの点を結ぶ線分の長さ
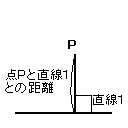
点と直線の距離(左図)･･････点Pから直線lに垂線を引くとき
(点Pを通る直線lに垂直な線分を引くときこの様に表現する)、
垂線と直線lとの交点をQとすると、PQが点Pと直線lの距離になる。
<コンパスと定規を使った作図>
コンパスと定規(この時定規は直線を引くためのもので長さは測れないとする)
をつかっての作図は次の六つがある。
文字で見ても分からないと思うから下の動画を見て理解して欲しい。
実際に紙とコンパス･定規を使ってやるのはさらによい。
①線分の垂直二等分線を引く｡
コンパスで線分の両端を中心とし、半径を同じくする円をかき、円の二つの交点を結ぶ。
ただしその半径は線分の長さの半分よりおおきくなくてはならない。
ちなみに、この線分の垂直二等分線とはその線分の両端の点から等距離にある点
の集まりともいえる。これが結構重要。
②直線上の点からその直線に垂直な直線をかく。
その点を中心とする円をかきその円と直線と交わる2点をP,Qとするとき、
P,Qを中心とし半径の長さが同じな円を二つかき、円と円との二つの交点を結ぶ。
③直線上にない点からその直線に垂直な直線をかく。
その点を中心とする円をかきその円と直線との交点をP,Qとするとき、
P,Qを中心とし半径の長さが同じ円を二つかき､円と円との交点と最初に与えられた点を結ぶ。
④角の二等分線をかく。
頂点を中心とした円をかき、その円と角をなす二つの線との交点をP､Qとするとき、
P､Qを中心とし半径の長さの等しい円を二つかき円と円の交点と角の頂点を結ぶ。ちなみに、
この角の二等分線はその角をなす二つの直線から等距離にある点の集まりともいえる。これが結構重要。
⑤直線上にない点からその直線に平行な直線をかく。
与えられた点をP、直線をlとするときまず点Pを中心とする円をかき、
その円と直線lとの交点をA,Bとおく。
次に点Bを中心とし、半径の長さがPBの長さである円をかく。
そして、点Pを中心とし、半径の長さがABと等しい円をかく。
最後にかいた二つの円の交点と点Pを結ぶ。
⑥角を移す。
∠ABCが与えられたとき、まず適当な長さで点Bを中心に円をかき、
円と半直線BA、BCとの交点をそれぞれD、Eとおく。次に別の場所に適当な半直線OXをかき、
点Oを中心に先ほどと同じ大きさの円をかき、半直線OXとの交点をMとおく。
そして、コンパスで線分DEの長さを取り、点Mを中心とした円を長さをとったコンパスでかく。
点M中心の円と点O中心の円との交点をNとすると、∠MONが∠ABCと等しくなっている。
これらの説明のなかには円をかくという作業が多く含まれているが
一番欲しいのはその円と何かの交点であり、
円周のうち交点付近以外の部分は必要ないといえる。
よって実際作図するときは｢交点はここらへんだ｣と思った付近だけの弧をかけばよい。
では次に図形の移動を考えてみよう。
平面図形において考えられる移動の種類として主に次の三つがある。
①平行移動
これは一つの図形が与えられたとき向きを変えないでそのままずらしていくこと。
②回転移動
与えられた図形のおのおのの点を、とある点を中心に回転させること。
特に180°回転させるときは点対称移動ともいい、
元の図形の任意の点と中心の点との距離は、
その任意の点に対応する移動しできた図形の点と中心の点との距離と等しい。
もうこれは文を読んで理解するよりは上の図を見て理解してくれ。
これを書いている自分自身もこんがらがってわけが分かんなくなってきた。
③線対称移動
とある直線を軸と定め、元の図形の任意の点とその点に対応する移動後の図形の点
それぞれの軸との距離が等しいようにしてできる。
この移動をテーブルの上に三角形の紙などを置いてやってみると
紙を裏返しにするという作業が入ってくることに気付くだろう。
さてこれらの三つの移動をすると二つの合同な図形をいつかは一つに重ねることができる。
合同というのは大きさ形全てが同じということである。
その合同な二つの図形が片方が裏返しになっていたら線対称移動をし、
向きが違うなら回転移動で向きをそろえ、最後に平行移動すれば重なるはずである。
|
