 |
 |
 |
 |
 |
|
空間図形
まず空間図形の基本、平面から見ていこう。
といっても平面図形を扱うわけではなく、いったいどうやったら、
具体的に言うといくつの点を定めれば平面が決定するのかということを考えるのである。
仮に一つの点が与えられてもその点をふくむ平面は無限にある。
もし、二つの点が与えられれば、
その二点をふくむ一つの平面をその二点を結ぶ直線を軸に回転させると
やはりたくさん平面ができてしまう。
では点が三つならどうか。頭で思い描いてみよう。
3点を通る平面が何個もあるだろうか。いや、ない。
点が三つあれば平面が一つに定まることが分かった。
また直線というのは二つの点が決まれば一つに決まる。
2+1=3で一つの直線と一つの点が定まればこれもまた平面は一つに決まる。
その他平行な二直線、交わる二直線でも平面がひとつに決まる。
では空間内における図形と図形の位置関係を見ていこう。
まずは直線と直線の関係。平面図形においては直線と直線といえば、
平行か交わるかのどちらかだったが、空間内においてはもう一つねじれの位置というものが出てくる。
ねじれの位置って何だと思うかもしれないが、これは二直線が同一平面上にないということを示している。
(平面図形ではとある一つの平面上での話だったのでねじれの位置が出てこないのは当然でもある)
次に平面と直線の関係を見ていこう。
まず平面のなかに直線が含まれるという場合がある。
逆に平面に全く直線が触れることがない時もある。
この時は平面と直線が平行だという。
そして平面を直線が突き抜けている、
直線が平面に交わっているときがある。
この時平面と直線が垂直であるという状態もありうる。
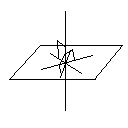
さて平面と直線が垂直というのは空間内においてどのようなことをさすのか。
直線lと平面Aが交わっている。直線lと平面Aの交点をHとする。
平面A上の任意の点P(点Hは除く)と点Hを通る直線PHを引くと、
いかなる場合もPHと直線lは垂直になった。
この時直線lと平面Aは垂直であるという。
最後に直線と直線、平面と直線ときたら、次は平面と平面の関係。
これは交わるか(交わるときは垂直も考えられる)平行かのどちらかである。
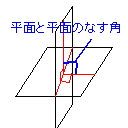
交わるときは二平面は一つの直線を共有する。
またその共有する直線lとその直線上のある点Pにおいて、
二つの平面上に点Pを通り直線lに垂直な直線PX、
PYをひくとき∠XPYがその二平面のなす角という。
この角度が90°の時二平面は垂直であるという。
さてこれで空間内の基本的な位置関係は学んだが、
これに関する問題というと非常にまぎらわしい問題が多い。
というのも垂直や平行という言葉がやたら問題文中に出てきて、
最終的に～と～は垂直かどうか、といったことを聞いてくるような問題があるからだ。
これはもう各自の頭にどれだけ忠実に問題文にかかれている図形を思い描けるかに
かかっているといっても過言でない。普段から頭は柔らかくしておこう。
ではまたちょっと違う話に移って行こう。
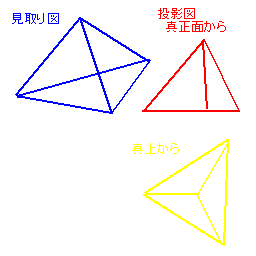
普段皆が見るような問題に出てくる立体は
見取り図というかきかたのものだろう。
だいたい斜め上あたりから見たままをかいたやつで
全体がどんな形になっているのかを知るのに適している。
しかし、世の中には別にかわった立体の書き方があって、
それが投影図と展開図である。
まず投影図から。
これは真っ正面から見た図、真上から見た図と
勝手に図形の正面真上を決めて
その方向から見たままをかく方法。
あまり複雑な図形だと見取り図ではかききれないこともあり、
そういうときにはこの投影図を使う。
この投影図を使った問題としては投影図から見取り図をかく、
見取り図から投影図をかく、の二通りがある。
いずれにしても自分のかいた答えがもとの見取り図なり
投影図なりにきちんと見えるか確かめること。
(このきちんと見えるというのは長さよりも形についていっている)
次に展開図。これはみな知っていると思う。
特にさいころの展開図は有名だ。
一つの立体があるとき、その立体の中身が空っぽだと思って
立体の辺を切っていくとできる図形、
逆にそれを組み立てると立体になる図形のことである。
この展開図を使った問題としては、
展開図をかきなさいとか展開図をもとに
見取り図を書きなさいという問題よりは、
展開図を問題を解く途中に使うという形の問題が多い。
例えばとある立体の二点を糸を結ぶとき糸が
最短になるにはどの点を通っていけばよいか、
というようなことを聞かれたとき。
これはその立体の展開図をかきその二点を結ぶ線分をかけば、
それが最短の糸の経路となるから、どの点を通るかはすぐに分かる。
注意としては展開図で二点を結ぶ線分を引こうとしたら途中で
途切れちゃったということがない様に。
きちんと途切れない線分が引けるように展開図をかくことが重要。
例を見ればわかりやすいと思う。
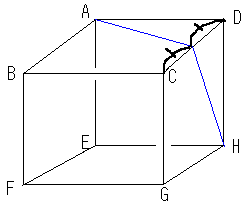
(例)上の立方体において点Aから点Gにかけて糸を辺CD上を経て
立方体の外側を通って結ぶようにしたい。
その時の糸の経路を見取り図の上にかけ。
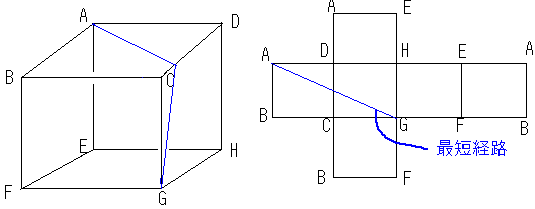
上のように展開図をかいてAGを線分を引けば辺CDの中点を通ることが分かる。
(二点を結ぶのに最短なのは線分だから)これをもとに答えをかくと上のようになる。
さてこの空間図形のページの最後の項目に入ろう。立体の切断である。
だいたいの問題は｢この立体のうち3点～～～を通るように切断するとき、
切断面のかたちはどうなるか｣といったものだが、使う知識は二つ。
同じ平面上にあり交わらない二直線は平行 同じ平面上にあり平行でない二直線は交わる
この二つである。ちなみ注意して欲しいのはこの二つに共通して出てくる同じ平面上
ということを考えるとき、この平面を接断面だと思ってほしい。
例を挙げよう。
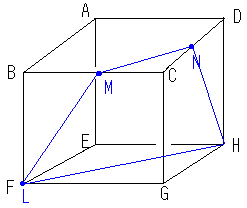
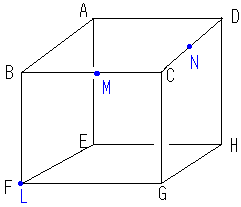(例)左の立方体を3点L、M、N(M,Nは
それぞれ辺の中点)を通る平面で切断するとき、
切断面はどのような形になるか。見取り図に図示しろ。
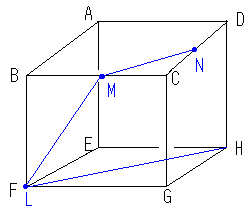
まず同じ面にあるLM,MNを結ぶ。
そして｢同じ平面上にあり交わらない二直線は平行｣ということをもとに、
MNとLから伸びる切り口の辺は平行だと思われる。
（なぜなら、MNがある面ABCDとLから伸びる切り口の辺が
あると思われる面EFGHは 平行で交わらないからである。）
よってLからMNに平行な直線を引くとHにつながる。
あとはHとNをつなげれば終わり。
さてこれで空間図形のページは終わり。大切なのは頭の柔らかさ。頭を大事にしていこう。