三平方の定理

三平方の定理は別名ピタゴラスの定理とも呼ばれ、
非常に有名な定理である。
数学の授業やこのページを見る前にすでに知っている人もいるかも知れないが、
そういう人もとりあえず確認の意味でも見ていこう。

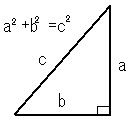三平方の定理は、直角三角形ABCがあり、�輸BC=90°のとき、
AC²=AB²+BC²
という関係が成り立つことを言う。
また逆にとある三角形の一番長い辺の二乗が残りの
二辺の二乗の和に等しいとき、
その三角形は一番長い辺を斜辺とする直角三角形であるということができる。
この定理は様々な証明の仕方があるがここでは紹介しない。
どうしても知りたいという人は、
教科書なり参考書なりを見てくれ。問題を解くにあたっては
上の関係が成り立つということさえ知っていれば十分である。

そして、三平方の定理を使うことで様々な線分の長さをしることができる。
例えば接線の長さ。点Pから円Oに引いた接線の長さlは点Pと円Oの中心点Oとの距離をd、
円Oの半径をrとおけば
l=�票d²-r²]
と計算できる。また二つの円があるときの共有する接線の長さも知ることができる。
上の図の�@においては
l=�票d²-(r-r')²]
上の図の�Aにおいては
l=�票d²-(r+r')²]
で計算できる。とにかく直角の図形が出てきたら何でも三平方の定理を使えるのである。


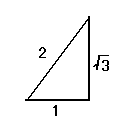
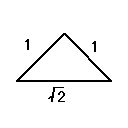
また、ここで直角三角形の中でも特殊なものを見てみよう。
上の図の�@�Aはいずれも皆よく知っているはずの三角定規の形である。
二種類の三角定規は上のような角度を持っていて、
かつ辺の比も上の図にあるように1:1:�票2]、1:2:�票3]である。
この直角三角形にある30°、60°、45°などの角度が問題の図形に出てきたとき、
この直角三角形を思い描いて、1:1:�票2]、1:2:�票3]という比を用いることもあるので
これは覚えてしまおう。

三平方の定理を使うのは図形の話ばかりでなく、
座標上の点と点の長さを計算するときなどにも使うものでもある。
また純粋に図形としての問題の中では円と絡み合わせてだしてくるケースもあるので
（なにしろ円という図形には弦や接線などにいくらでも直角の角がでてくるから）
円の性質についてもよく理解しておこう。