恾宍偺惈幙
偙傟偐傜條乆側栤戣傪夝偔偵偁偨偭偰抦偭偰偍偔傋偒庡側恾宍偺惈幙傪妛傇偺偑
偙偙偺儁乕僕偱偁傞丅恾宍偺栤戣偵尷傜偢側偐偵偼戙悢宯偺嵗昗偵偍偄偰傕梡偄傞偙偲傕偁傞偺偱丄
傛偔妎偊偰偍偙偆丅
傑偢丄懳捀妏偺愢柧偐傜丅
偙傟偼傛偔抦偭偰偄傞偲巚偆偑擇捈慄偑岎傢偭偰偄傞偲偒丄岦偐偄崌偆妏偺戝偒偝偑摍偟偄丅
傑偨摨埵妏傕暯峴慄偺偍偐偘偱摍偟偄
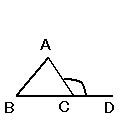 師偵嶰妏宍偵偮偄偰丅 師偵嶰妏宍偵偮偄偰丅
嶰妏宍偺撪妏偺崌寁偑180亱偱偁傞偙偲偼抦偭偰偄傞偩傠偆丅
偙傟偼暯峴慄傪傂偄偰暯峴慄偺摨埵妏偑摍偟偄偙偲傪梡偄偰徹柧偱偒傞丅
傑偨丄嶰妏宍偺堦偮偺奜妏偼丄奜妏偲怗傟側偄嶰妏宍偺巆傝擇偮偺妏偺
崌寁偵摍偟偄丅忋偺恾偱尵偆偲丄嚄ACD=嚄ABC+嚄BAC偱偁傞丅
偲偄偆偺傕偳偪傜傕忋偺恾偺応崌180亱-嚄ACB偱昞傢偝傟傞偐傜偱偁傞丅
偱偼懡妏宍偺撪妏偺榓偼偄偔偮偩傠偆偐丅
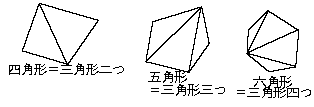
巐妏宍偵偍偄偰偼恾偺傛偆偵嶰妏宍擇偮偵暘妱偱偒傞偐傜360亱偱偁傞偙偲偑暘偐傞丅
屲妏宍偵偍偄偰偼偳偆偐丅恾偺傛偆偵嶰妏宍3偮偵暘妱偱偒傞偐傜撪妏偺榓偼540亱丅
偱偼榋妏宍偼丠恾偺傛偆偵嶰妏宍4偮偱偒傞偐傜撪妏偺榓偼720亱丅傕偆婥晅偄偨偩傠偆偐丅
堦偮妏偑憹偊傞偛偲偵撪妏偺崌寁偑180亱憹偊偰偄傞偺偱偁傞丅
偙傟傪幃偱昞傢偡偲丄n妏宍偵偍偄偰撪妏偺榓偼丄
180(n-2)
偲昞傢偣傞丅偪側傒偵媡偵懡妏宍偺奜妏偺榓偼壗妏宍偩傠偆偲360亱偵側傞丅
側偤偩偐偼偄偊傞偑愢柧偑挿偔側傞偺偱婥偵側傞恖偼嶲峫彂側傝壗側傝偱挷傋偰偔傟丅
奜妏偺榓偑360亱偵側傞偙偲傪抦偭偰偝偊偄傟偽栤戣偼側偄丅
 偱偼嵟屻偵徹柧偵偮偄偰怗傟偰偍偙偆丅
偙偺徹柧偲偄偆傕偺彫妛峑偺嶼悢偵偼側偐偭偨傕偺偱傛偆偼乣偑惓偟偄丄
娫堘偭偰偄傞偲偄偆偙偲傪偒偪傫偲愢柧偡傞傕偺偲巚偭偰偔傟偰偄偄丅
偨偩丄寢峔偟偭偐傝偐偐側偄偲尭揰偵側傞偐傜拲堄丅堦偮椺傪嫇偘偰傒傛偆丅
(椺)忋偺恾偺傛偆偵慄暘AD偑偁傝丄AC=BD偺偲偒丄AB=CD傪徹柧偟傠丅
AB=AD-BD ゥゥゥ嘆
CD=AD-AC
偝傜偵AC=BD側偺偱
CD=AD-BD ゥゥゥ嘇
傛偭偰嘆嘇傛傝
AB=CD
仩
暥偲暥丄幃側偳傪尨場偲寢壥偲偟偰偮側偘傞愙懕帉側偳偼備偊偵丄偟偨偑偭偰丄傛偭偰丄
側偳偺尵梩傪巊偄丄偝傜偵愙懕帉偺戙傢傝偵偙傟傜偺尵梩偲摨偠堄枴傪傕偮婰崋亪傪巊偭偨傝偡傞丅
偨偩偙偺婰崋偼懠偵尵梩傪巊傢側偄偲偒(忋偺椺偩偲@嘇傛傝苽羵綄緱t傪偮側偘側偄偲偒)
扨撈偱巊傢傟傞丅傑偨寢峔徹柧偺嵟屻偺曽偺廳梫側強偱巊傢傟傞丅
偦偟偰嵟屻偺仩偺儅乕僋偼貣緩I傢傝饡\傢偡婰崋偱偁傞丅
徹柧偺嵟屻偵偼貣緩I傢傝茠紣趶憘瓊﹣A
偙傟偲摨堄媊偺仩ˉ//側偳偺婰崋傪巊偆曽朄偑偁傞偑丄
偄偢傟偐傪彂偄偰偍偐側偄偲尭揰懳徾偵側傞偐傜梫拲堄丅
傑偨偙偺偁偲傕徹柧偲偄偆偺偼弌偰偔傞偑丄壗偺徹柧偐偵傛偭偰徹柧偺彂偒曽偵偁傞
掱搙婯懃偑偁傞応崌偑偁傞偑丄偦傟偼昁梫偵側偭偨帪揰偱妛傫偱偄偗偽傛偄丅
尰帪揰偱偼摿偵懠偵拲堄偡傋偒偙偲偼側偄丅
偱偼嵟屻偵徹柧偵偮偄偰怗傟偰偍偙偆丅
偙偺徹柧偲偄偆傕偺彫妛峑偺嶼悢偵偼側偐偭偨傕偺偱傛偆偼乣偑惓偟偄丄
娫堘偭偰偄傞偲偄偆偙偲傪偒偪傫偲愢柧偡傞傕偺偲巚偭偰偔傟偰偄偄丅
偨偩丄寢峔偟偭偐傝偐偐側偄偲尭揰偵側傞偐傜拲堄丅堦偮椺傪嫇偘偰傒傛偆丅
(椺)忋偺恾偺傛偆偵慄暘AD偑偁傝丄AC=BD偺偲偒丄AB=CD傪徹柧偟傠丅
AB=AD-BD ゥゥゥ嘆
CD=AD-AC
偝傜偵AC=BD側偺偱
CD=AD-BD ゥゥゥ嘇
傛偭偰嘆嘇傛傝
AB=CD
仩
暥偲暥丄幃側偳傪尨場偲寢壥偲偟偰偮側偘傞愙懕帉側偳偼備偊偵丄偟偨偑偭偰丄傛偭偰丄
側偳偺尵梩傪巊偄丄偝傜偵愙懕帉偺戙傢傝偵偙傟傜偺尵梩偲摨偠堄枴傪傕偮婰崋亪傪巊偭偨傝偡傞丅
偨偩偙偺婰崋偼懠偵尵梩傪巊傢側偄偲偒(忋偺椺偩偲@嘇傛傝苽羵綄緱t傪偮側偘側偄偲偒)
扨撈偱巊傢傟傞丅傑偨寢峔徹柧偺嵟屻偺曽偺廳梫側強偱巊傢傟傞丅
偦偟偰嵟屻偺仩偺儅乕僋偼貣緩I傢傝饡\傢偡婰崋偱偁傞丅
徹柧偺嵟屻偵偼貣緩I傢傝茠紣趶憘瓊﹣A
偙傟偲摨堄媊偺仩ˉ//側偳偺婰崋傪巊偆曽朄偑偁傞偑丄
偄偢傟偐傪彂偄偰偍偐側偄偲尭揰懳徾偵側傞偐傜梫拲堄丅
傑偨偙偺偁偲傕徹柧偲偄偆偺偼弌偰偔傞偑丄壗偺徹柧偐偵傛偭偰徹柧偺彂偒曽偵偁傞
掱搙婯懃偑偁傞応崌偑偁傞偑丄偦傟偼昁梫偵側偭偨帪揰偱妛傫偱偄偗偽傛偄丅
尰帪揰偱偼摿偵懠偵拲堄偡傋偒偙偲偼側偄丅
丂
|

師偵嶰妏宍偵偮偄偰丅
偱偼嵟屻偵徹柧偵偮偄偰怗傟偰偍偙偆丅 偙偺徹柧偲偄偆傕偺彫妛峑偺嶼悢偵偼側偐偭偨傕偺偱傛偆偼乣偑惓偟偄丄 娫堘偭偰偄傞偲偄偆偙偲傪偒偪傫偲愢柧偡傞傕偺偲巚偭偰偔傟偰偄偄丅 偨偩丄寢峔偟偭偐傝偐偐側偄偲尭揰偵側傞偐傜拲堄丅堦偮椺傪嫇偘偰傒傛偆丅 (椺)忋偺恾偺傛偆偵慄暘AD偑偁傝丄AC=BD偺偲偒丄AB=CD傪徹柧偟傠丅 AB=AD-BD ゥゥゥ嘆 CD=AD-AC 偝傜偵AC=BD側偺偱 CD=AD-BD ゥゥゥ嘇 傛偭偰嘆嘇傛傝 AB=CD 仩 暥偲暥丄幃側偳傪尨場偲寢壥偲偟偰偮側偘傞愙懕帉側偳偼備偊偵丄偟偨偑偭偰丄傛偭偰丄 側偳偺尵梩傪巊偄丄偝傜偵愙懕帉偺戙傢傝偵偙傟傜偺尵梩偲摨偠堄枴傪傕偮婰崋亪傪巊偭偨傝偡傞丅 偨偩偙偺婰崋偼懠偵尵梩傪巊傢側偄偲偒(忋偺椺偩偲@嘇傛傝苽羵綄緱t傪偮側偘側偄偲偒) 扨撈偱巊傢傟傞丅傑偨寢峔徹柧偺嵟屻偺曽偺廳梫側強偱巊傢傟傞丅 偦偟偰嵟屻偺仩偺儅乕僋偼貣緩I傢傝饡\傢偡婰崋偱偁傞丅 徹柧偺嵟屻偵偼貣緩I傢傝茠紣趶憘瓊﹣A 偙傟偲摨堄媊偺仩ˉ//側偳偺婰崋傪巊偆曽朄偑偁傞偑丄 偄偢傟偐傪彂偄偰偍偐側偄偲尭揰懳徾偵側傞偐傜梫拲堄丅 傑偨偙偺偁偲傕徹柧偲偄偆偺偼弌偰偔傞偑丄壗偺徹柧偐偵傛偭偰徹柧偺彂偒曽偵偁傞 掱搙婯懃偑偁傞応崌偑偁傞偑丄偦傟偼昁梫偵側偭偨帪揰偱妛傫偱偄偗偽傛偄丅 尰帪揰偱偼摿偵懠偵拲堄偡傋偒偙偲偼側偄丅