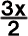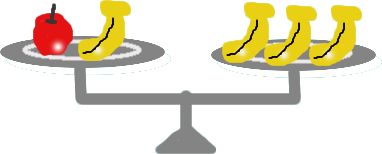
等式の変形

りんご１個とバナナ１本
バナナ３本

上の天秤はつりあっています。
りんご１個はバナナ何個分かな？？


左の皿のバナナ１本をとると右の皿の方が重くなるよね。


つりあうためには右の皿からも同じ分だけバナナをとってあげよう。

これでりんご１個分はバナナ２本分ということがわかるね。

これを
りんご１個 Ａグラム
バナナ１本 Ｂグラムとして式にあらわしてみよう。

左の皿
右の皿
Ａ＋Ｂ
＝
３Ｂ
Ａ＋Ｂ−Ｂ
＝
３Ｂ−Ｂ
Ａ
＝
２Ｂ

この式からりんごの重さはバナナの２倍だということがわかった。
このように、Ａ＝□　の形になおすことを　Ａについて解く　という。

注意！
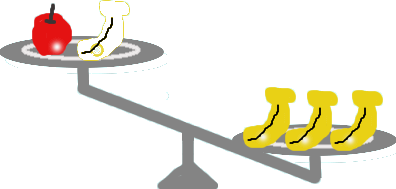
いままで右の皿、左の皿といっていたけど式の中 では右辺、左辺というよ。
右辺＝左辺


同じように、今度はｙについて解いてみよう。
つまりｙ＝□の形にしてみよう。
３ｘ−２ｙ
＝ １０
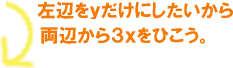３ｘ−２ｙ−３ｘ
＝ １０−３ｘ
　―２ｙ
＝ １０−３ｘ
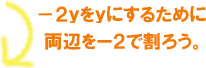−２ｙ÷（−２）
＝ （１０−３ｘ）÷（−２）
ｙ
＝
−５＋


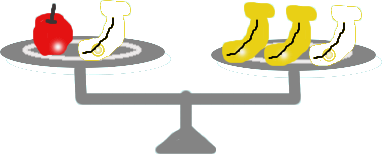
たしざん、ひきざん、わりざん、かけ ざんをする時には右辺にも左辺にも同 じ分だけ計算するようにしよう。
イコール（＝）で結ばれている式を等式というけれど、 これはいま説明したように天秤みたいなものなんだよ。 だから、同じ分だけたしたり、ひいたりしてあげないと いけないのだ。


前のページ
次のページ

「式の計算」へ戻る　用語集