| 今度は | y=-x2 | のグラフについて考えてみよう。 |
| y=-x2 | のグラフをかくために、xの値に対応するyの |
| 値について考えよう。 | |
| x | ・・・ |
|
|
|
|
|
|
|
・・・ |
| y | ・・・ |
|
|
|
|
|
|
|
・・・ |
| y=x2 | のグラフと同じように、式を満たすxとyの値の |
|
組を座標にとっていくと、点が隙間なくうまって下のよ
うな滑らかな曲線になるんだ。
|
|
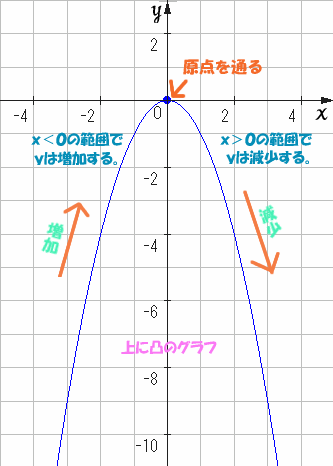
| y=-x2 | のグラフの特徴 |
 |
|
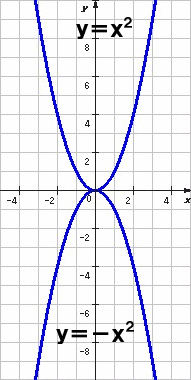
| この | y=-x2 | のグラフと | y=x2 | のグラフを見比べると、 |
| x軸に対して線対称なグラフであることがわかるね。 | ||||

|

|
|
|
|