|
|
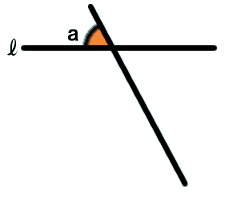
���s���̓��ʊp�͓������B
�܂��A���ʊp�����������͕��s�B
|
|
 |
|
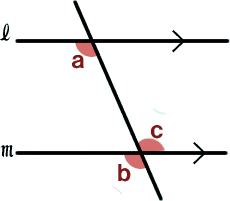
���s���̍��p�͓������B
�܂��A���p�̓��������͕��s�B
|
|
 |
|
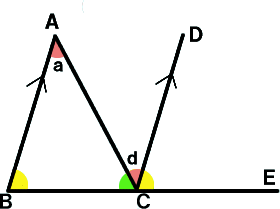
�O�p�`�̓��p�̘a�͂P�W�O���ł���B
�ڂ`�{�ڂa�{�ڂb���P�W�O��
|
|

|
|
�O�p�`�̊O�p�ׂ͗荇��Ȃ��Q��
�̓��p�̘a�ɓ������B
�ڂ`�̊O�p���ڂa�{�ڂb
|
|
 |
|
�O�p�`�̍�������
|
|
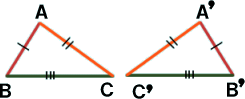 |
|
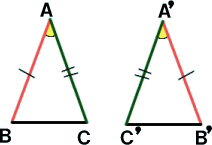
�Q�ӂƂ��̊Ԃ̊p�����ꂼ�ꓙ�����B
|
|
 |
|
�P�ӂƂ��̗��[�̊p�����ꂼ�ꓙ�����B
|
|
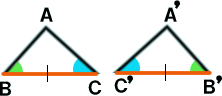 |
|

