�~���p�ƒ��S�p
�藝
�P�̌ʂɑ���~���p�͏�Ɉ��ŁA���̌ʂɑ��钆�S�p��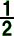 �ɓ���
���B �ɓ���
���B
|
|
�_�o�������ɂƂ��Ă�
�ڂ`�o�a�̑傫���͕ς��Ȃ��B
|
|
|
|
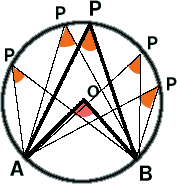
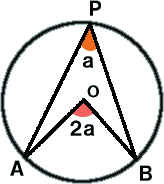
�~���p�͏�ɒ��S�p�̔����B
|
|
|
|
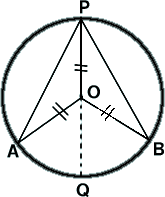 |
�ؖ�
|
�����n�`�A�n�o�A�n�a�͉~�̔��a�Ȃ̂ŁC
�n�`���n�o���n�a
�n�`���n�o������A���n�o�`�͓ӎO�p�`�B
�ӎO�p�`�̒�p�͓������̂ŁA
�ڂn�`�o���ڂn�o�`���ڂ��@�Ƃ����B
�O�p�`�̊O�p�̒藝���A
|
�ڂ`�n�p
|
��
|
�ڂn�`�o�{�ڂn�o�`
|
|
��
|
�ڂ��{�ڂ�
|
|
��
|
�Q�ڂ�
|
���l�ɁA�ڂn�a�o���ڂn�o�a���ڂ��@�Ƃ����ƁA
�ڂp�n�a���Q�ڂ�
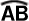 �ɑ���~���p �ɑ���~���p
�ڂ`�o�a���ڂ��{�ڂ�
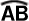 �ɑ��钆�S�p �ɑ��钆�S�p
|
�ڂ`�n�a
|
��
|
�Q�ڂ��{�Q�ڂ�
|
|
��
|
�Q�i�ڂ��{�ڂ��j
|
����āA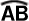 �̉~���p�͒��S�p�� �̉~���p�͒��S�p��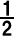 �ɂȂ��Ă���B �ɂȂ��Ă���B
|
|

