$ここで算数や数学を学びます$

様々な三角形、四角形

このページでは様々な三角形や四角形、二等辺三角形や直角三角形、平行四辺形などについて
学んでいく。が、その前にまず三角形の合同から見ていこう。

合同というのは「形も大きさも同じ」ということである。言い換えると二つの図形があったとき、
一方の図形を回転したり、裏返したり、平行移動したりするともう一方の図形に重ねることが
できるということである。→平行移動動画
非常に単純なことであるが、問題としては、「何々と何々が合同であるということを証明せよ」という形のものが多い。
そこでこの手の問題を解くのに最も使われる三角形の合同条件を見てみよう。
①三辺の長さが等しい

②２辺の長さとその挟む角の大きさが等しい

③一辺の長さとその両端の角の大きさが等しい

これらのいずれかが成り立てば二つの三角形が合同であるといえるのである。
ちょっと考えれば分かると思うが、コンパスと定規、分度器を使って三角形をかくとき、
・三辺の長さ
・２辺の長さとその挟む角
・一辺の長さとその両端の角が与えられれば
、一通りの三角形しかかくことができない。
だから先の三つが合同条件となりうるのである。
また二つの三角形が合同である事を証明するとき、
その三角形が直角三角形だとまた別の合同条件ができる。
Ⅰ斜辺と一鋭角が等しい
Ⅱ斜辺ともう一辺が等しい
この二つのうちどちらかが成り立てばその二つの直角三角形は合同といえる。
Ⅰの条件「斜辺と一鋭角が等しい」は三角形の合同条件の③「一辺の長さとその両端の角」と同じ事を言ってる。
なぜなら直角と一鋭角が分かれば残りの角の大きさも分かり、斜辺とその両端の角が与えられるのと同じである。
Ⅱの条件は実際作図してみると二つ三角形ができるがこの二つは合同なので結局一通りの三角形しか
できないのである。(作図の動画）

さてここで直角三角形が出てきたついでに直角三角形の性質をみていこう。
といっても知っておくべきことはそれほどない。
まず90°の角に触れていない辺のことを斜辺といい、
直角三角形の三辺の中では一番長いということ。
そして直角三角形は一つの角が90°であり、
残りの二つの角の合計が90°であること。
この二つが分かっていればよい。
では別の三角形、二等辺三角形においてはどうか。
二等辺三角形の定義は二辺の長さが等しい
三角形のことで、定理としては、
・二等辺三角形において二つの角の大きさが等しい。
・二等辺三角形の頂角(等しい二つの角を除いたもう一個の角)から
底辺(等しい二つの角を両端に持つ辺）におろした垂線は底辺を二等分する
などがある。

さてここで出てきた定義、定理という言葉について。
定義というのはとある物事がいかなる物かをきちんと述べたもの。
物事の本質的な意味と思ってくれればよい。
例えば二等辺三角形は二つの角が等しいが、二等辺三角形は二つの角が等しい三角形を
意味するかというとそうではなく、二つの辺が等しい三角形を意味する、という具合である。
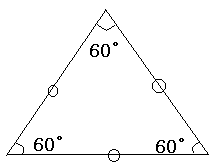さらにもう一つの特別な三角形としては正三角形がある。
これは三つの辺の長さが等しい三角形で、
三つの角が皆60°で等しいという性質を持つ。
また正三角形は二等辺三角形の一種でもあるので、
正三角形は先にあげた二等辺三角形の性質を全て持っている。
これで三角形はおしまい。

次に四角形についてみていこう。
まず向かい合う一対の辺が平行な図形を台形という。
さらに二対の辺が平行な図形を平行四辺形という。
平方四辺形のうち四辺全てが同じ長さのものをひし形、四つの角が
全て90°のものを長方形という。
そして、平方四辺形のうち四辺が全て同じながさで、
四つの角が全て90°のものを正方形という。
これはもう小学校で習っているだろう。この関係を図に表わすと下のようになる。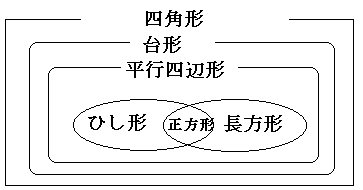
ここで注意してほしいのは、内側にあるものは
外側の図形の一種であるということである。
例えば平行四辺形は台形である。
正方形はひし形であり、長方形であり、
平行四辺形であり、台形でもあり、そしてこれら
四つの図形の性質を全て持っている図形である。ではここで平行四辺形の性質を見ていこう。
平行四辺形の定義は
｢2組の対辺(向かい合う辺のこと)が
それぞれ平行な四角形｣である。
定理としては
・向かい合う辺の長さが等しい
・向かい合う角の大きさが等しい
・平行四辺形の二つの対角線はたがいを二分する
(対角線の交点は二つの対角線それぞれの
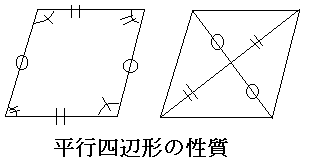中点である) などがある。平行四辺形の問題としては
｢この四角形が平行四辺形であることを証明しなさい｣という
問題が結構出る。これを解くには一体四角形が
平行四辺形である条件とは何かを知っていなければ
ならない。
次の五つがある。
・二組の対辺が平行である
・二組の対辺の長さが等しい
・二組の向かい合う角の大きさが等しい
・二つの対角線が互いを二等分する
・一組の対辺が平行でしかも長さが等しい
この五つのいずれかを証明したらその四角形は
平行四辺形だといえる。この手の問題は
この平行四辺形の性質だけを知っていたら解けるかといったらそうでもなく、三角形の合同を
利用してとくという問題もあるから、今までの項目をよく理解しておこう。

さて図形の性質を理解したら次は面積を見ていこう。
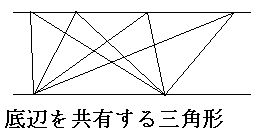
左の図をみてほしい。二本の平行な直線の間に
たくさんの底辺を共有する三角形が描かれているが、
これらの三角形すべての面積は等しい。
三角形の面積を求める式は (底辺)×(高さ)×1/2 で
あった。上の三角形は底辺は共有しているので底辺は
全て等しい。高さはどうかとみると直線lと直線mは
平行なので二直線間の距離(=三角形の高さ)は常に一定。
だから上の三角形の面積は全て面積がおなじである。
この性質を使うと等積変形という作業ができる。
これは面積を求める問題などで、とある三角形を
平行線を引いて形は違えど面積は同じ三角形を別に作ってしまうことである。
チェックテストでこれを使って解く問題を一つあげておく。
他に使う性質といえば
・合同な図形は面積が等しい
・平行四辺形の対角線は平行四辺形の面積を二等分する。
ぐらいである。ここで注意するのは平行四辺形というのはひし形、長方形、正方形を含んでいることである。
二番目の性質を使うときに思い起こして欲しい。