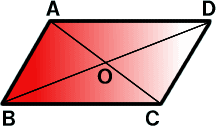
平行四辺形を2本の対角線の交点を中心に180°回転させてみると
 |
⇒
|
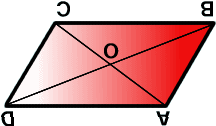 |
もとの図形にピッタリ重なりますね。
このようにある点Oを中心として
「180°回転させるともとの図形にピッタリ重なる図形」
を点対称な図形といいます。
この時、点Oを対称の中心といいます。
点Oを180°回転したとき
|
重なり合う点を
|
対応する点
|
|
|
重なり合う辺を
|
対応する辺
|
|
|
重なり合う角を
|
対応する角
|
といいます。
|
|
|
左の図の場合
|
対応する点は
|
点A
|
と
|
点D
|
|
点B
|
と
|
点C
|
|
←画像をクリック!
|
|
対応する辺は
|
辺AB
|
と
|
辺DC
|
|
←画像をクリック!
|
|
対応する角は
|
∠A
|
と
|
∠D
|
|
∠B
|
と
|
∠C
|
|
←画像をクリック!
|
|
点対称な図形の性質
対応する2点を結ぶ線分は対称の中心を通る。
対称の中心から対応する2点までの距離は等しい。
|
|

