四角形の内角の和を調べたのと同じように,五角形、六角形・・・を考
えていくと、
|
四角形
|
五角形
|
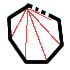
六角形
|
七角形
|
・・・
|
n角形
|
・・・
|
|

|

|

|

|
|

|
|
|
頂点の数
|
4
|
5
|
6
|
7
|
・・・
|
n
|
・・・
|
一つの頂
点から引
ける対角
線の数
|
1
|
2
|
3
|
4
|
・・・
|
n−3
|
・・・
|
対角線を
引いてで
きる三角
形の数
|
2
|
3
|
4
|
5
|
・・・
|
n−2
|
・・・
|
(nは自然数)
四角形の場合は、1つの頂点から対角線を引くと二つの
三角形ができたので、
|
 |
五角形の場合も同じように考えると、3つの三角形がで
|
 |
|
|
 |
|
n角形の場合を考えると、一つの頂点から対角線を引い
|
 |
|

