|
|
ڈط–¾
|
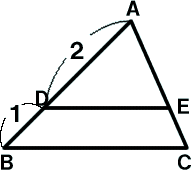
‚ـ‚¸‚حپ¢‚`‚a‚b‚ئپ¢‚`‚c‚d‚ھ‘ٹژ—‚إ‚ ‚邱‚ئ‚ًژ¦‚»‚¤پB
پ¢‚`‚a‚b‚ئپ¢‚`‚c‚d‚ة‚¨‚¢‚ؤ
‰¼’è‚و‚èپ@‚c‚d//‚a‚b
‚c‚d//‚a‚b‚¾‚©‚畽چsگü‚ج“¯ˆتٹp‚و‚è
پع‚`‚a‚bپپپع‚`‚c‚dپc‡@
پع‚`‚b‚aپپپع‚`‚d‚cپc‡A
‡@‡A‚و‚èپA‚Q‚آ‚جٹp‚ھ“™‚µ‚¢‚©‚çپ¢‚`‚a‚bپنپ¢‚`‚c‚d
‚Q‚آ‚جژOٹpŒ`‚ح‘ٹژ—‚إ‚ ‚é‚©‚ç‚»‚ꂼ‚ê‚ج•س‚ج”ن‚ح“™‚µ‚¢پB
‚آ‚ـ‚è
‚`‚cپF‚`‚aپپ‚`‚dپF‚`‚bپپ‚c‚dپF‚a‚b
‚`‚cپF‚c‚aپپ‚QپF‚P ‚و‚è
‚`‚cپF‚`‚aپپ‚QپF‚Rپپ‚`‚dپF‚`‚b
‚`‚dپF‚`‚bپپ‚QپF‚R‚¾‚©‚ç‚`‚dپF‚d‚bپپ‚QپF‚P
|

|
|
|