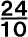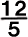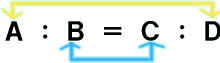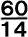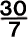| �O�p�`�̈�ӂɕ��s�Ȓ������Ђ������ɂł�������̔� �ɂ��čl���Ă������B |
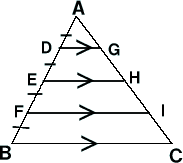
|
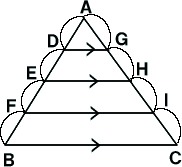
| ���ꂩ�牽�̔䂪�����Ȃ̂��O�p�`�̑� ���𗘗p���ďؖ������Ă������B |
|
|
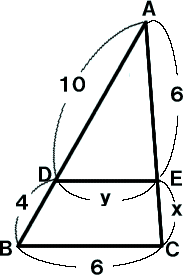
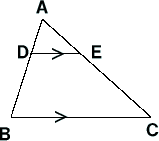
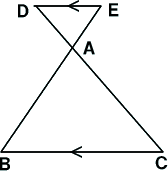
���`�a�b�ɂ����āA�_�c�A�d�����ꂼ���ӂ`�a�A�`�b��A�܂�
�͂��̉�����̓_�Ƃ���Ƃ����̂��Ƃ�������B
 |
|
����聄
�O�p�`�Ɣ�̒藝�𗘗p���Ă��Ƃ��̒l�����߂悤
|

|

|
|
|
|