|
�ڂ`�̓����Ƃa�b�Ƃ̌�_���c�Ƃ���B
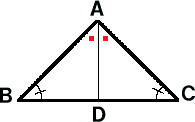
���`�a�c�Ɓ��`�b�c�ɂ�����
������@�ڂa���ڂb�@�@
�܂��A�ڂa�`�c���ڂb�`�c�@�A
�O�p�`�̓��p�̘a�͂P�W�O���ł��邩��
�@�A���@�ڂ`�c�a���ڂ`�c�b�@�B
�܂��A�`�c�͋��ʁ@�C
�A�B�C���@��ӂƂ��̗��[�̊p�����ꂼ��
����������
���`�a�c�߁��`�b�c
���@�`�c���`�b
|