相似な二つの図形の対応する辺の長さの比を相似比というよ。
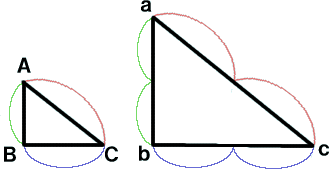
△ABCと△abcは辺の長さが2倍になっている。
|
(
|
△ABCの辺の長さを1とすると△abcの辺の長さは
2倍されていると考えることができるね!
|
)
|
合同な図形は相似比が1:1の相似な図形と考えることもできる。
2つの相似な三角形の相似比を調べよう。
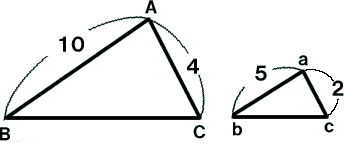
対応する辺の比を考えればよいから
|
AB:ab
|
=
|
AC:ac
|
|
10:5
|
=
|
2:1
|
|
4:2
|
=
|
2:1
|
つまり△ABCと△abcの辺の比は2:1
しかし、隣り合う辺の比についても考えてみると
ということができる。
 |
相似な図形は形が同じなので隣り合う辺
の長さの割合も変わることがないのだ。
|
AB:AC=5:2といえるよね。
ややこしいけど覚えておくと便利だよ!
|

