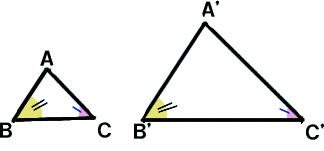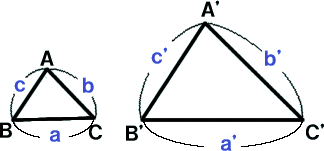
三角形の相似比
相似な三角形をかくにはどのような条件が必要だろうか？
一年生平面図形の三角形の作図で学んだことを覚えているかな？？
①３辺の長さ
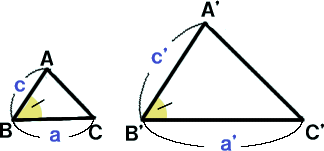
②２辺の長さとその間の角の大きさ
③１辺とその両端の角の大きさ
この３つのいずれかがわかれば三角形を作図することができたんだ。

相似な三角形を作るにはなにがわかっていればいいかこ れをもとに考えると…
①３辺の長さ ⇒ ①３組の辺の比
②２辺の長さとその間の角の大きさ ⇒ ②２組の辺の比とその間の角の大きさ
③１辺とその両端の角の大きさ ⇒ ③２つの角の大きさ

この３つのうちいずれかがわかっていれば相似な三角形を 作図することができる。
（この作図の場合は分度器を使ってもいいよ！）

また２つの三角形が相似であることを証明するための条件 について次のようにまとめることができる。

三角形の相似条件
２つの三角形は次のおのおのの場合に相似である。
①３組の辺の比が等しい。
ａ：ａ'＝ｂ：ｂ'＝ｃ：ｃ'
②２組の辺の比が等しくその間の 角がそれぞれ等しい。
ａ：ａ'＝ｃ：ｃ'　かつ　∠Ｂ＝∠Ｂ'
③２組の角がそれぞれ等しい。
∠Ｂ＝∠Ｂ'　かつ　∠Ｃ＝∠Ｃ'

前のページ
次のページ

「相似な図形」へ戻る　用語集