平行線と線分の比
直線が平行線と交わるときにできる線分の比について考えてみよう。

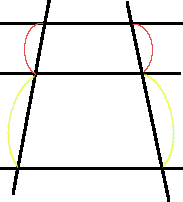
下の図を考えよう。平行な３つの直線ａ、ｂ、ｃに直線ｌ、ｍが交わっ ている。
ＡＢ：ＢＣ＝２：３ だけれど、 ＤＥ：ＥＦ の比はどうなっているかな？
点Ａから点Ｆを結ぶ線分を追加すると一気にわかるよ。
↓画像をクリック！
△ＡＣＦに注目しよう。
←画像をクリック！

ＢＧ//ＣＦより
ＡＢ：ＢＣ ＝ＡＧ：ＧＦ
＝２：３

△ＦＡＤに注目しよう。
←画像をクリック！

ＧＥ//ＡＤより
ＦＧ：ＡＧ ＝ＦＥ：ＥＤ
＝３：２
つまりＤＥ：ＥＦ＝２：３＝ＡＢ：ＡＣ

平行線と線分の比（まとめ）
いくつかの平行線に、２直線が
交わるとき、対応する線分の比
は等しい。



例題
平行線と線分の比の関係を利用してｘとｙを求めてみよう。

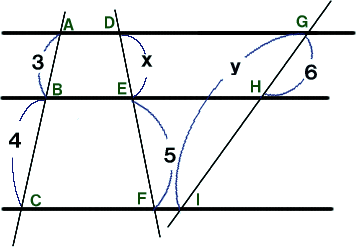
ｘを求めよう！
直線ａ、ｂ、ｃは平行だから、
３：４
＝ ｘ：５
４×ｘ
＝ ３×５
４ｘ
＝ １５
ｘ
＝ １５/４
ｙを求めよう！
直線ａ、ｂ、ｃは平行だから、
３：（３＋４）
＝ ６：ｙ
３：７
＝ ６：ｙ
３×ｙ
＝ ７×６
３ｙ
＝ ４２
ｙ
＝ １４

前のページ
次のページ

「相似な図形」へ戻る　用語集