|
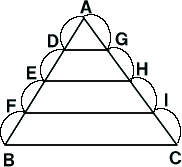
右の三角形を見てみよう。
点D、E、Fは辺ABを4等分するよう
においてある。
点G、H、Iは辺ACを4等分するよう
においてある。
線分DG、EH、FIは線分BCとどのよ
うな関係にあるだろうか??
|
 |
|
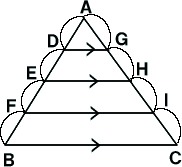
結論からいってしまうと
線分DG、EH、FIは線分BCと平行に
なっているんだ。
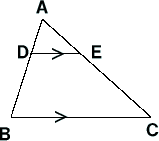
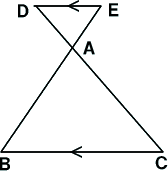
二つの辺をそれぞれ等しい辺にわけ
て、それぞれ対応する2点を結んで
できた線分は平行になるんだ。
|
 |
 |

|

|
|
|
|
