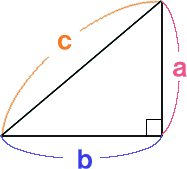
| 下の図のように直角三角形のそれぞれの辺を1辺とする正 方形P、Q、Rの面積にはどんな関係があるかな? |
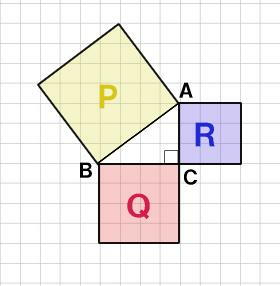
| 直角三角形の三辺の長さをa、b、cとすると、正方形Pの |
| 面積 | c2 | は | a+b | を1辺とする正方形の面積から4つの合 |
| 同な直角三角形の面積を引いたものと等しいよね。 |
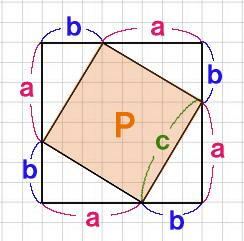 |
だから、正方形Pの面積は次のよう
に表せる。
|
|
このことから直角三角形の3辺の長さについて、3辺の長さを
|
| a、b、cとすると | c2=a2+b2 | という関係が成り立つ。 |
| この関係を三平方の定理またはピタゴラスの定理と言う。 |
|
| 三平方の定理は別の方法でも証明できるよ! |
|

|

|
|
|
|