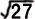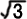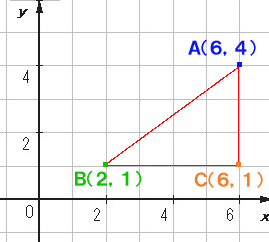
２点間の距離
２点、Ａ（６，４）、Ｂ（２，１）の距離を求めよう。
まず、点Ｃ（６，１）をと り、直角三角形ＡＢＣを作 る。
ＡＣ2＝４2−１2＝３2
ＢＣ2＝６2−２2＝４2
三平方の定理より、
ＡＢ2 ＝ ＢＣ2＋ＡＣ2
＝ ４2＋３2
＝ ２５
ＡＢ＞０なので
ＡＢ＝５
答　５




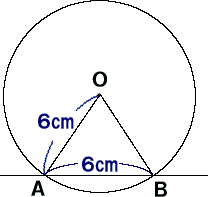半径６ｃｍの円０で弦ＡＢの長さが ６ｃｍのとき、中心０から弦ＡＢま での長さを求めよう。
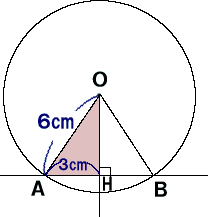まず、中心０から弦ＡＢに垂線を 引き、交点を点Ｈとしよう。
△ＯＡＨはＯＡを斜辺とする直角 三角形なので、三平方の定理よ り、
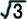
ＯＡ2
＝ ＡＨ2＋ＯＨ2
６2
＝ ３2＋ＯＨ2
−ＯＨ2
＝ ３2−６2
−ＯＨ2
＝ −２７
ＯＨ2
＝ ２７
ＯＨ＞０なので、
ＯＨ ＝
＝ ３
答　３


前のページ
次のページ

「三平方の定理」へ戻る　用語集