2 Grundy Numbers of chocolate bar
In this paper we study Grundy numbers of chocolate bar. For a general bar, the strategies seem complicated. We focus on bars that grow regularly in height. Let Difinition 2.1. 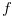 be a function that satisfies the following two conditions:
be a function that satisfies the following two conditions:
(i) 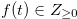 for
for 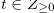 .
.
(ii) 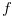 is monotonically increasing,i.e., we have
is monotonically increasing,i.e., we have 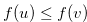 for
for 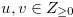 with
with 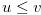 .
.
Definition 2.2. Let 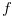 be the function that satisfies the conditions in Definition 2.1.
be the function that satisfies the conditions in Definition 2.1.
For 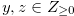 the chocolate bar will consist of
the chocolate bar will consist of 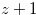 columns where the 0th column is the bitter square and the height of the
columns where the 0th column is the bitter square and the height of the 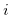 -th column is
-th column is 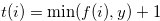 for i = 0,1,...,z. We will denote this by
for i = 0,1,...,z. We will denote this by 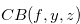 .
.
Thus the height of the 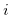 -th column is determined by the value of
-th column is determined by the value of 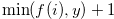 that is determined by
that is determined by 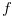 ,
, 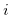 and
and 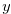 .
.
Example 2.1. Here are examples of chocolate bar games 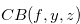 .
.

Figure 2.1 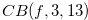
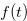
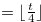
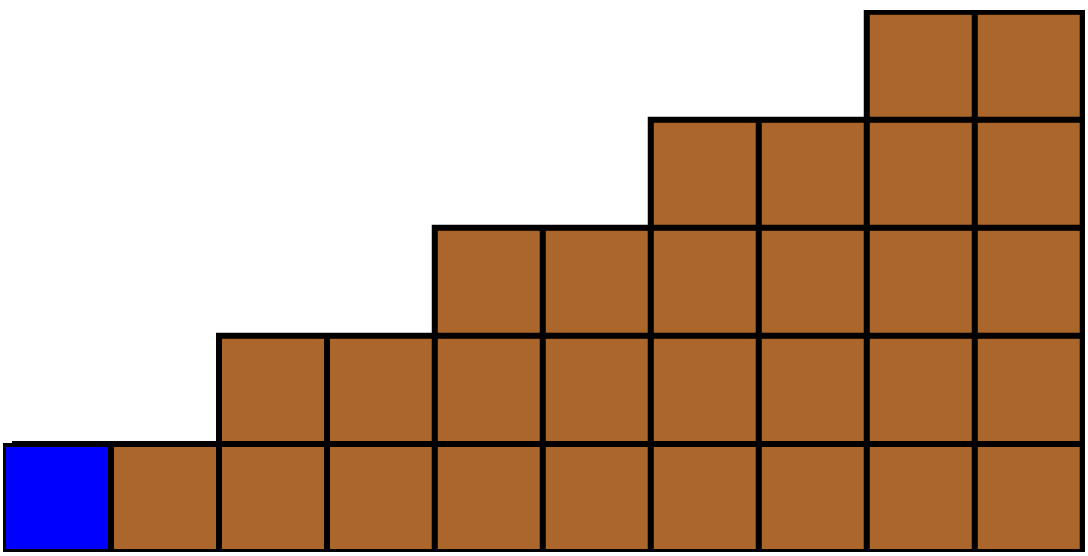
Figure 2.2 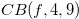
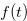
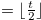

Figure 2.3 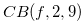
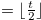

Figure 2.4 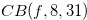
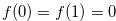 and
and 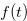
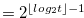 for
for 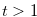 .
.
For a fixed function  , we denote the position of
, we denote the position of 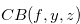 by coordinates
by coordinates 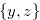 without mentioning
without mentioning 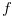 .
.
Example 2.4.
Here, we present four examples of coordinates of positions of chocolate bars when 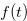
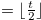 .
.
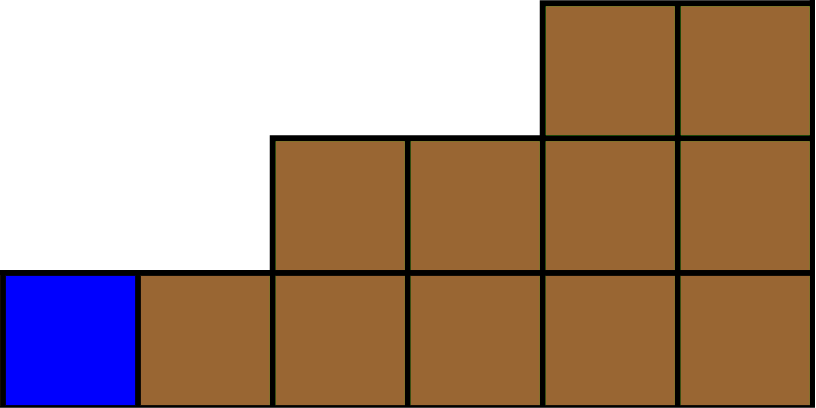
Figure 2.5. 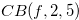
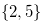
![]()
Figure 2.6. 
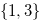
![]()
Figure 2.7. 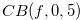
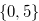
![]()
Figure 2.8. 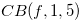
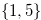
For a fixed function 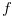 , we define
, we define 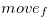 for each position
for each position 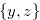 of the chocolate bar
of the chocolate bar 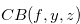 . This
. This 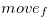 is a special case of
is a special case of 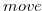 defined in Definition 1.4.
defined in Definition 1.4.
Definition 2.3.
For 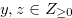 we define
we define
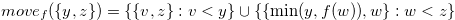 , where
, where 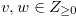 .
.
Example 2.3. Here, we explain about move when 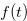
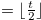 . If we start with the position
. If we start with the position 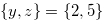 and reduce
and reduce 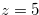 to
to 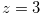 , then the y-coordinate (the first coordinate) will be
, then the y-coordinate (the first coordinate) will be 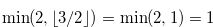 .
.
Therefore we have 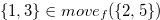 . It is easy to see that
. It is easy to see that 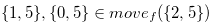 ,
, 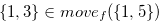 and
and 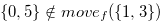 .
.