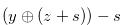4 A Chocolate Game 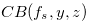 whose Grundy number is
whose Grundy number is 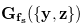
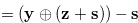 for a fixed natural number s
for a fixed natural number s
In the previous sections we studied the chocolate bar 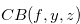 whose Grundy number is
whose Grundy number is 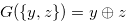 . The condition
. The condition 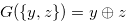 is very strong, so we modified it and get the condition that
is very strong, so we modified it and get the condition that 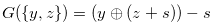 for a fixed natural number
for a fixed natural number 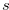 .
.
In this section we study a necessary and sufficient condition for a chocolate bar 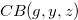 to have the Grundy number
to have the Grundy number 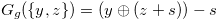 for a fixed natural number
for a fixed natural number 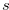 .
.
Example 4.1. By Lemma 3.1 and Theorem 3.2, the Grundy number of the chocolate bar in Figure 4.1 is
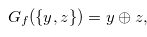 |
(4.1) |
where
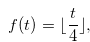 |
(4.2) |
but Theorem 4.1 (We prove this theorem later in this paper.) implies that the Grundy number of the chocolate bar in Figure 4.2 is
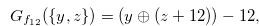 |
(4.3) |
where
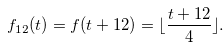 |
(4.4) |
Please look at the difference between (4.1) and (4.3), and the difference between (4.2) and (4.4).
It is easy to see that we get the chocolate bar in Figure 4.2 by moving the bitter part horizontally and cutting the chocolate bar in Figure 4.1 vertically. We present this method in Figure 4.3.
If we generalize this method, we can get a necessary and sufficient condition for a chocolate bar 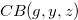 to have the Grundy number
to have the Grundy number 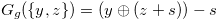 for a fixed natural number
for a fixed natural number 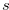 .
.

Figure 4.1. 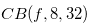
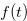
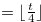

Figure 4.2. 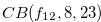
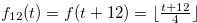
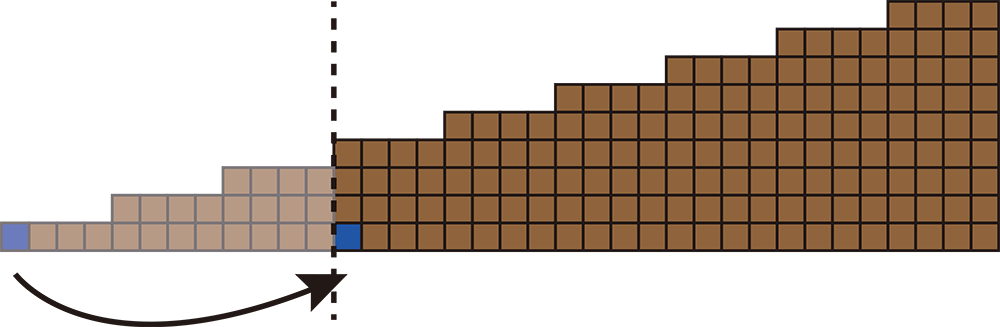
Figure 4.3.
As in Example 4. 1 we can make the chocolate bars that have the Grundy number 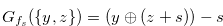 from the chocolate bar whose Grundy number is
from the chocolate bar whose Grundy number is 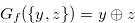 .
.
First, we study a sufficient condition.