1 Introduction
The original chocolate bar game [2] had a rectangular bar of chocolate with one bitter corner. Each player in turn breaks the bar in a straight line along the grooves and eats the piece he breaks off. The player who breaks the chocolate bar and eats to leave his opponent with the single bitter block (black block) is the winner.
The 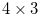 rectangular chocolate bar in Figure 1.1 is equivalent to the game of NIM with a heap of 3 stones and a heap of 2 stones. Here, 3 is the number of grooves above and 2 is the number of grooves to the right of the bitter square. Since the Grundy number of the game of NIM with a heap of
rectangular chocolate bar in Figure 1.1 is equivalent to the game of NIM with a heap of 3 stones and a heap of 2 stones. Here, 3 is the number of grooves above and 2 is the number of grooves to the right of the bitter square. Since the Grundy number of the game of NIM with a heap of 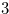 stones and a heap of
stones and a heap of 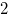 stones is
stones is 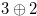 , the Grundy number of the chocolate bar in Figure 1.1 is
, the Grundy number of the chocolate bar in Figure 1.1 is 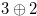 .
.
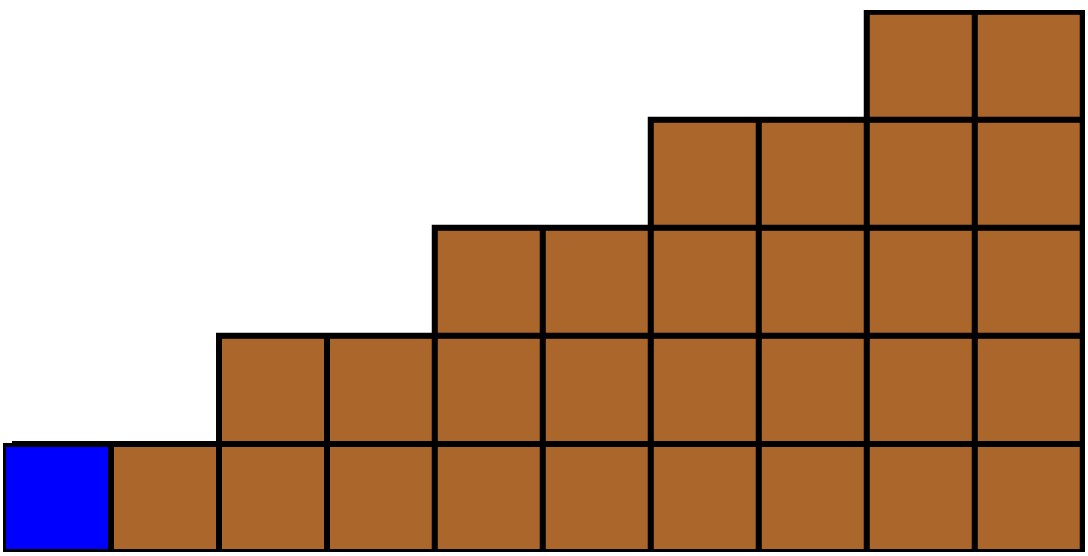
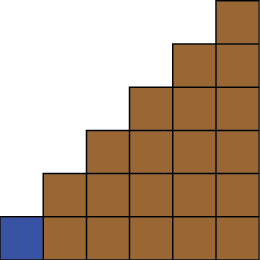
In this paper, we consider step chocolate bars as in Figures 1.2, 1.3, 1.4,1.5,1.6, 1.7 and etc. In these cases, a vertical break can reduce the number of horizontal breaks. We can still think of the game as being played with heaps but now a move may change more than one heap.
Next, we define coordinates {y,z} for each chocolate. Let 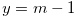 and
and 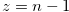 , where
, where 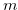 is is the largest width of the chocolate and
is is the largest width of the chocolate and 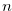 is the longest horizontal distance from the bitter part. (We use
is the longest horizontal distance from the bitter part. (We use 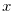 -coodinate later in this paper.)
-coodinate later in this paper.)
The 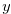 -coordinate and the
-coordinate and the  -cooridinate of each step chocolate bar in Figures 1.2, 1.3, 1.4, 1.5, 1.6, 1.7 are {3,13}, {4,9}, {2,9}, {5,5}, {3,11} and {2,14}. Here, the first number is the
-cooridinate of each step chocolate bar in Figures 1.2, 1.3, 1.4, 1.5, 1.6, 1.7 are {3,13}, {4,9}, {2,9}, {5,5}, {3,11} and {2,14}. Here, the first number is the 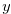 -coordinate and the second number is the
-coordinate and the second number is the  -coordinate of each chocolate. For an example, the
-coordinate of each chocolate. For an example, the 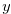 -coordinate and the
-coordinate and the  -cooridinate of the chocolate bar in Figure 1.2 are 3 and 13 respectively.
-cooridinate of the chocolate bar in Figure 1.2 are 3 and 13 respectively.
If we caluculate the Grundy numbers of chocolate bars in Figures 1.2, 1.3 and 1.4, we have 14=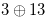 , 13=
, 13=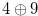 and 11=
and 11=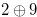 . (Here, we omit the calculation of Grundy numbers.)
. (Here, we omit the calculation of Grundy numbers.)
If we caluculate the Grundy numbers of chocolate bars in Figures 1.5, 1.6 and 1.7, then we have 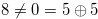 ,
, 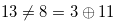 and
and 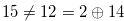 . (Here, we omit the calculation of Grundy numbers.) Now we know that the Grundy number of some step chocolates are
. (Here, we omit the calculation of Grundy numbers.) Now we know that the Grundy number of some step chocolates are 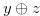 , where
, where 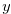 and
and  are coordinates of the chocolate, but the Grundy number of some step chocolates are not
are coordinates of the chocolate, but the Grundy number of some step chocolates are not 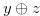 .
.
When the width of chocolate bar is proportional to the distance from the bitter square and the constant of proportionality is even, the authors have already proved that the Grundy number of this chocolate bar is 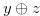 , where
, where 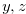 are the coordinates of the chocolate bar. This result was published in a mathematics journal (Integers, Volume 15, 2015). Chocolates in Figures 1.2, 1.3 and 1.4 are examples of this type of chocolates.
are the coordinates of the chocolate bar. This result was published in a mathematics journal (Integers, Volume 15, 2015). Chocolates in Figures 1.2, 1.3 and 1.4 are examples of this type of chocolates.
On the other hand, if the constant of proportionality is odd, the Grundy number of this chocolate bar is not 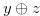 . Chocolates in Figures 1, 1 and 1 are examples of this type of chocolates.
. Chocolates in Figures 1, 1 and 1 are examples of this type of chocolates.
Therefore it is natural to look for a necessary and sufficient condition for chocolate bars to have the Grundy number that is equal to 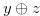 , where
, where 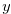 and
and  are coordinates of the chocolate.
are coordinates of the chocolate.
There are other types of chocolate bar games, and one of the most well known is CHOMP. CHOMP is a game with a rectangular chocolate bar. The players take turns, and they choose one block and eat it together with those that are below it and to its right. The top left block is bitter and the players cannot eat this block. Although many people have studied this game, the winning strategy is yet to be discovered. For an overview of research of CHOMP, see [3].

|

|
|
| {3,2} | {3,13} | {4,9} |
|
Grundy number is 1= 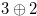 . .
|
Grundy number is 14= 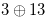 . .
|
Grundy number is 13=  . .
|

|
|

|
| {2,9} | {5,5} | {3,11} |
|
Grundy number is 11= 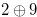 . .
|
Grundy number is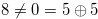 . .
|
Grundy number is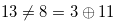 . .
|

|
||
| {2,14} | ||
Grundy number is 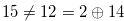 . .
|
Let 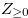 be the set of non-negative integers.
be the set of non-negative integers.
For completeness, we briefly review some necessary concepts in combinatorial game theory; see [4] or [5]for more details.
Definition 1.1. Let 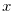 ,
, 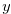 be non-negative integers, and write them in base 2, so that
be non-negative integers, and write them in base 2, so that 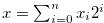 and
and 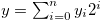 with
with 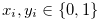 . We define the nim-sum
. We define the nim-sum 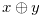 by
by
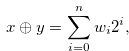 |
(1.1) |
where 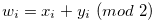 .
.
Since chocolate bar games are impartial games without draws there will only be two outcome classes.
Definition 1.2.
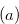
 -positions, from which the next player can force a win, as long as he plays correctly at every stage.
-positions, from which the next player can force a win, as long as he plays correctly at every stage.
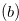
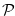 -positions, from which the previous player (the player who will play after the next player) can force a win, as long as he plays correctly at every stage.
-positions, from which the previous player (the player who will play after the next player) can force a win, as long as he plays correctly at every stage.
Definition 1.3. The disjunctive sum of two games, denoted 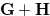 , is a super-game where a player may move either in
, is a super-game where a player may move either in 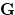 or in
or in  , but not both.
, but not both.
For any position 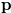 of a game
of a game 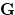 , there is a set of positions that can be reached by making precisely one move in
, there is a set of positions that can be reached by making precisely one move in 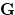 , which we will denote by move
, which we will denote by move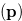 .
.
Remark 1.1. As to the examples of move, please see Example 2.3.
Definition 1.5. (i) The minimum excluded value (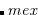 ) of a set,
) of a set, 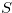 , of non-negative integers is the least non-negative integer which is not in S.
, of non-negative integers is the least non-negative integer which is not in S.
(ii) Each position 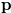 of a impartial game has an associated Grundy number, and we denoted it by
of a impartial game has an associated Grundy number, and we denoted it by 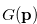 .
.
Grundy number is found recursively: 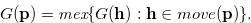
We present some lemmas for minimum excluded value 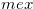 .
.
Lemma 1.1. Let 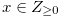 and
and 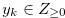 for
for 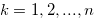 . Then Condition (i ) is true if and only if Condition (ii) is true.
. Then Condition (i ) is true if and only if Condition (ii) is true.
(i) 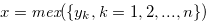 .
.
(ii) 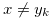 for any
for any 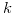 and for any
and for any 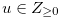 such that
such that 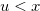 there exists
there exists 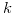 such that
such that 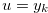 . This is direct from Definition 1.5 (the definition of
. This is direct from Definition 1.5 (the definition of 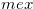 ).
).
Lemma 1.2. Let 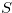 be a set and
be a set and 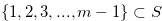 . Then
. Then 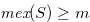 . This is direct from the definition of
. This is direct from the definition of 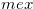 in Definition 1.5.
in Definition 1.5.
The power of the Sprague-Grundy theory for impartial games is contained in the next result.
Theorem 1.1. Let 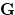 and
and  be impartial games, and let
be impartial games, and let 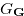 and
and 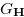 be Grundy numbers of
be Grundy numbers of 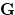 and
and  respectively. Then we have the following:
respectively. Then we have the following:
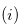 For any position
For any position 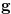 of
of 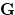 we have
we have 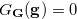 if and only if
if and only if 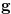 is a
is a 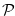 -position.
-position.
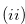 The Grundy number of a position
The Grundy number of a position 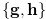 in the game
in the game 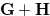 is
is 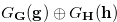 . For a proof of this theorem, see [4].
. For a proof of this theorem, see [4].