3.2 A Necessary Condition for a Chocolate Bar to have the Grundy Number 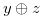
In Subsection 3.1, we proved that the Grundy number 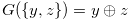 for
for 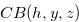 when the function
when the function 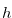 satisfies the condition
satisfies the condition 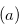 in Definition 3.2.
in Definition 3.2.
In this subsection, we prove that the condition 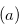 in Definition 3.2 is a necessary condition for
in Definition 3.2 is a necessary condition for 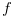 to have the Grundy number
to have the Grundy number 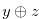 for the chocolate bar
for the chocolate bar 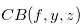 . Let
. Let 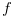 be a monotonically increasing function of
be a monotonically increasing function of 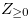 into
into 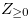 that satisfies the following condition
that satisfies the following condition 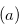 .
.
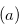 Suppose that
Suppose that 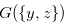 is the Grundy number of the chocolate bar
is the Grundy number of the chocolate bar 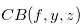 . Then,
. Then,
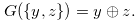 |
Throughout this subsection we assume that the function 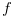 satisfies the condition
satisfies the condition 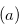 of Definition 3.4, and we prove that this function
of Definition 3.4, and we prove that this function 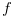 satisfies the condition
satisfies the condition 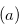 of Definition 3.2 using the following Lemma 3.9, Lemma 3.10 and Lemma 3.11.
of Definition 3.2 using the following Lemma 3.9, Lemma 3.10 and Lemma 3.11.
Lemma 3.9. Let 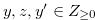 such that
such that  ,
, 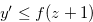 and
and 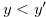 . Then,
. Then, 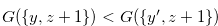 .
.
Proof. Since  , we have
, we have 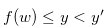 for
for  . Therefore,
. Therefore, 
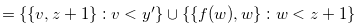
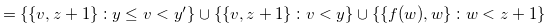
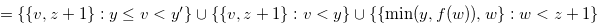
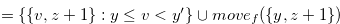 , where
, where  .
.
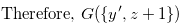 |
|||
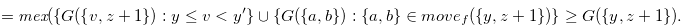 |
(3.44) |
Since 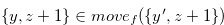 ,
, 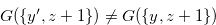 . Therefore, (3.44) implies
. Therefore, (3.44) implies 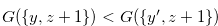 .
.
Lemma 3.10. For any 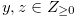 such that
such that  , we have
, we have 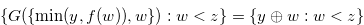 . Let
. Let 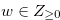 such that
such that 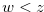 , and let
, and let
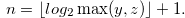 |
(3.45) |
Then, Equation (3.45) implies that 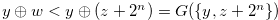 . By the definition of Grundy number, there exist
. By the definition of Grundy number, there exist 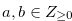 such that
such that 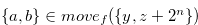 and
and 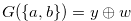 .
.
By the definition of 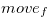 , we have the following Equation (3.46) or Equation (3.47).
, we have the following Equation (3.46) or Equation (3.47).
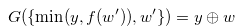 |
(3.46) |
for 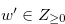 with
with 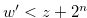 .
.
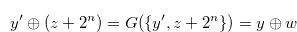 |
(3.47) |
for 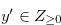 with
with 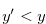 . Equation (3.47) contradicts Equation (3.45), and hence we have Equation (3.46).
. Equation (3.47) contradicts Equation (3.45), and hence we have Equation (3.46).
If
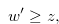 |
(3.48) |
then 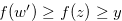 . Hence,
. Hence,
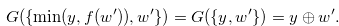 |
(3.49) |
By Equations (3.46) and (3.49), we have
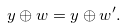 |
(3.50) |
Since 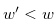 , Equation (3.50) leads to a contradiction. Therefore, the inequality in (3.48) is false, and we have
, Equation (3.50) leads to a contradiction. Therefore, the inequality in (3.48) is false, and we have 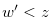 . Hence, Equation (3.46) implies that
. Hence, Equation (3.46) implies that 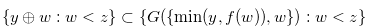 . The number of elements in
. The number of elements in 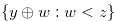 is the same as the number of elements in
is the same as the number of elements in 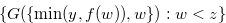 , and hence we have
, and hence we have 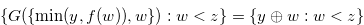 .
.
Lemma 3.11 Let
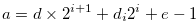 |
for 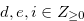 ,
, 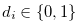 ,
, 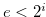 and
and 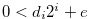 .
.
If 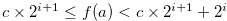 for
for 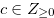 , then
, then 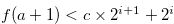 . Let
. Let
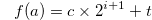 |
(3.51) |
for 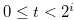 . We suppose that
. We suppose that
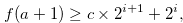 |
(3.52) |
and we show that this leads to a contradiction.
Case 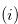 If
If 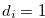 , then
, then
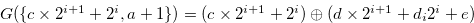
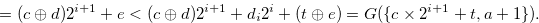 |
(3.53) |
By Equation (3.51), the inequality in (3.52) and Lemma 3.9, we have 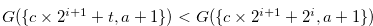 , which contradicts Equation (3.53).
, which contradicts Equation (3.53).
Case 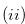 If
If  , then
, then 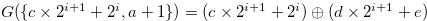
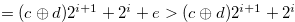 . Note that
. Note that 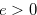 , since
, since 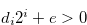 and
and  .
.
Therefore, by the definition of Grundy number we have
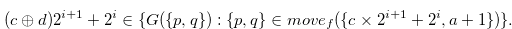 |
(3.54) |
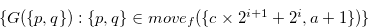
 |
|||
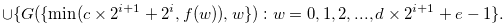 |
(3.55) |
Note that 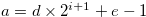 .
.
For 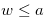 , we have
, we have 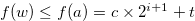 . Hence
. Hence
(3.55) 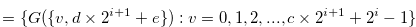 |
|||
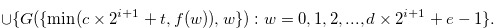 |
(3.56) |
Since 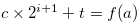
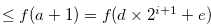 , Lemma 3.10 implies that
, Lemma 3.10 implies that 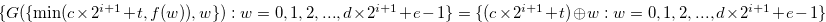 . Therefore, by Definition 3.4
. Therefore, by Definition 3.4
| (3.56) | 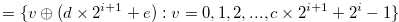 |
||
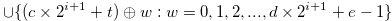 |
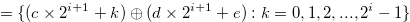 |
(3.57) | ||
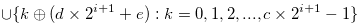 |
(3.58) | ||
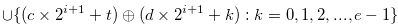 |
(3.59) | ||
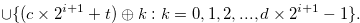 |
(3.60) |
Then we have the following statements 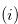 ,
, 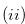 ,
, 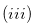 and
and 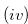 .
.
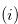 All the numbers in Set (3.57) are of the type
All the numbers in Set (3.57) are of the type 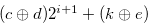 , and hence this set does not contains
, and hence this set does not contains 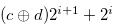 . Note that
. Note that 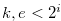 .
.
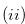 The coefficients of
The coefficients of 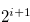 of the numbers in Set (3.58) are not
of the numbers in Set (3.58) are not 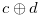 , and hence this set does not contains
, and hence this set does not contains 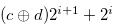 .
.
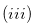 All the numbers in Set (3.59) are of the type
All the numbers in Set (3.59) are of the type 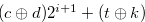 , and hence this set does not contains
, and hence this set does not contains 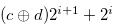 .
.
Note that  and
and 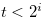 .
.
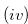 The coefficients of
The coefficients of 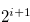 of the numbers in Set (3.60) are not
of the numbers in Set (3.60) are not 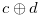 , and hence this set does not contains
, and hence this set does not contains 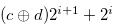 .
.
Statements 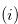 ,
, 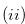 ,
, 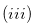 and
and 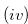 contradict Relation (3.54). Therefore we conclude that the inequality in (3.52) is false.
contradict Relation (3.54). Therefore we conclude that the inequality in (3.52) is false.
Theorem 3.3. Suppose that the function 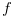 satisfies the condition
satisfies the condition 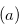 in Definition 3.4.
in Definition 3.4.
Then function 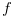 satisfies the condition
satisfies the condition 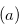 in Definition 3.2.
in Definition 3.2.
Proof. If 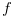 does not satisfy the condition in Definition 3.2, then there exist
does not satisfy the condition in Definition 3.2, then there exist 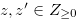 and a natural number
and a natural number 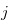 such that
such that 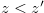 ,
,
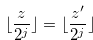 |
(3.61) |
and
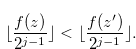 |
(3.62) |
By Equation (3.61), there exist 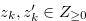 for
for  such that
such that 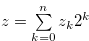 and
and 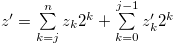 . By the inequality in (3.62), there exist
. By the inequality in (3.62), there exist 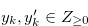 for
for  and a natural number
and a natural number 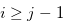 such that
such that 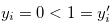 ,
,
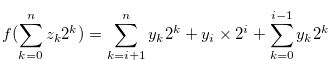 |
(3.63) |
and
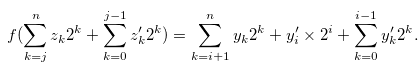 |
(3.64) |
Let 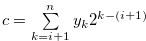 . Then
. Then 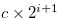
 . Hence Equations (3.63) and (3.64) imply that
. Hence Equations (3.63) and (3.64) imply that
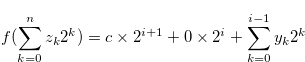 |
(3.65) |
and
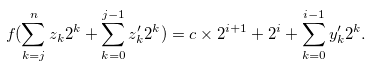 |
(3.66) |
Let
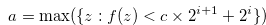 |
(3.67) |
and
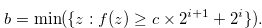 |
(3.68) |
Then, 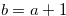 follows directly from (3.67) and (3.68). Let
follows directly from (3.67) and (3.68). Let 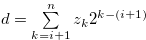 . Then,
. Then, 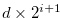
 . By (3.65),
. By (3.65),
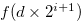
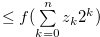
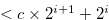 , and hence Equation (3.67) implies
, and hence Equation (3.67) implies
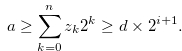 |
(3.69) |
By 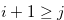 , we have
, we have 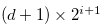
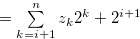
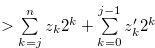 .
.
Hence Equations (3.68), (3.66) and the inequality in (3.69) implies that 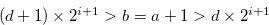 . Therefore, there exist
. Therefore, there exist 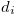 and
and 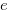 such that
such that 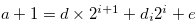 ,
, 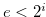 and
and  .
.
By Equation (3.65) and the inequality in (3.69), we have
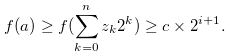 |
(3.70) |
Equation (3,67) implies
 |
(3.71) |
and
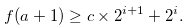 |
(3.72) |
Inequalities (3.70), (3.71) and (3.72) contradict the result of Lemma 3.11, and hence that 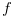 satisfies the condition in Definition 3.1. By Theorem 3.3, the condition
satisfies the condition in Definition 3.1. By Theorem 3.3, the condition 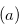 in Definition 3.1 is a necessary condition for
in Definition 3.1 is a necessary condition for 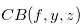 to have the Grundy number
to have the Grundy number 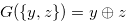 .
.
 whose Grundy number is
whose Grundy number is 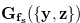
 for a fixed natural number s
for a fixed natural number s