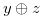3.1 A Sufficient Condition for a Chocolate Bar 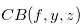 to have the Grundy Number
to have the Grundy Number 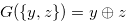
In this subsection we study a sufficient condition for a chocolate bar 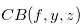 to have a Grundy number
to have a Grundy number 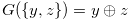 .
.
In our proofs, it will be useful to have the disjunctive sum of a chocolate bar 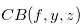 to the right of the bitter square and a single strip of chocolate bar to the left, as in Figures 3.1, 3.2, 3.3, 3.4, 3.5 and 3.6. We will denote such a position by
to the right of the bitter square and a single strip of chocolate bar to the left, as in Figures 3.1, 3.2, 3.3, 3.4, 3.5 and 3.6. We will denote such a position by 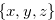 , where
, where 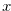 is the length of the single strip of chocolate bar and
is the length of the single strip of chocolate bar and 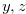 are coordinates of
are coordinates of 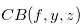 . Figures 3.4, 3.5 and 3.6 give some examples of the coordinate system. For the disjunctive sum of the chocolate bar game with
. Figures 3.4, 3.5 and 3.6 give some examples of the coordinate system. For the disjunctive sum of the chocolate bar game with 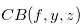 to the right of the bitter square and a single strip of chocolate bar to the left, we will show that the
to the right of the bitter square and a single strip of chocolate bar to the left, we will show that the  -positions are when
-positions are when 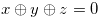 , so that the Grundy number of the chocolate bar
, so that the Grundy number of the chocolate bar 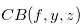 is
is 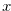
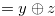 .
.
Example 3.1. Examples of coordinates of chocolate bar games.

Figure 3.1.
{4,7,12}
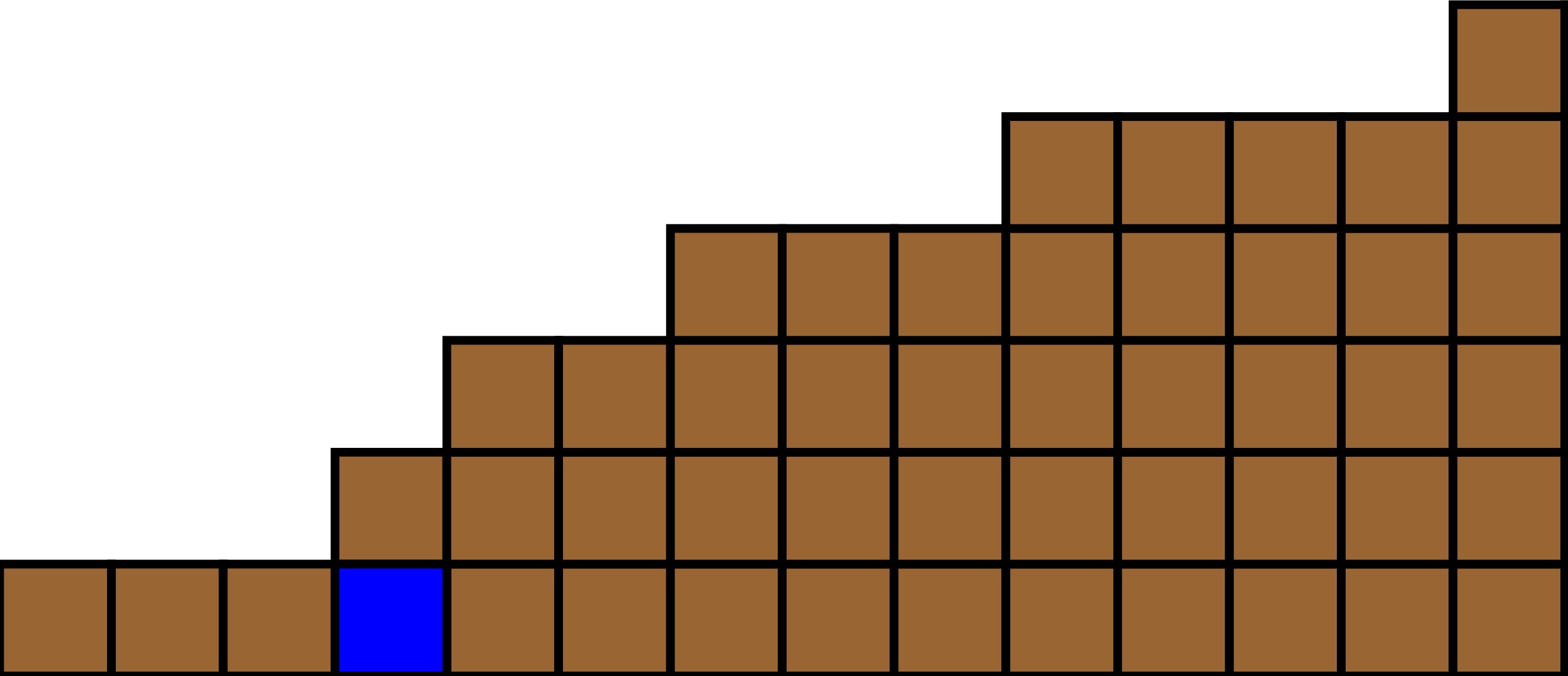
Figure 3.2.
{3,5,10}
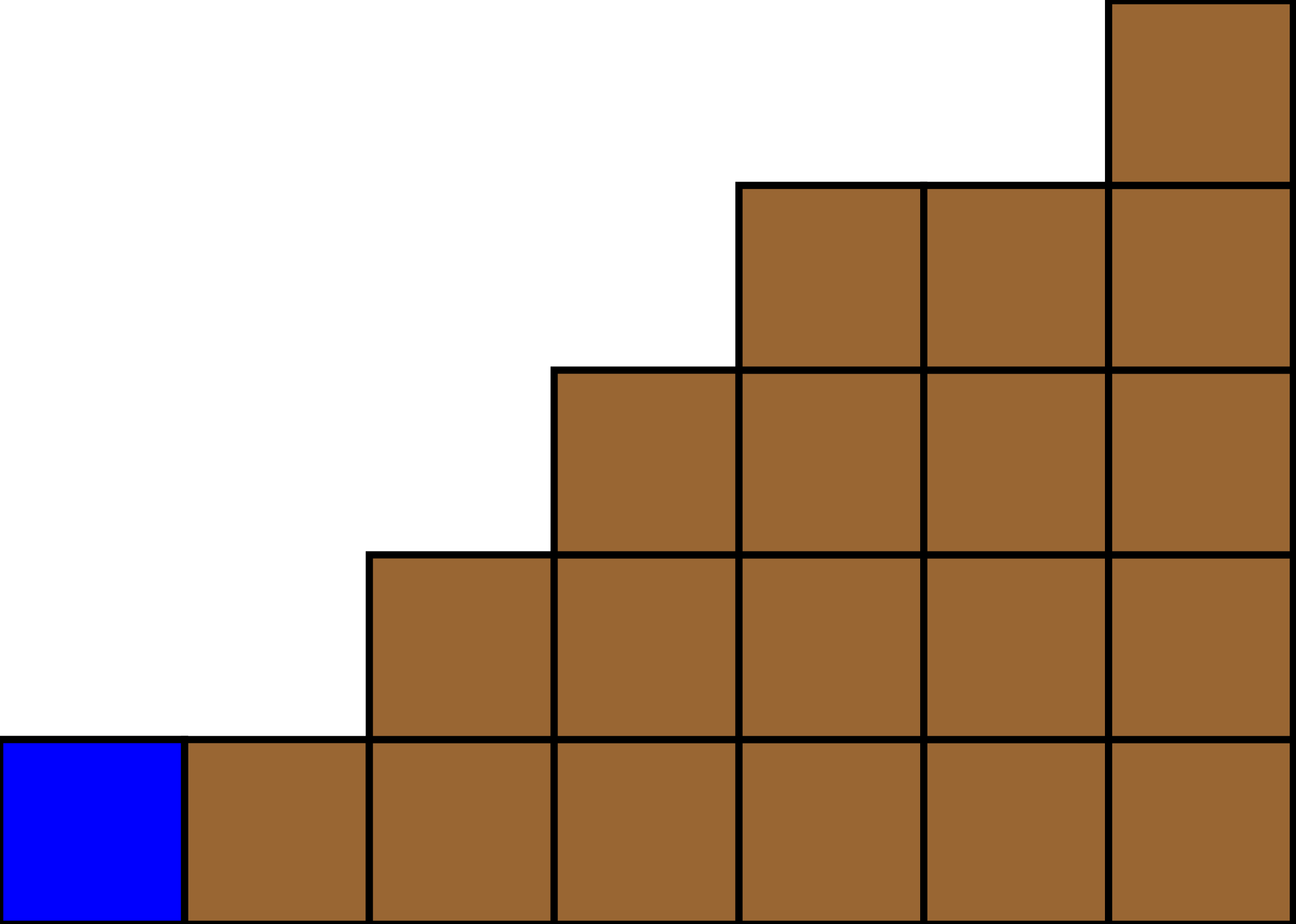
Figure 3.3.
{0,4,6}
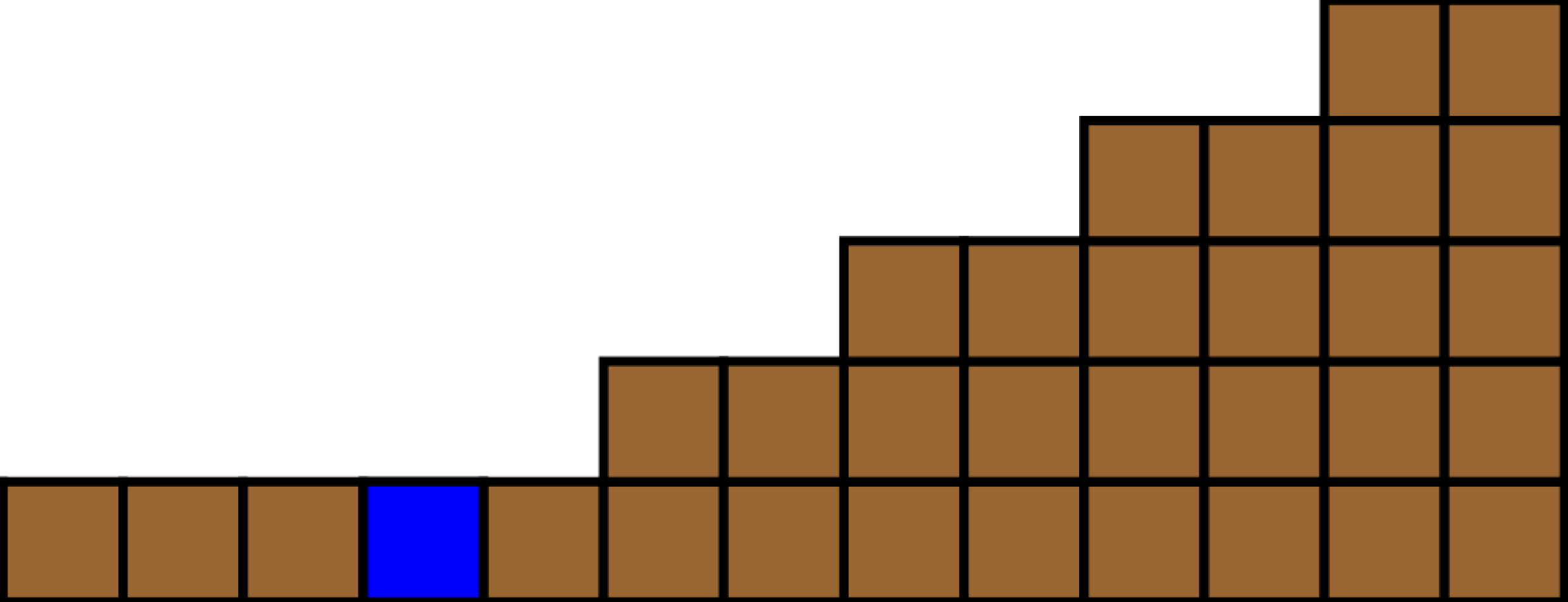
Figure 3.4.

Figure 3.5.


Figure 3.6.
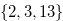
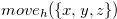 is the set that contains all the positions that can be reached from the position
is the set that contains all the positions that can be reached from the position 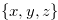 in one step (directly).
in one step (directly).
Definition 3.1. For 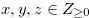 , we define
, we define 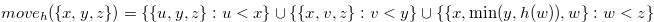 , where
, where 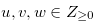 .
.
The following condition 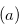 in Definition 3.2 is a sufficient condition for a chocolate bar
in Definition 3.2 is a sufficient condition for a chocolate bar 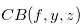 to have a Grundy number
to have a Grundy number 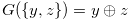 .
.
Definition 3.2. Let 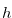 be a function of
be a function of 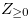 into
into 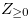 that satisfies the conditions of Definition 2.1. and the following condition
that satisfies the conditions of Definition 2.1. and the following condition 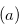 .
.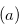 Suppose that
Suppose that
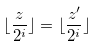 |
(3.1) |
for some 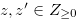 and some natural number
and some natural number 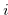 . Then we have
. Then we have
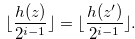 |
(3.2) |
Remark 3.1. The condition 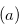 of Definition 3.2 is equivalent to the following condition
of Definition 3.2 is equivalent to the following condition 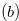 .
.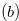 Suppose that
Suppose that 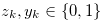 for
for 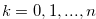 and
and
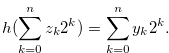 |
Let 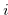 be a natural number. Then for any
be a natural number. Then for any 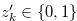 for
for 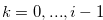 there exist
there exist 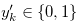 for
for 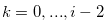 such that
such that
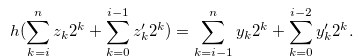 |
The condition  of Definition 3.2 is very abstract, so we present some examples of functions that satisfy condition
of Definition 3.2 is very abstract, so we present some examples of functions that satisfy condition  of Definition 3.2 in Lemma 3.1 and Lemma3.2.
of Definition 3.2 in Lemma 3.1 and Lemma3.2.
Lemma 3.1. Let 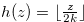 for some natural number
for some natural number 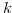 . Then
. Then  satisfies the condition of Definition 3.2. We prove the contraposition of the condition of Definition 3.2. We suppose that Equation (3.2) is false. Then there exist
satisfies the condition of Definition 3.2. We prove the contraposition of the condition of Definition 3.2. We suppose that Equation (3.2) is false. Then there exist 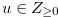 and a natural number
and a natural number 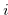 such that
such that
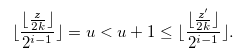 |
(3.3) |
We prove that Equation (3.1) is false. From the inequality in (3.3), we have
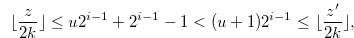 |
and hence
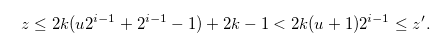 |
(3.4) |
From the inequality in (3.4), we have
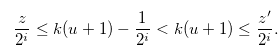 |
Therefore we have
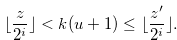 |
This shows that Equation (3.1) is false. Therefore, we have completed the proof of this lemma.
Lemma 3.2. Let 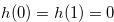 and
and  for
for 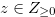 such that
such that  . Then
. Then  satisfies the condition of Definition 3.2. We prove the contraposition of the condition of Definition 3.2. Suppose that Equation (3.2) is false. Then for a natural number
satisfies the condition of Definition 3.2. We prove the contraposition of the condition of Definition 3.2. Suppose that Equation (3.2) is false. Then for a natural number 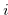
 |
(3.5) |
We prove that Equation (3.1) is false. Let 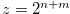 and
and 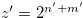 such that
such that 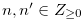 and
and 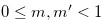 . Then by the inequality in (3.5), we have
. Then by the inequality in (3.5), we have
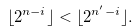 |
(3.6) |
By the inequality in (3.6), we have
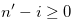
|
(3.7) | ||
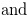 |
|||
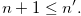 |
(3.8) |
By the inequalities in (3,7) and (3.8), we have
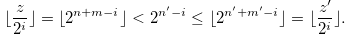 |
This shows that Equation (3.1) is false. Therefore we have completed the proof.
In the remainder of this subsection we assume that 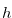 is the function that satisfies the condition
is the function that satisfies the condition 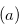 in Definition 3.2. Our aim is to show that the disjunctive sum of the chocolate bar game with
in Definition 3.2. Our aim is to show that the disjunctive sum of the chocolate bar game with 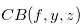 to the right of the bitter square and a single strip of chocolate bar to the left have
to the right of the bitter square and a single strip of chocolate bar to the left have 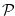 -positions when
-positions when 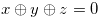 , so that the Grundy number of the chocolate bar
, so that the Grundy number of the chocolate bar 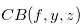 is
is 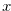
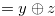 .
.
We need Lemma3.6and Lemma3.7 for this aim. Lemma 3.6 implies that from a position 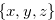 of the disjunctive sum such that
of the disjunctive sum such that 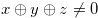 you always have a option that leads to a position for which the nim-sum of the coordinates is
you always have a option that leads to a position for which the nim-sum of the coordinates is 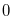 . Lemma 3.7 implies that from a position
. Lemma 3.7 implies that from a position 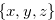 of the disjunctive sum such that
of the disjunctive sum such that 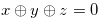 any option leads to a position for which the nim-sum of the coordinates is not
any option leads to a position for which the nim-sum of the coordinates is not 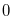 .
.
To prove Lemma 3.6 and Lemma 3.7 we need some properties of the function 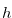 that satisfies the condition
that satisfies the condition 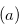 in Definition 3.2. These properties are proved in Lemma 3.3, Lemma 3.4 and Lemma 3.5.
in Definition 3.2. These properties are proved in Lemma 3.3, Lemma 3.4 and Lemma 3.5.
Lemma 3.3. Suppose that
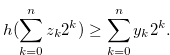 |
(3.9) |
Then, for any natural number 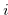 ,
,
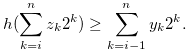 |
Proof. Let 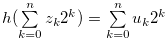 for
for 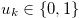 . Then, by the inequality in (3.9),
. Then, by the inequality in (3.9),
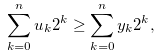 |
and hence
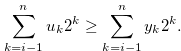 |
(3.10) |
Let  for
for 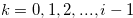 . By the inequality in (3.10), Definition 3.2 and Remark 3.1, there exist
. By the inequality in (3.10), Definition 3.2 and Remark 3.1, there exist 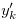 for
for 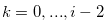 such that
such that
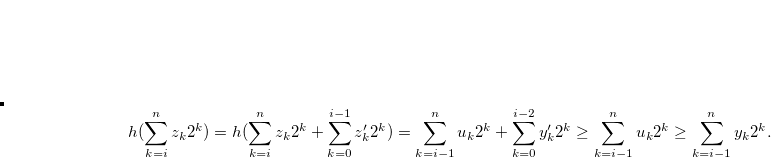 |
Lemma 3.4.
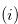 Suppose that for some natural number
Suppose that for some natural number 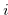
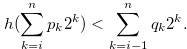 |
(3.11) |
Then
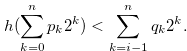 |
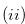 Suppose that
Suppose that
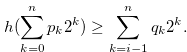 |
Then
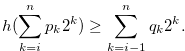 |
We prove 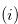 . Let
. Let 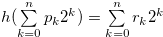 for
for 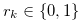 . Then, by Remark 3.1, there exist
. Then, by Remark 3.1, there exist 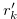 for
for 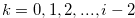 such that
such that 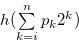
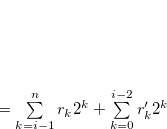 . Then, by the inequality in (3.11), we have
. Then, by the inequality in (3.11), we have
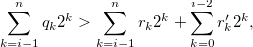 |
and hence we have the inequality in (3.12) or Relation (3.13).
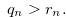 |
(3.12) |
There exists 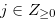 such that
such that
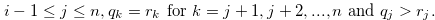 |
(3.13) |
Then, by the inequality in (3.12) or Relation (3.13),
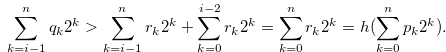 |
We prove 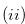 . This is the contraposition of the proposition in
. This is the contraposition of the proposition in 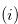 of this lemma.
of this lemma.
Lemma 3.5. Suppose that
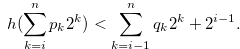 |
(3.14) |
Then
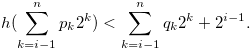 |
Proof. Let 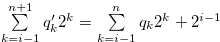 and
and  . Then, by the inequality in (3.14), we have
. Then, by the inequality in (3.14), we have 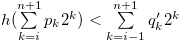 , and statement
, and statement 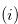 of Lemma 3,4 implies
of Lemma 3,4 implies 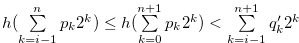
 . Therefore we have completed the proof of this lemma.
. Therefore we have completed the proof of this lemma.
If the nim-sum of the cooridinates of a position is not 0, then by Definition 3.1and the following Lemma 3.6, there is always an option that leads to a position whose nim-sum is 0.
Lemma 3.6. Suppose that 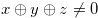 and
and
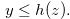 |
(3.15) |
Then at least one of the following statements is true.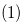
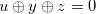 for some
for some 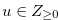 such that
such that 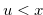 .
.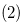
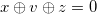 for some
for some 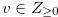 such that
such that 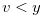 .
.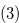
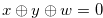 for some
for some 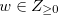 such that
such that 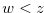 and
and 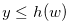 .
.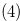
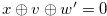 for some
for some 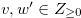 such that
such that 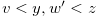 and
and 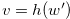 .
.
Proof. Let 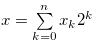 ,
, 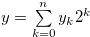 and
and  . If
. If 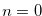 , then this lemma is obvious. We assume that
, then this lemma is obvious. We assume that 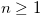 . Suppose that there exists a non-negative integer
. Suppose that there exists a non-negative integer 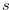 such that
such that 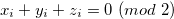 for
for  and
and
 |
(3.16) |
Case 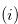 Suppose that
Suppose that 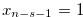 . Then, we define
. Then, we define  by
by 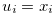 for
for 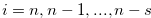 ,
, 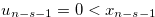 and
and 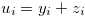
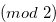 for
for 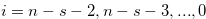 . Then we have
. Then we have 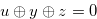 and
and 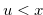 . Therefore, we have statement
. Therefore, we have statement 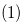 of this lemma.
of this lemma.
Case 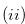 Suppose that
Suppose that 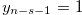 . Then, by the method that is similar to the one used in
. Then, by the method that is similar to the one used in 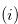 , we prove that
, we prove that 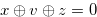 for some
for some 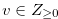 such that
such that 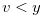 . Therefore we have statement
. Therefore we have statement 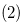 of this lemma.
of this lemma.
Case 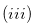 We suppose that
We suppose that
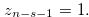 |
(3.17) |
For  , let
, let
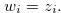 |
(3.18) |
Let 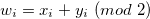 for
for 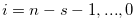 . By the inequality in (3.16) and Equation (3.17), we have
. By the inequality in (3.16) and Equation (3.17), we have 

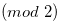 , and hence
, and hence
 |
(3.19) |
Subcase 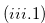 If
If 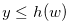 , then we have statement
, then we have statement 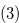 of this lemma.
of this lemma.
Subcase 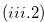 Next we suppose that
Next we suppose that
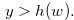 |
(3.20) |
By the inequality in (3.15), we have 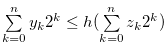 , and hence by Lemma 3.3 and (3.18)
, and hence by Lemma 3.3 and (3.18)
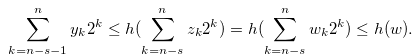 |
(3.21) |
By the inequalities in (3.21) and (3.20), there exists a natural number 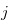 such that
such that
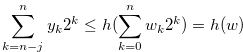 |
(3.22) | ||
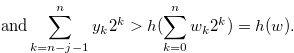 |
(3.23) |
By the inequalities in (3.21) and (3.23),
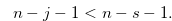 |
(3.24) |
By the inequality in (3.22) and 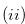 of Lemma 3.4,
of Lemma 3.4,
 |
(3.25) |
By the inequality in (3.23),
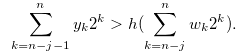 |
(3.26) |
By the inequalities in (3.25) and (3.26), we have
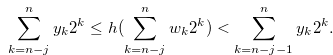 |
(3.27) |
We construct 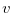 and
and 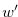 by assigning values to
by assigning values to 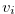 and
and 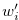 for
for 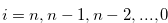 . First, for
. First, for 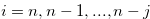 , let
, let
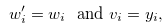 |
(3.28) |
and let
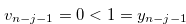 |
(3.29) |
and
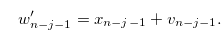 |
Since 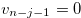 and
and 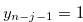 , by the inequality in (3.27)
, by the inequality in (3.27)
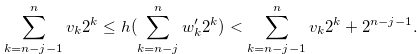 |
(3.30) |
By the inequality in (3.30) and Lemma 3.5, we have
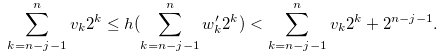 |
(3.31) |
Next we prove the inequality in (3.32) for any 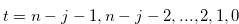 recursively.
recursively.
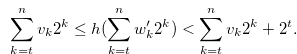 |
(3.32) |
By the inequality in (3.31), we have the inequality in (3.32) for 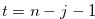 . We suppose the inequality in (3.32) for some natural number
. We suppose the inequality in (3.32) for some natural number 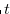 such that
such that 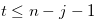 . Then we have the inequality in (3.33) or the inequality in (3.36). Our aim is to prove (3.35) and (3.38) by using these inequalities.
. Then we have the inequality in (3.33) or the inequality in (3.36). Our aim is to prove (3.35) and (3.38) by using these inequalities.
If
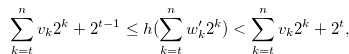 |
(3.33) |
then let 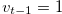 and
and 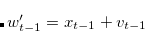
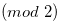 . Since
. Since 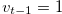 , by the inequality in (3.33) we have
, by the inequality in (3.33) we have
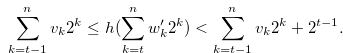 |
(3.34) |
Note that 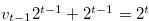 . By Lemma 3.5 and the inequality in (3.34),
. By Lemma 3.5 and the inequality in (3.34),
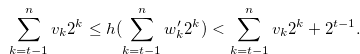 |
(3.35) |
If
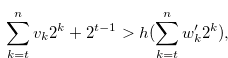 |
(3.36) |
then let 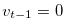 and
and 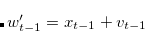
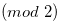 .
.
Since 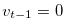 , the inequalities in (3.36) and (3.32) give
, the inequalities in (3.36) and (3.32) give
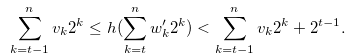 |
(3.37) |
Then, by the inequality in (3.37) and Lemma 3.5, we have
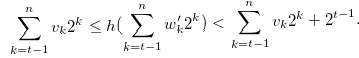 |
(3.38) |
In this way we get the inequality in (3.35) or the inequality in (3.38) by the inequality in (3.32). Note that the inequality in (3.35) and the inequality in (3.38) are the same inequality. By continuing this process we have
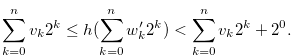 |
Therefore, we have 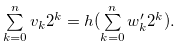 By iequalities (3.19), (3.24), (3.29) and Equation (3.28), we have
By iequalities (3.19), (3.24), (3.29) and Equation (3.28), we have 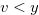 and
and 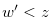 . Therefore, we have statement
. Therefore, we have statement 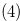 of this lemma. If the nim-sum of the cooridinates of a position is 0, then by Definition 3.1 and the following Lemma 3.7, any option from this position leads to a position whose nim-sum is not 0.
of this lemma. If the nim-sum of the cooridinates of a position is 0, then by Definition 3.1 and the following Lemma 3.7, any option from this position leads to a position whose nim-sum is not 0.
Lemma 3.7. If 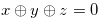 and
and 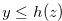 , then the following hold:
, then the following hold: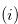
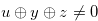 for any
for any 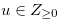 such that
such that 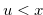 .
.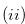
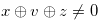 for any
for any 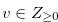 such that
such that 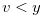 .
.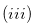
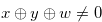 for any
for any 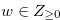 such that
such that 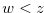 .
.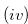
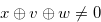 for any
for any  such that
such that  and
and 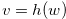 . Statements
. Statements 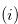 ,
,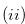 and
and 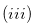 of this lemma follow directly from Definition 1 (the definition of nim-sum).
of this lemma follow directly from Definition 1 (the definition of nim-sum).
We now prove statement 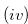 . We suppose that
. We suppose that 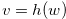 for some
for some 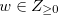 such that
such that  . We also suppose that
. We also suppose that
 |
(3.39) |
By 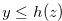 , we have
, we have 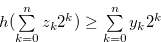 . Hence, by Lemma 3.3, we have
. Hence, by Lemma 3.3, we have
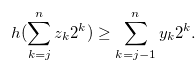 |
(3.40) |
Since 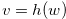 and
and 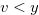 , Relation (3.39) gives
, Relation (3.39) gives
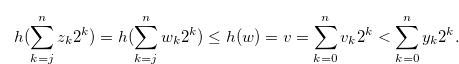 |
(3.41) |
By the inequalities in (3.40) and (3.41), we have
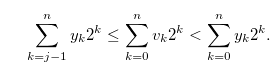 |
Hence, for 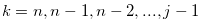 ,
,
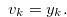 |
(3.42) |
Since 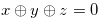 , we have
, we have
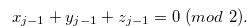 |
(3.43) |
By Relation (3.39), Equation (3.42) and Equation (3.43), we have 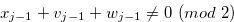 , and hence
, and hence  .
.
Let 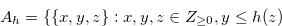 and
and 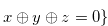 and
and 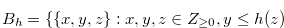 and
and 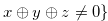 .
.
Let 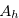 and
and 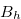 be the sets defined in Definition 3.3. Then the following hold:
be the sets defined in Definition 3.3. Then the following hold: If we start with a position in
If we start with a position in 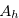 , then any option (move) leads to a position in
, then any option (move) leads to a position in 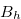 .
.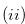 If we start with a position in
If we start with a position in 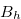 , then there is at least one option (move) that leads to a position in
, then there is at least one option (move) that leads to a position in 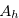 .
.
Since 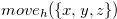 that is defined in Definition 3.1 contains all the positions that can be reached from the position
that is defined in Definition 3.1 contains all the positions that can be reached from the position 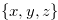 in one step, we have statements
in one step, we have statements 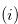 and
and 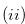 by Lemma 3.7 and Lemma 3.6 respectively.
by Lemma 3.7 and Lemma 3.6 respectively.
Theorem 3.1. Let 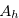 and
and 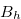 be the sets defined in Definition 3.3.
be the sets defined in Definition 3.3. 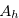 is the set of
is the set of  -positions and
-positions and 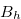 is the set of
is the set of  -positions of the disjunctive sum of the chocolate bar game with
-positions of the disjunctive sum of the chocolate bar game with 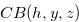 to the right of the bitter square and a single strip of chocolate bar to the left. If we start the game from a position
to the right of the bitter square and a single strip of chocolate bar to the left. If we start the game from a position 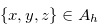 , then Lemma 3.8 indicates that any option we take leads to a position
, then Lemma 3.8 indicates that any option we take leads to a position 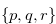 in
in 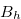 . From this position
. From this position 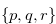 , Lemma 3.8 implies that our opponent can choose a proper option that leads to a position in
, Lemma 3.8 implies that our opponent can choose a proper option that leads to a position in 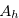 . Note that any option reduces some of the numbers in the coordinates. In this way, our opponent can always reach a position in
. Note that any option reduces some of the numbers in the coordinates. In this way, our opponent can always reach a position in 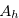 , and will finally win by reaching
, and will finally win by reaching 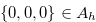 . Note that position
. Note that position 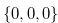 represent the bitter square itself, and we cannot eat this part. Therefore
represent the bitter square itself, and we cannot eat this part. Therefore 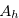 is the set of
is the set of  -positions.
-positions.
If we start the game from a position 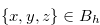 , then Lemma 3.8 means that we can choose a proper option that leads to a position
, then Lemma 3.8 means that we can choose a proper option that leads to a position 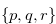 in
in 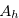 . From
. From 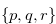 , Lemma 3.8 implies that any option taken by our opponent leads to a position in
, Lemma 3.8 implies that any option taken by our opponent leads to a position in 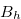 . In this way we win the game by reaching
. In this way we win the game by reaching 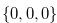 . Note that our opponent cannot eat the bitter part. Therefore
. Note that our opponent cannot eat the bitter part. Therefore 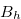 is the set of
is the set of  -position
-position
Theorem 3.2 Let 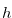 be the function that satisfies the condition
be the function that satisfies the condition 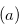 in Definition 3.2. Then the Grundy number of
in Definition 3.2. Then the Grundy number of 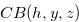 is
is 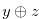 .
.
Proof. By Theorem 3.1, a position 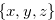 of the sum of the chocolate bars is a
of the sum of the chocolate bars is a 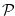 -position when
-position when 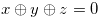 . Therefore, Theorem 1.1 implies that the Grundy number of the chocolate bar to the right is
. Therefore, Theorem 1.1 implies that the Grundy number of the chocolate bar to the right is 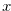
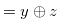 .
.
By Theorem 3,2, the condition of Definition 3.2 is a sufficient condition for the chocolate bar 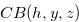 to have the Grundy number
to have the Grundy number 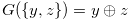 . Lemma 3.1, Lemma 3.2 and Theorem 3.2 imply that chocolate bar games in Figure 2.1, Figure 2.2, Figure 2.3 and Figure 2.4 have the Grundy number
. Lemma 3.1, Lemma 3.2 and Theorem 3.2 imply that chocolate bar games in Figure 2.1, Figure 2.2, Figure 2.3 and Figure 2.4 have the Grundy number 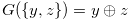 .
.
In the next subsection we prove that the condition of Definition 3.2 is a necessary condition for the chocolate bar 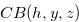 to have the Grundy number
to have the Grundy number 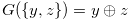 .
.