4.2 A Necessary Condition for a Chocolate Bar to have the Grundy Number 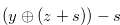$(y \oplus (z+s))-s$.

In this subsection, we study a necessary condition for a chocolate bar to have the Grundy number 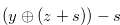$(y \oplus (z+s))-s$.

 

Definition 4.2. Let 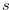$s$ be a fixed natural number and 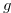$g$ be a function that satisfies the following three conditions:
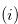
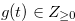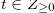$(i)$ $g(t)\in Z_{\geq 0}$ for $t \in Z_{\geq 0}$.
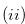
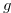$(ii)$ $g$ is monotonically increasing.
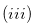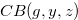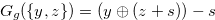$(iii)$ The Grundy number of $CB(g,y,z)$ is $G_ g(\{ y,z\} )= (y \oplus (z+s))-s$.

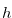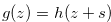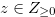We are going to show that there exists a function $h$ such that $g(z) = h(z+s)$ for any $z \in Z_{\geq 0}$,

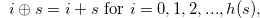  \begin{equation} \nonumber i \oplus s = i + s \text { for } i = 0,1,2,...,h(s), \end{equation}    

and the Grundy number of 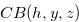$CB(h,y,z)$ is $G_ h(\{ y,z\} )= (y \oplus z)$.

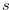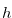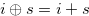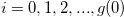Lemma 4.6. Let $s$ be a natural number and $h$ a function such that the conditions of Definition 4.2 are satisfied. Then we have $i \oplus s = i + s$ for $i=0,1,2,...,g(0)$.

Proof. First, we prove that

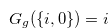  \begin{equation} \label{conditionGrundyg} G_ g(\{ i,0\} )=i \end{equation}   (4.20)

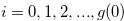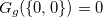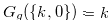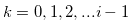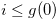for $i = 0,1,2,...,g(0)$ by mathematical induction. By the definition of Grundy number, $G_ g(\{ 0,0\} )=0$. We suppose that $G_ g(\{ k,0\} )=k$ for $k = 0,1,2,...i-1$ and $i \leq g(0)$. By the definition of Grundy number,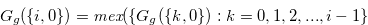 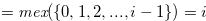$G_ g(\{ i,0\} )=\textit{mex}(\{ G_ g(\{ k,0\} ):k=0,1,2,...,i-1\} $ $=\textit{mex}(\{ 0,1,2,...,i-1\} )=i$. By the conditions of Definition 4.2, we have 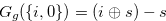$G_ g(\{ i,0\} )= (i \oplus s)-s$, and hence Equation (4.20) implies 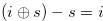$(i \oplus s)-s = i$. Therefore, we have completed the proof.

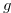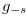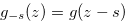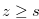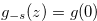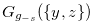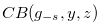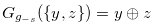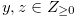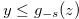Theorem 4.2. Let $s$ be a natural number and $g$ a function such that the conditions of Definition 4.2 are satisfied. We define a function $g_{-s}$ by $g_{-s}(z)=g(z-s)$ for $z \geq s$ and $g_{-s}(z)=g(0)$ for $0 \leq z < s$. Let $G_{g_{-s}}(\{ y,z\} )$ be the Grundy number of $CB(g_{-s},y,z)$. Then $G_{g_{-s}}(\{ y,z\} )= y \oplus z$ for any $y,z \in Z_{\geq 0}$ such that $y \leq g_{-s}(z)$.

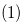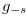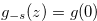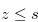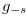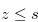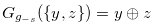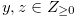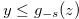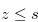Proof. Case $(1)$ By the definition of $g_{-s}$, we have $g_{-s}(z)=g(0)$ for $z \leq s$, and hence the function $g_{-s}$ satisfies the condition of Definition 3.2 for $z \leq s$. Therefore $G_{g_{-s}}(\{ y,z\} )= y \oplus z$ for any $y,z \in Z_{\geq 0}$ such that $y \leq g_{-s}(z)$ and $z \leq s$.
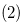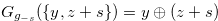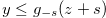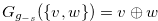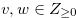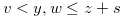Case $(2)$ Next we prove that $G_{g_{-s}}(\{ y,z+s\} )= y \oplus (z+s)$ for $y \leq g_{-s}(z+s)$. We prove by mathematical induction, and we assume that $G_{g_{-s}}(\{ v,w\} )= v \oplus w$ for $v,w \in Z_{\geq 0}$ such that $v \leq y, w< z+s$ or $v < y, w \leq z+s$. By Lemma 4.2 and Lemma 4.6, we have Relation (4.21).

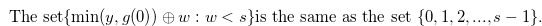  \begin{equation} \label{equal0s} \text {The set} \{ \min (y,g(0)) \oplus w:w < s\} \text {is the same as the set } \{ 0,1,2,...,s-1\} . \end{equation}   (4.21)

By Definition 4.2,

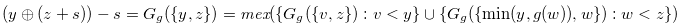  $\displaystyle (y \oplus (z+s))-s=G_ g(\{ y,z\} )=\textit{mex}(\{ G_ g(\{ v,z\} ):v<y\} \cup \{ G_ g(\{ \min (y,g(w)),w\} ):w < z\} )\nonumber $    
  $\displaystyle =\textit{mex}(\{ (v \oplus (z+s))-s:v<y\} \cup \{ (\min (y,g_{-s}(w+s)) \oplus (w+s))-s :s \leq w+s < z+s\} ).\label{gstoordinaryg} $   (4.22)
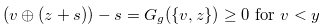  $\displaystyle (v \oplus (z+s))-s = G_ g(\{ v,z\} ) \geq 0 \text { for } v<y \hspace{3cm}\nonumber $    
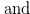  $\displaystyle \text { and }\hspace{8cm} \nonumber $    
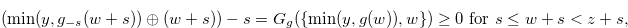  $\displaystyle (\min (y,g_{-s}(w+s)) \oplus (w+s))-s = G_ g(\{ \min (y,g(w)),w\} ) \geq 0 \text { for } s \leq w+s < z+s, \nonumber $    

and hence we have

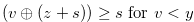  $\displaystyle (v \oplus (z+s)) \geq s \text { for } v<y \hspace{3cm} \label{eqgrundy1} $   (4.23)
  $\displaystyle \text { and }\hspace{5.2cm} \nonumber $    
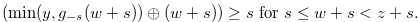  $\displaystyle (\min (y,g_{-s}(w+s)) \oplus (w+s)) \geq s \text { for } s \leq w+s < z+s. \label{eqgrundy2} $   (4.24)
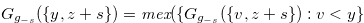  $\displaystyle G_{g_{-s}}(\{ y,z+s\} ) =\textit{mex}(\{ G_{g_{-s}}(\{ v,z+s\} ):v<y\} \hspace{2cm} \nonumber $    
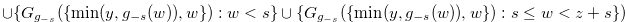  $\displaystyle \cup \{ G_{g_{-s}}(\{ \min (y,g_{-s}(w)),w\} ):w < s\} \cup \{ G_{g_{-s}}(\{ \min (y,g_{-s}(w)),w\} ):s \leq w < z+s\} )\nonumber $    
  \begin{equation} =\textit{mex}(\{ v \oplus (z+s):v<y\} \cup \{ \min (y,g_{-s}(w)) \oplus w:w < s\} \cup \{ \min (y,g_{-s}(w)) \oplus w :s \leq w < z+s\} ).\label{fromgstog1} \end{equation}   (4.25)

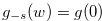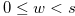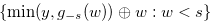
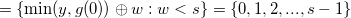Since $g_{-s}(w)=g(0)$ for $0 \leq w < s$, Relation (4.21) implies $\{ \min (y,g_{-s}(w)) \oplus w:w < s\} $ $= \{ \min (y,g(0)) \oplus w:w < s\} =\{ 0,1,2,...,s-1\} $.

Hence, Equation (4.22), the inequality in (4.23), the inequality in (4.24), Equation (4.25) and Lemma4.3 imply 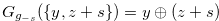$G_{g_{-s}}(\{ y,z+s\} )=y \oplus (z+s)$.

Theorem 4.1 and Theorem 4.2 prove the following proposition $(i)$ and $(ii)$ respectively.
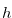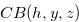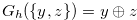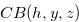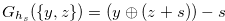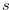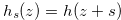$(i)$ Let $h$ be a function such that the Grundy number of the chocolate bar $CB(h,y,z)$ is $G_ h(\{ y,z\} ) = y \oplus z$. Then the Grundy number of the chocolate bar $CB(h,y,z)$ is $G_{h_ s}(\{ y,z\} ) = (y \oplus (z+s))-s$, where $s$ satisfies the condition (4.18) and $h_ s(z)=h(z+s)$.
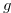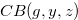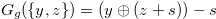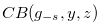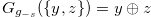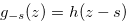$(ii)$ Let $g$ be a function such that the Grundy number of the chocolate bar $CB(g,y,z)$ is $G_ g(\{ y,z\} ) = (y \oplus (z+s))-s$. Then the Grundy number of the chocolate bar $CB(g_{-s},y,z)$ is $G_{g_{-s}}(\{ y,z\} ) = y \oplus z$, where $g_{-s}(z)=h(z-s)$. Note that $g=(g_{-s})_ s$.
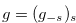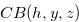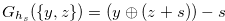Therefore we have a necessary and sufficient condition for the chocolate bar $CB(h,y,z)$ to have the Grundy number $G_{h_ s}(\{ y,z\} ) = (y \oplus (z+s))-s$.

Next an example of this condition is presented for the function 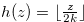$h(z)=\lfloor \frac{z}{2k}\rfloor $. As you see, this condition is quite simple for this function.

Corollary 4.1. Let 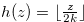$h(z)=\lfloor \frac{z}{2k}\rfloor $ for a fixed natural number 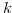$k$. Then

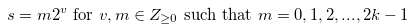  \begin{equation} \label{condiofs} s = m2^{v} \text { for } v,m \in Z_{\geq 0} \text { such that } m = 0, 1, 2,...,2k-1 \end{equation}   (4.26)

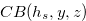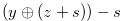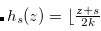if and only if the Grundy number of $CB(h_ s,y,z)$ is $(y\oplus (z+s)) -s$, where $h_ s(z) = \lfloor \frac{z+s}{2k}\rfloor $.

Proof. By Lemma 3.1, the function 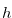$h$ satisfies the conditions of Definition 3.2. By Lemma 4.1,

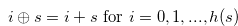  \begin{equation} i \oplus s = i+s \text { for } i = 0,1,...,h(s) \nonumber \end{equation}    

if and only if there exists 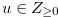$u \in Z_{\geq 0}$ such that

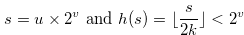  \begin{equation} s=u \times 2^ v \text { and } h(s) = \lfloor \frac{s}{2k}\rfloor < 2^ v \nonumber \end{equation}    

if and only if Condition (4.26) is valid. Therefore by Theorem 4.1 we finish the proof of this corollary.

[1]

S. Nakamura and R. Miyadera, Impartial Chocolate Bar Games, Integers Volume 15, 2015.

[2]

A.C.Robin, A poisoned chocolate problem, Problem corner, The Mathematical Gazette Vol. 73, No. 466 (Dec., 1989), pp. 341-343. An Answer for the above problem is in Vol. 74, No. 468, June 1990, pp. 171-173.

[3]

D.Zeilberger, Three-Rowed CHOMP, Adv. Applied Math Vol. 26 (2001), pp. 168-179.

[4]

M. H. Albert, R. J. Nowakowski and D. Wolfe, Lessons In Play, A K Peters, p-139.

[5]

A.N.Siegel, Combinatorial Game Theory (Graduate Studies in Mathematics), American Mathematical Society (2013).

HOME