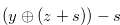4.1 A Sufficient Condition for a Chocolate Bar to have the Grundy Number 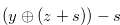
Let 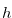 be the function that satisfies the condition
be the function that satisfies the condition 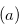 in Definition 3.2 and let
in Definition 3.2 and let 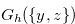 be the Grundy number of
be the Grundy number of 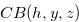 . The condition
. The condition 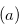 in Definition 3.2 is a necessary and sufficient condition for
in Definition 3.2 is a necessary and sufficient condition for 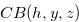 to have the Grundy number
to have the Grundy number  , and we can use all the lemmas and theorems in previous sections for the function
, and we can use all the lemmas and theorems in previous sections for the function 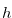 and
and 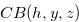 .
.
Definition 4.1. We define the function 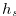 as the followings.
as the followings.
Let 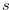 be a natural number such that
be a natural number such that
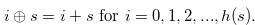 |
Let 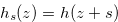 for any
for any 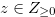 .
.
We are going to show that the condition in Definition 4.1 is a necessary and sufficient condition for the chocolate bar 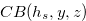 to have the Grundy number
to have the Grundy number 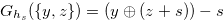 .
.
Lemma 4.1. Let 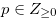 and
and 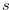 be a natural number. Then
be a natural number. Then
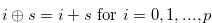 |
(4.5) |
if and only if there exist a natural number 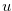 and a non-negative integer
and a non-negative integer 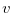 such that
such that
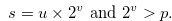 |
(4.6) |
Proof. We suppose Relation (4.5). When  , let
, let 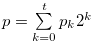 with
with 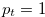 and
and 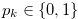 . Let
. Let 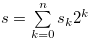 with
with  and
and 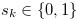 . Since
. Since 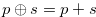 and
and 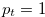 ,
, 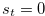 . Since
. Since 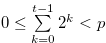 ,
, 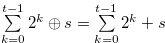 . Therefore,
. Therefore, 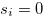 for
for 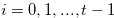 . Let
. Let 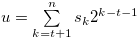 and
and 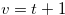 , then we have Relation (4.6). When
, then we have Relation (4.6). When 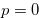 , we let
, we let 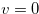 and
and 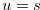 . Then we have Relation (4.6).
. Then we have Relation (4.6).
Next we suppose that there exist a natural number 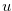 and a non-negative integer
and a non-negative integer 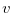 that satisfy Relation (4.6). Then it is clear that we have Relation (4.5).
that satisfy Relation (4.6). Then it is clear that we have Relation (4.5).
Lemma 4.2. Let 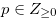 and
and 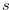 be a natural number such that
be a natural number such that 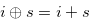 for
for 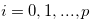 . Let
. Let 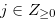 such that
such that 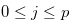 . Then
. Then
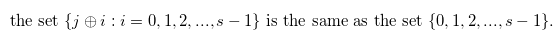 |
(4.7) |
Proof. By Lemma 4.1, there exist a natural number 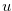 and a non-negative integer
and a non-negative integer 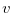 such that
such that 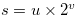 and
and 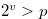 .
.
Let 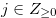 such that
such that 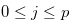 . Then we write
. Then we write 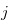 in base 2, and we have
in base 2, and we have 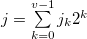 . We prove that
. We prove that 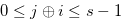 for
for 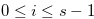 . Let
. Let 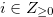 such that
such that
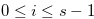 . Then there exist
. Then there exist  such that
such that 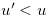 and
and 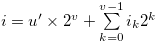 for
for 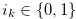 . Therefore,
. Therefore,
 |
(4.8) |
Since 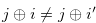 for
for 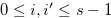 such that
such that 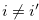 , the inequality in (4.8) implies Relation (4.7).
, the inequality in (4.8) implies Relation (4.7).
Lemma 4.3. Let 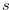 be a natural number,
be a natural number, 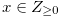 and
and 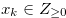 for
for 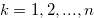 . Suppose that
. Suppose that 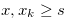 for
for 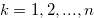 . Then
. Then  if and only if
if and only if 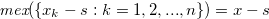 .
.
Proof. Suppose that  . By Lemma 1.1,
. By Lemma 1.1, 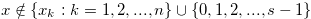 , and hence
, and hence 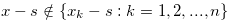 . Let
. Let 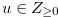 such that
such that 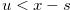 . Then
. Then 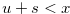 , and Lemma 1.1 implies
, and Lemma 1.1 implies  . Clearly
. Clearly 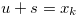 for some natural number
for some natural number 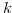 , and hence
, and hence 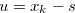 . By Lemma 1.1, we have
. By Lemma 1.1, we have 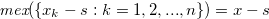 .
.
Conversely we suppose that 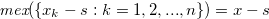 . Then, Lemma 1.1 implies
. Then, Lemma 1.1 implies 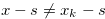 for any
for any 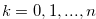 , and hence
, and hence 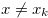 for any
for any 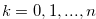 . For any
. For any 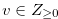 such that
such that 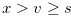 , Lemma 1.1 implies that there exists
, Lemma 1.1 implies that there exists 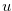 such that
such that 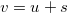 and
and  . By Lemma 1.1, there exists
. By Lemma 1.1, there exists 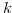 such that
such that 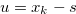 , and hence we have
, and hence we have 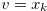 . Therefore Lemma 1.1 implies
. Therefore Lemma 1.1 implies  .
.
Lemma 4.4. Let 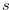 be a natural number such that
be a natural number such that
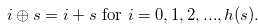 |
(4.9) |
Then, for any 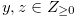 such that
such that 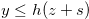 , we have
, we have
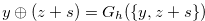 |
|||
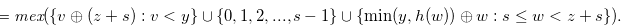 |
(4.10) |
In particular 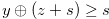 .
.
Proof. By Theorem 3.2 and the definition of Grundy number,
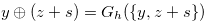 |
|||
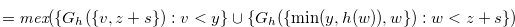 |
|||
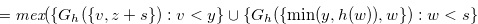 |
|||
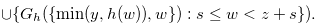 |
(4.11) |
When 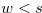 , we have
, we have 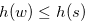 , and hence
, and hence 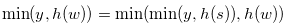 . Since
. Since 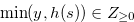 and
and 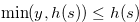 , Lemma 3.10, Equation (4.9) and Lemma 4.2 imply
, Lemma 3.10, Equation (4.9) and Lemma 4.2 imply 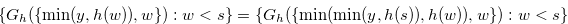
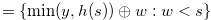
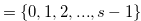 . Hence, by Theorem 3.2,
. Hence, by Theorem 3.2,
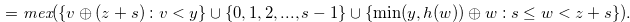 |
(4.12) |
Equation (4.11) and Equation (4.12) imply Equation (4.10). Therefore, by Lemma 1, we have 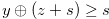 .
.
Lemma 4.5. Let 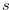 be a natural number such that
be a natural number such that
 |
(4.13) |
For any 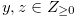 such that
such that 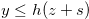 , we have
, we have
 |
(4.14) |
Proof. By Relation (4.13) and Lemma 4.4, we have 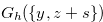
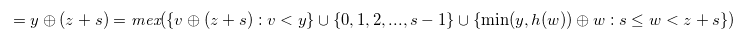 |
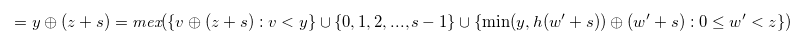 |
(4.15) |
for any 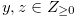 such that
such that 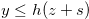 .
.
Since 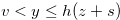 , Lemma 4.4 implies that for
, Lemma 4.4 implies that for 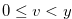
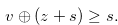 |
(4.16) |
Since  , Lemma 4.4 implies that for
, Lemma 4.4 implies that for 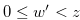
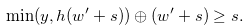 |
(4.17) |
Lemma 4.3, the inequality in (4.16), the inequality in (4.17) and Equation (4.15) imply (4.14). We have completed the proof.
Theorem 4.1. Let 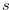 be a natural number such that
be a natural number such that
 |
(4.18) |
and 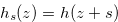 for any
for any 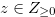 . Let
. Let 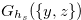 be the Grundy number of
be the Grundy number of 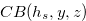 . Then
. Then 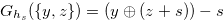 for any
for any 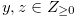 such that
such that 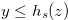 . Let
. Let 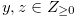 such that
such that 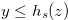 . We prove by mathematical induction, and we assume that
. We prove by mathematical induction, and we assume that 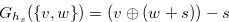 for
for 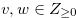 such that
such that 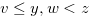 or
or  .
.
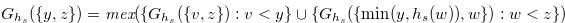 |
|||
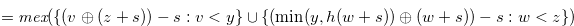 |
|||
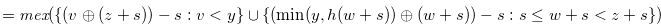 |
|||
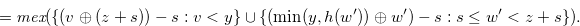 |
(4.19) |
By Lemma 4.5,  , and hence we finish this proof.
, and hence we finish this proof.