我々はここまでの節においてGrundy数がG({y,z})=y ⊕ zを満たすチョコレートCB(f,y,z)についての研究を行った.その条件G({y,z})=y ⊕ zを部分的に変えることにより条件G({y,z}) = (y ⊕ (z+s))−s (但しsは自然数の定数)を得た.
この節において我々はGg({y,z}) = (y ⊕ (z+s))−s (但しsは自然数の定数)を満たすチョコレートCB(g,y,z)の必要十分条件について研究した.
例 3.1
補題 2.1及び定理 2.2より図 3.1のチョコレートのGrundy数は
ここで
であるが, 定理3.1 (この定理の証明はこの論文の後の方で行われている.)より図3.2のチョコレートのGrundy数は
|
Gf12({y,z})=(y ⊕ (z+12))−12
(81) |
となる.なお, ここで
とする.
等式(79)と(81)の違い及び,等式(80)と(82)の違いに注目して欲しい.
図3.2のチョコレートは図3.1のチョコレートの苦い部分を水平に動かし, 垂直に切ることで生成されるものであることは容易に理解できる. その作成方法を図 3.3に示す.
この方法を一般化したとき,チョコレートCB(
g,
y,
z)
におけるGrundy数がGg({
y,
z}) = (
y ⊕ (
z+
s))−
s(但しsは自然数の定数)を満たす必要十分条件を得ることができる.
CB(
f,8,32)
f(
t)
= ⌊
t/4⌋
図 3.1
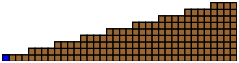
CB(
f12,8,23)
f12(
t)=
f(
t+12)= ⌊
t+12/4 ⌋
図 3.2
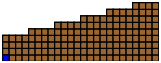
図 3.3

例3.1にあるように,Grundy数がGfs({y,z}) = (y ⊕ (z+s))−sを満たすチョコレートはGrundy数がGf({y,z})=y ⊕ zを満たすチョコレートから作ることができる.
初めに十分条件を研究する.


