暗号化する鍵と復号する鍵が同じ鍵を使う暗号方式。その鍵のことを共通鍵という。
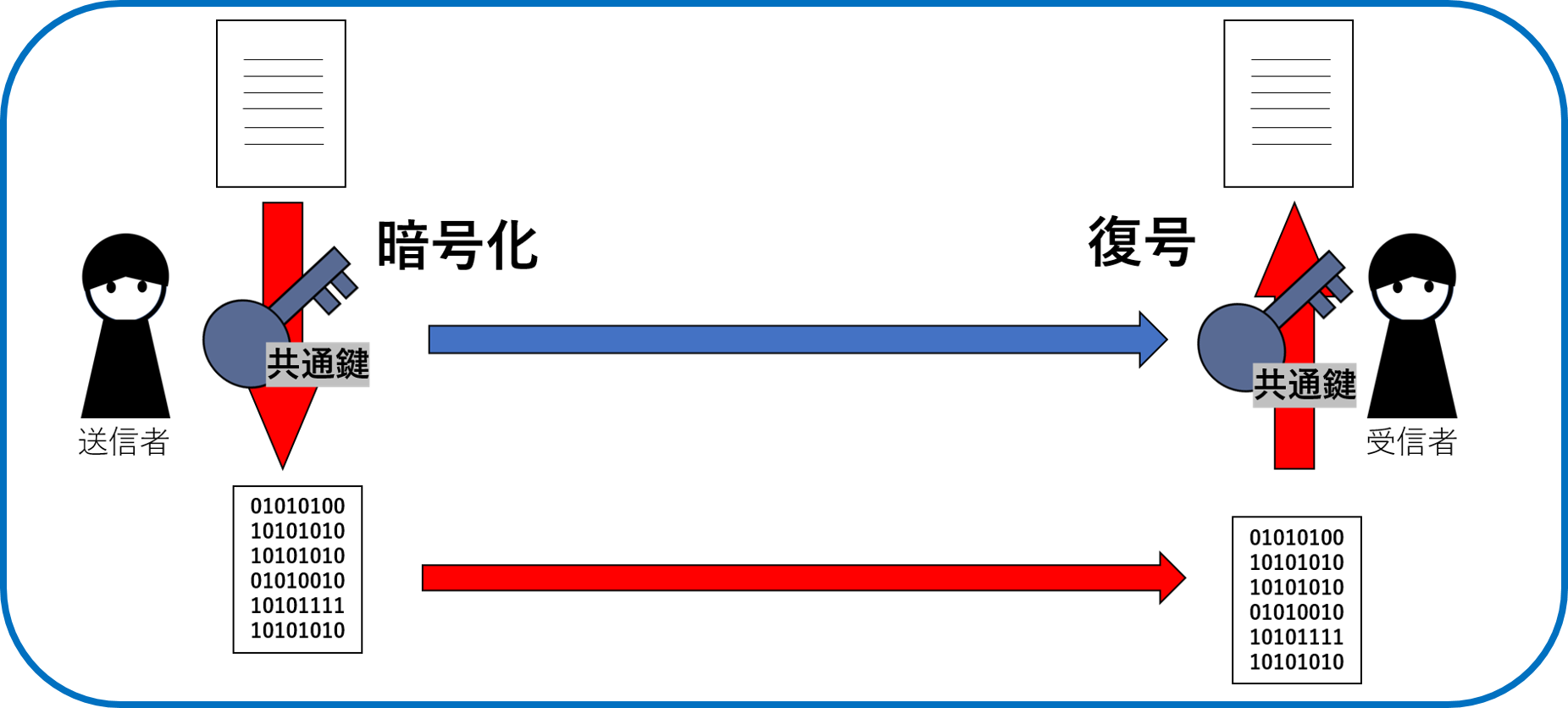
特徴
・データの処理時間が速い。
・共通鍵がわかるとデータが復号され、やり取りの内容が盗み見られてしまう。
・やり取りの相手ごとに共通鍵の作成が必要。
・共通鍵暗号で使用するアルゴリズムの規格にはRC4、DES、3DES、AESがある。
1987年にRivestにより開発されたストリーム暗号。
1ビット単位で暗号化・復号が可能な暗号。
鍵長は40ビットから2048ビットまでの範囲で選択することができる
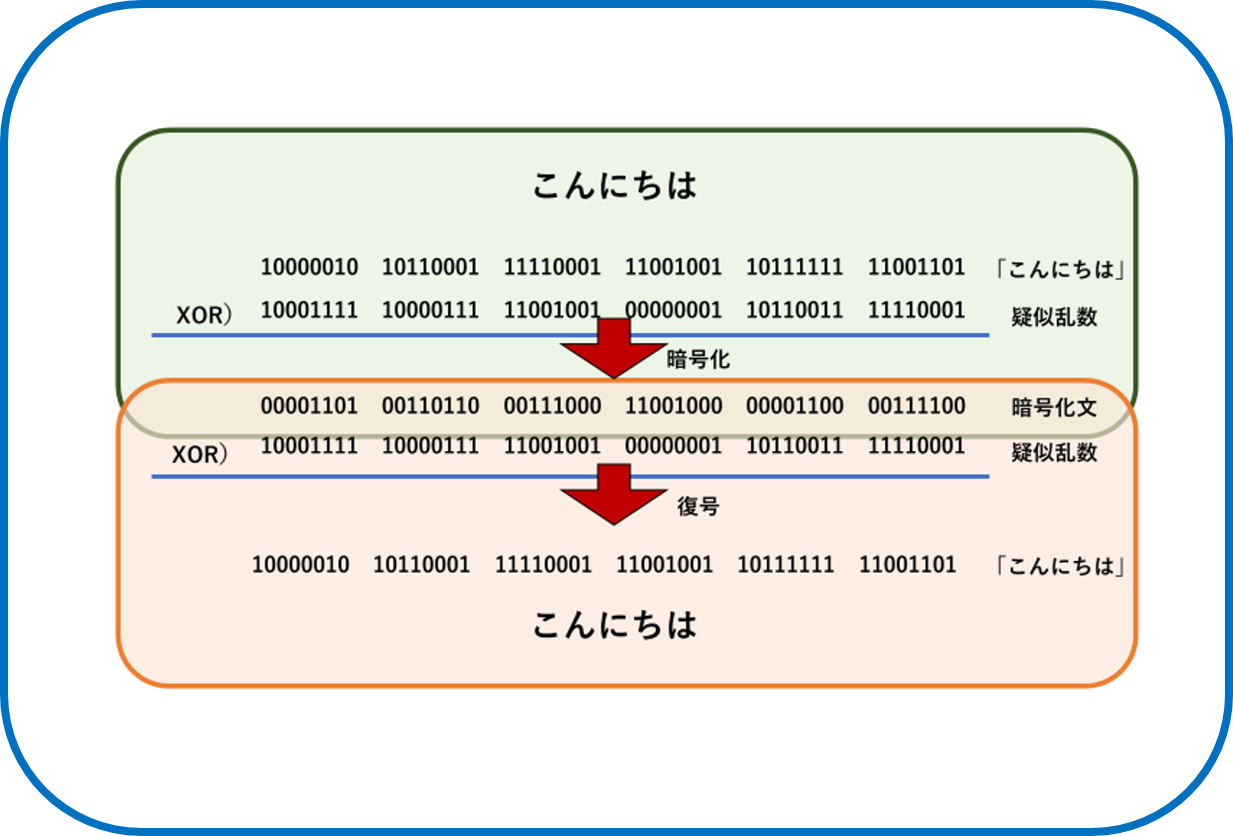
１.文章をビット化
２.暗号鍵を元に擬似乱数列の生成
３. 1ビットずつのXOR（排他的論理和）をして暗号化する
1.暗号化に使った疑似乱数と1ビットずつのXOR（排他的論理和）をする
2.ビットを文章に直す
セキュリティ上の脆弱性が発見され、 RC4を使用した暗号通信は特定の攻撃手法によって解読される可能性が高いため現在では使用がされていない。
より安全なAES（Advanced Encryption Standard）などの暗号方式が推奨されている。
1977年 アメリカ連邦政府標準規格として採用された暗号方式。
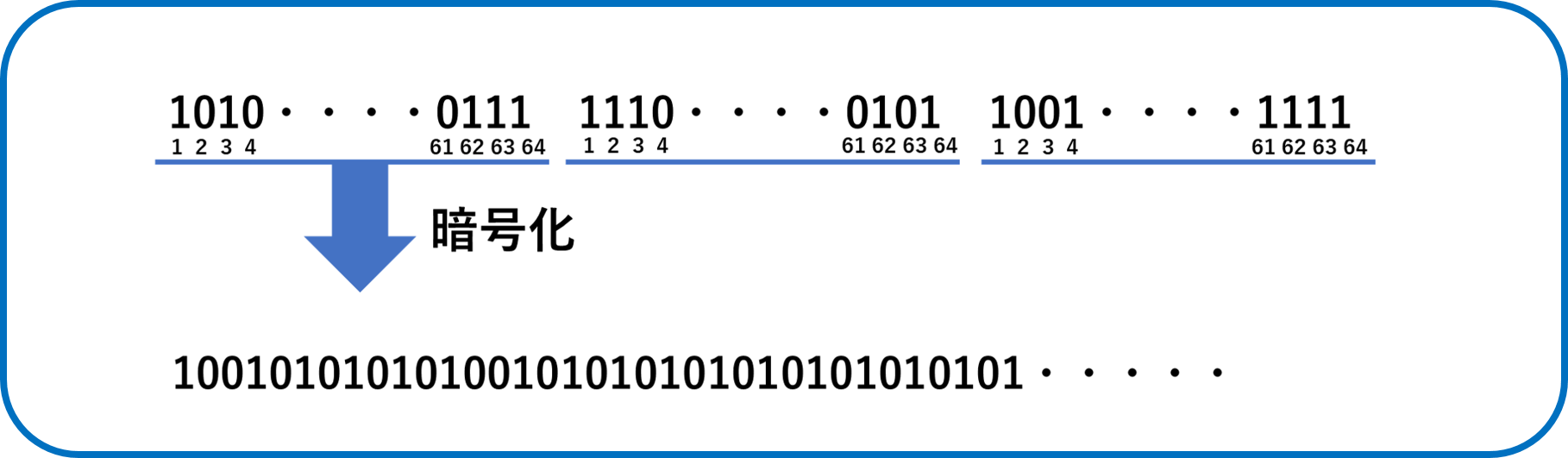
データを64ビット単位に区切って処理するブロック暗号である。
(ブロック暗号 データをある長さに区切って暗号化するもの。)
鍵長の56ビットにパリティチェック用の8ビットを加えた64ビットを鍵データとして管理する。
パリティチェック データの送信が適切に行われたかを確認するもの。
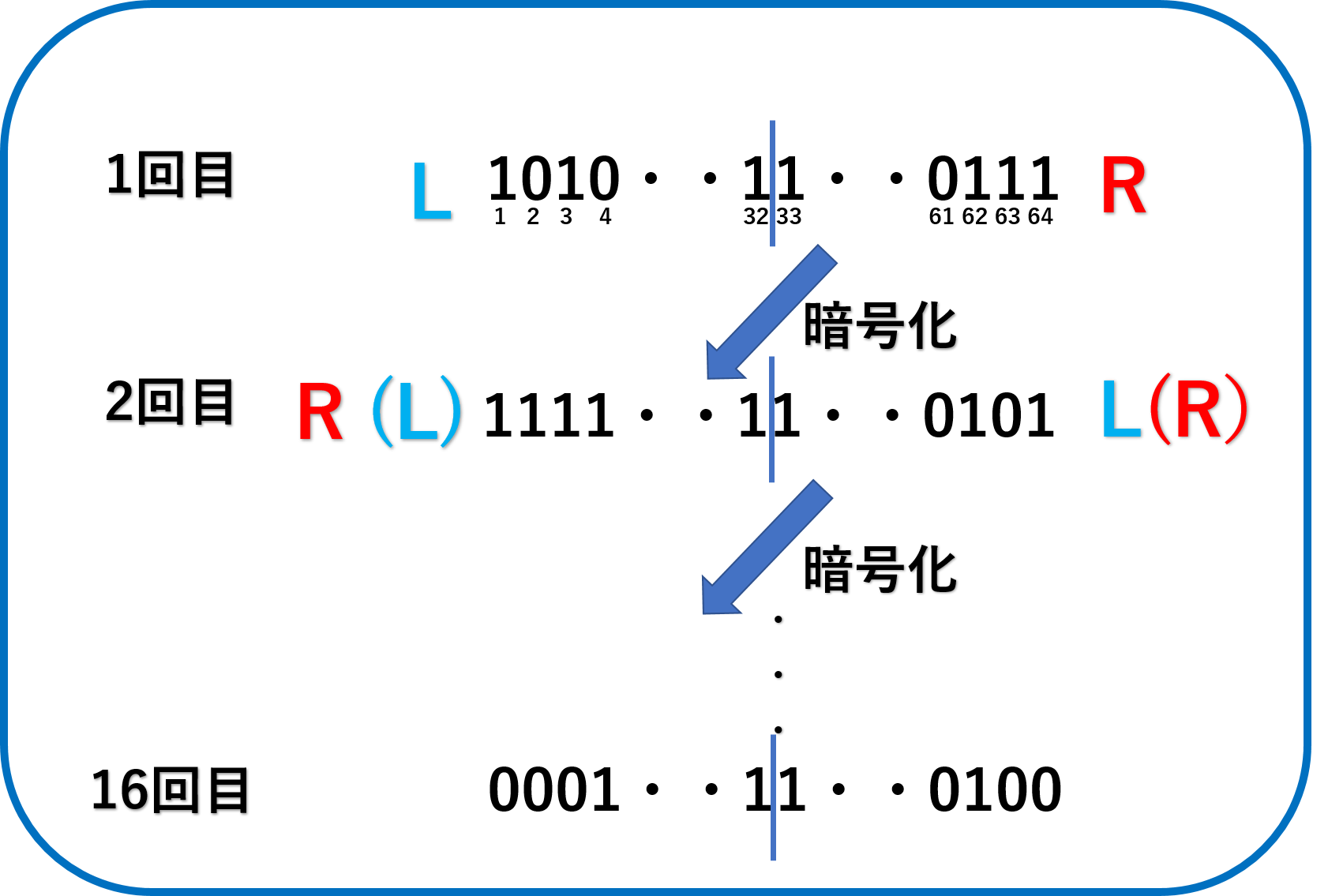
1.データを32ビットずつ半分に分割
2.一回のラウンドでは半分（R）を変換
3.残りの半分（L）と合成する
4.Rを新たなLとする
5.この一連の処理(ラウンド)を16回繰り返し行う
データ全体を一度にまとめて処理せず、１回の処理の負担が軽いのが特徴。
1977年 策定された共通鍵暗号の規格。
DESの脆弱性の発見後
それまでDESのみに対応した処理系が多かったため、応急的に安全性を高める方式として考案されたもの。
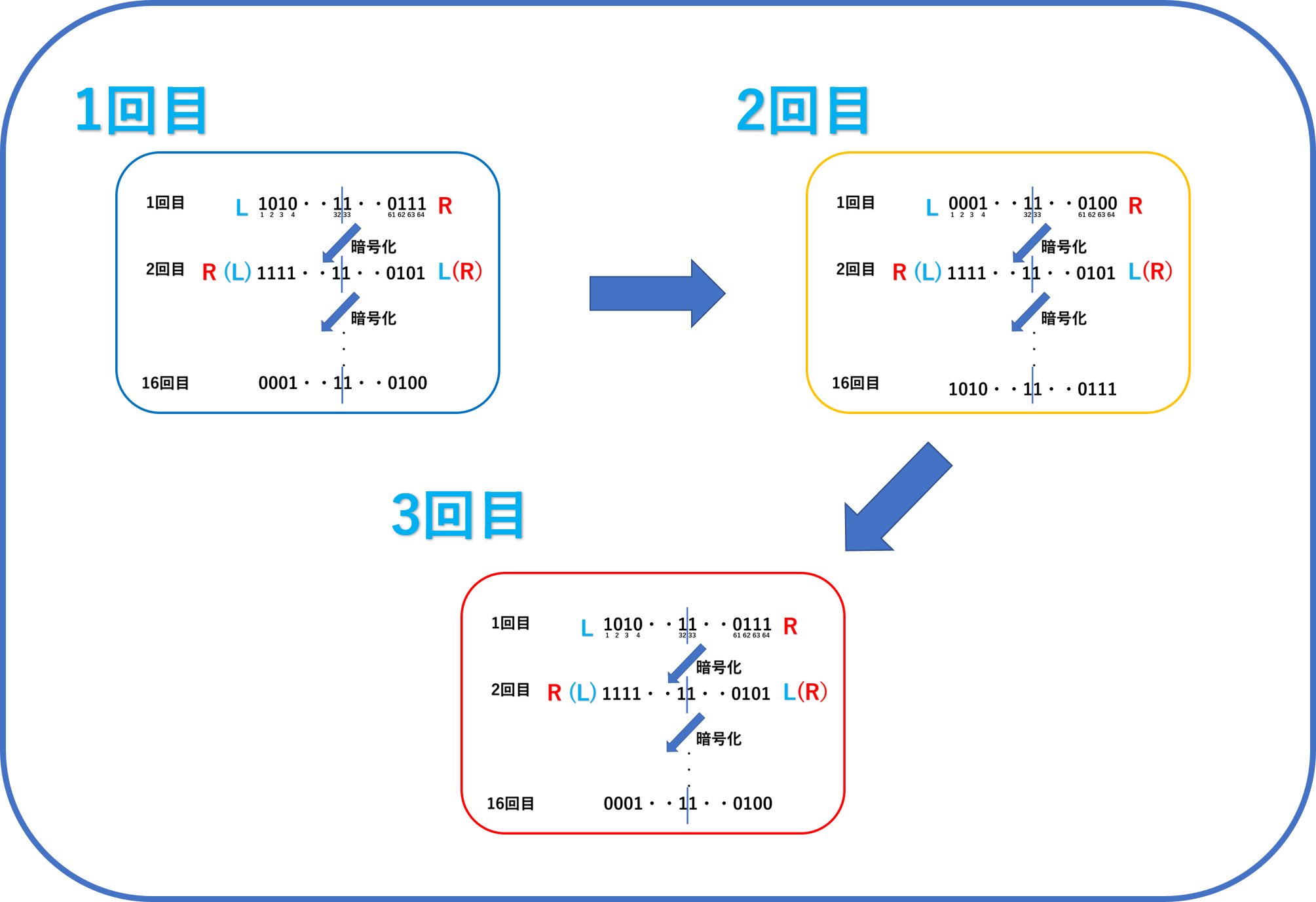
異なる2つまたは3つの暗号鍵を用いて、DESによる暗号化と復号の処理を3回繰り返すことにより、解読されにくくする方式。
特徴
・DESより安全性は格段に高い。
・暗号化・復号に長い時間がかかる。
2001年
アメリカ連邦政府標準の暗号方式として採用された、共通鍵暗号方式。
現在の主流となっている
開発元の許諾や対価の支払いが必要な特許技術などを含まず、完全な仕様が公開され、誰でも自由に利用することができる。
有効な攻撃手法は見つかっておらず、高い安全性を誇る。
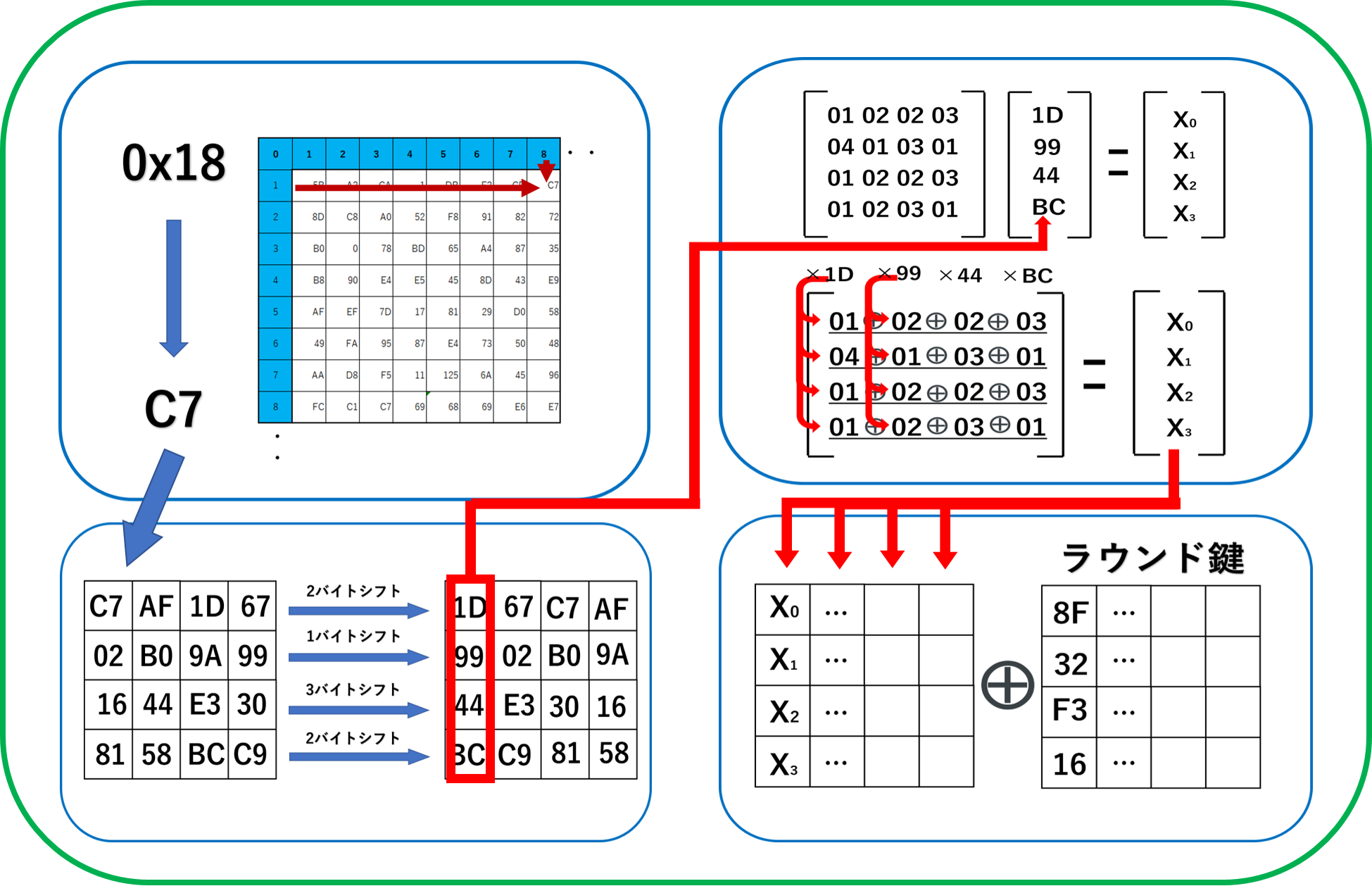
文字データの変換
変換したデータを4×4の2次元配列に格納
行ごとに左にバイトシフト移動
行列変換
ラウンド鍵とXOR演算
(1ラウンドごとに生成される鍵)
この一連の処理(ラウンド)を繰り返し行う
鍵長が128ビット：10ラウンド
192ビット：12ラウンド
256ビット：14ラウンド行う
特徴
・AESの鍵長は128・192・256bitから選択可能で、DESより長く安全性が高い。
・処理速度が速い
無線LAN（Wi-Fi）の通信の暗号化、インターネット上の通信を暗号化するSSL/TLS、圧縮ファイルの暗号化などで用いられている。
様々な製品や技術規格などに採用され、共有鍵暗号の標準として全世界で広く普及している。
共有鍵暗号方式の共通鍵の配送に光ファイバーを用いた量子経路で送る量子力学の不確定性原理 を応用した暗号方式。
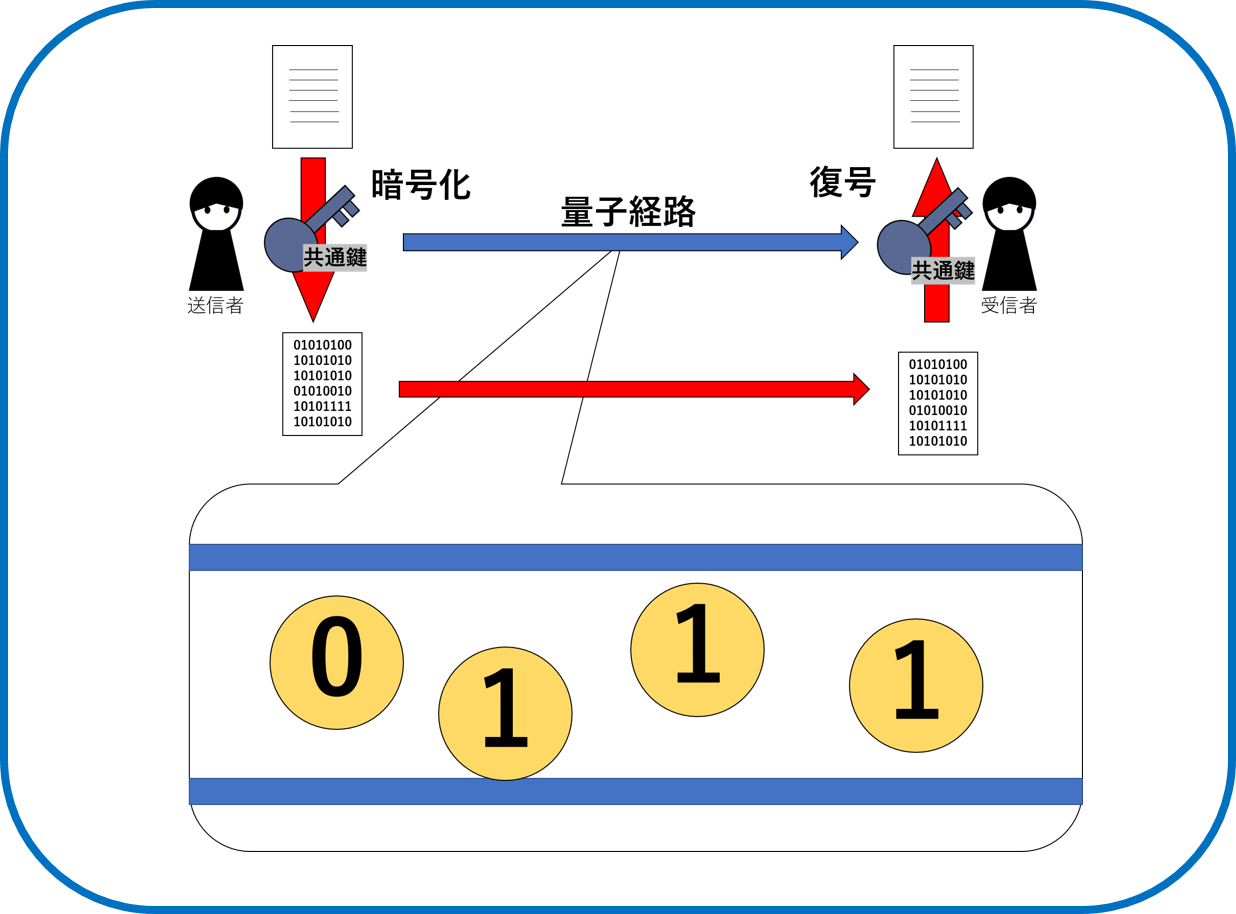
情報が盗聴された際、量子の持つデータに変化が起こる。それが検知されたら盗聴され共通鍵を破棄し新しい共通鍵を作成しを送る。そのため、とても安全にデータのやり取りをすることができる。
量子もつれによる脆弱性
量子暗号に使われる光源では、擬似単一光子光源が使われている。
実際には単一ではなく2個以上の光子がある程度の確率で発生してしまう。
余分に発生した光子を観測することで、痕跡を残さず秘密鍵を盗聴できるとされている。
伝送距離を延ばすのが困難
量子経路に中間地点を設けることや、光子をいったん電子に乗せ換えるなどの工夫で通信距離を伸ばそうとする研究が進んでいる。
暗号化する鍵と復号する鍵で異なる鍵を使う暗号方式。 その鍵のことをそれぞれ公開鍵、秘密鍵という。
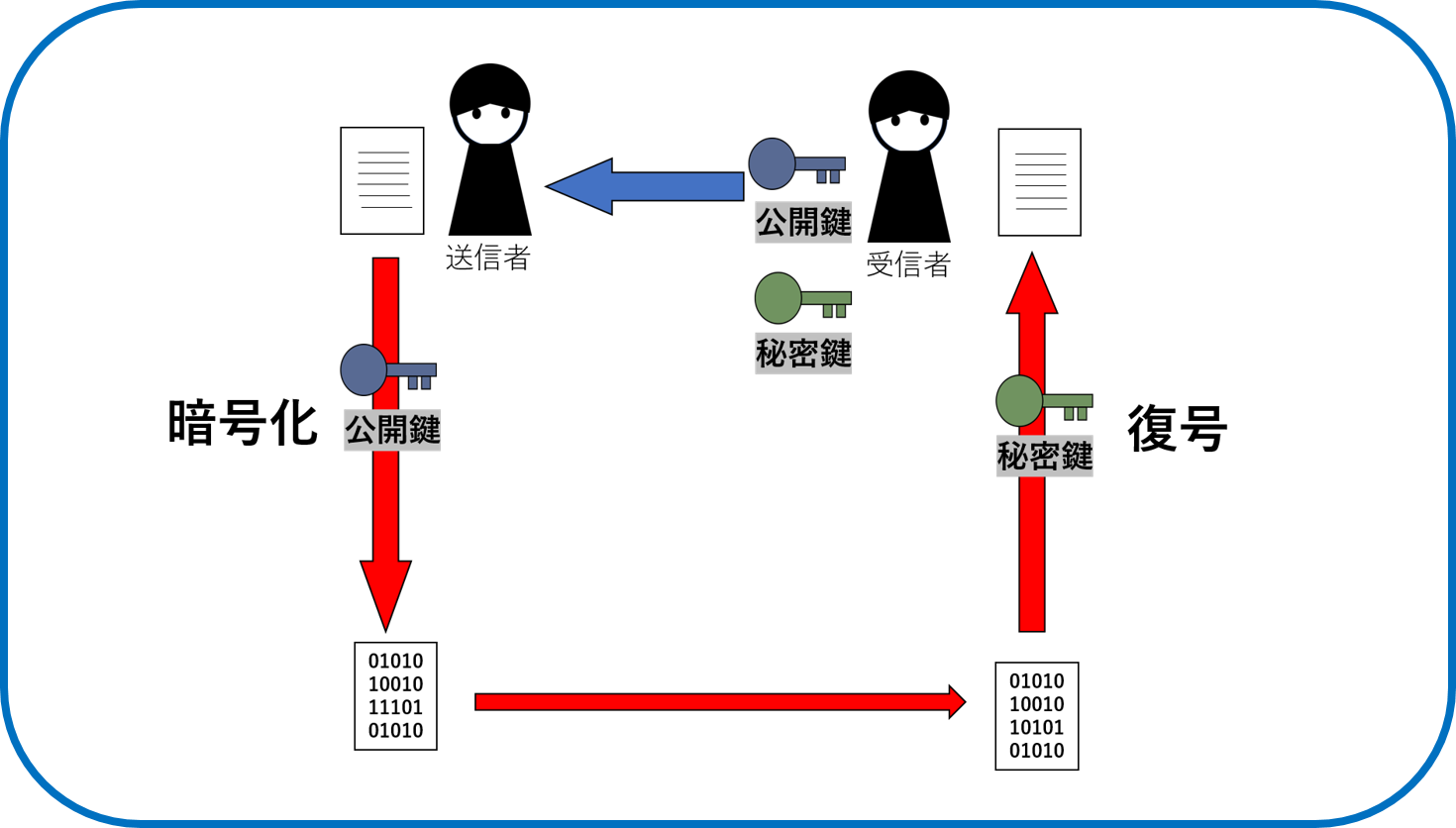
公開鍵暗号で使用するアルゴリズムには ElGamal、DSA、ECDSA 、RSAがある。
特徴
・データの処理に時間がかかる。
・1つの鍵で複数の相手とやり取りできる。
・公開鍵がわかってもデータの復号ができない。
1985年
エジプト人暗号学者タヘル・エルガマル（Taher A. Elgamal）氏によって開発された。
離散対数問題と呼ばれる数学の問題を応用し秘密鍵が推測されないようにした公開鍵暗号。
素数aと整数b,cを公開鍵、ｘを秘密鍵としたときｘを求めるにはしらみつぶしに計算しないといけないので計算量が多くなる
RSA方式などに比べ短い鍵長で高い安全性が得られるため、鍵交換アルゴリズム（ECDH）やデジタル署名として広く普及している。
楕円曲線上の離散対数問題と呼ばれる数学上の問題を利用したデジタル署名方式。
DSAは、2048ビットや3072ビットの鍵長に対しECDSAはその10分の１程度の長さで同等の安全性を実現することができる。
ElGamalの改良版で、アメリカ政府標準のデジタル署名アルゴリズムとして採用されている。
送信メッセージのハッシュ値と秘密鍵を含む計算によりデジタル署名を生成してメッセージに添付する。
公開鍵を取り寄せて検算を行い署名が正しいかを見て改ざんされていないことを確かめることができる。
正しい署名を偽造するには秘密鍵（自然数）を割り出さなければならないが、効率よく探索する手法は未だ発見されていない。
二つの巨大な素数同士の積を素因数分解するのが困難であることを利用した公開鍵暗号。
RSAは初めて実用化された公開鍵暗号方式として、通信ネットワーク上の暗号化やデジタル署名に幅広く普及し、Web通信の暗号化などに用いるSSLやTLSなど、多くの標準規格の一部に採用されている。
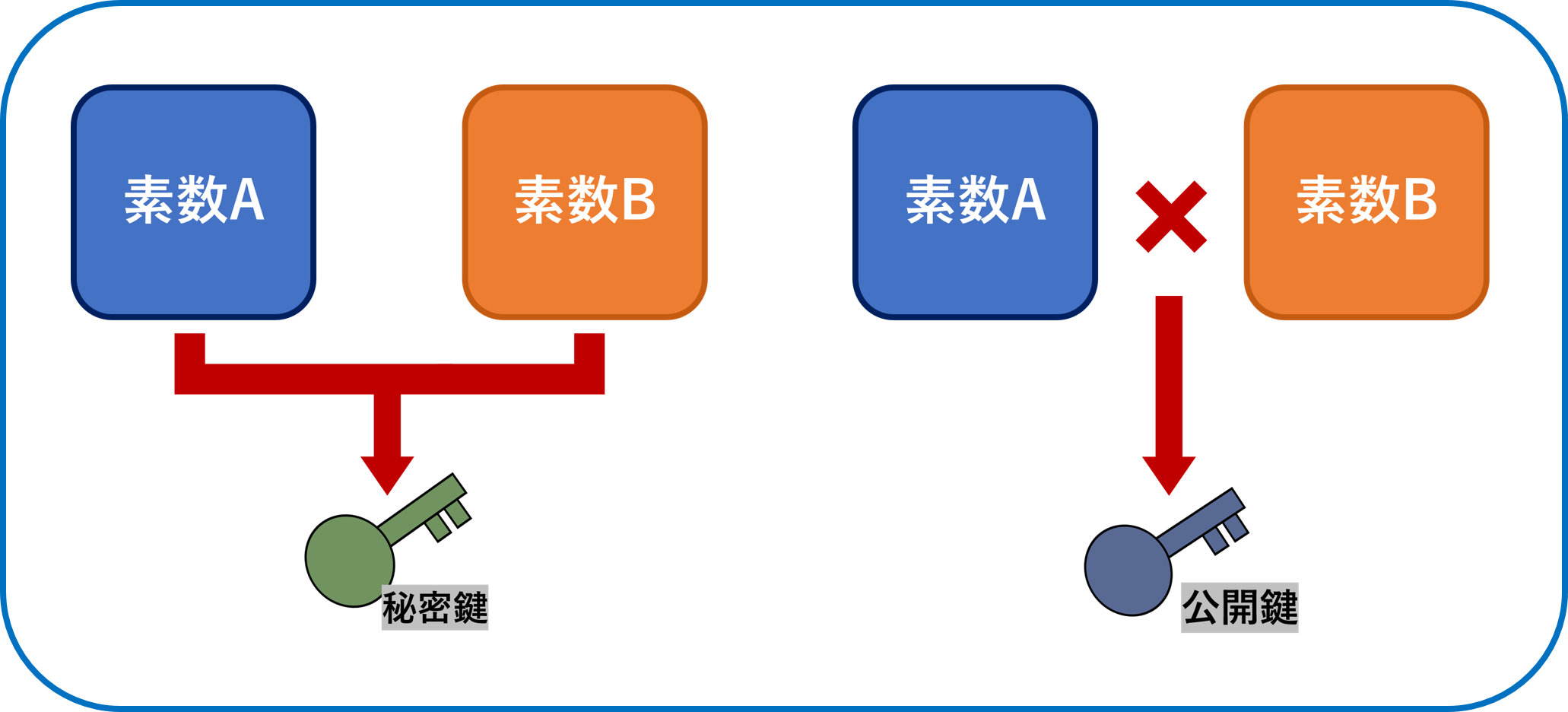
二つの巨大な素数を生成し、二つの素数を元に秘密鍵を、素数の積を元に公開鍵を生成する。
公開鍵を入手しても対になる秘密鍵を割り出すのは困難となる。
鍵生成のために大きな桁数の素数を発見するのは時間がかかるため、実際には簡易な判定手法を用いて素数である確率が高い数（確率的素数）を見つけ出し、利用する。
共通鍵暗号方式と公開鍵暗号方式を組み合わせたもの。
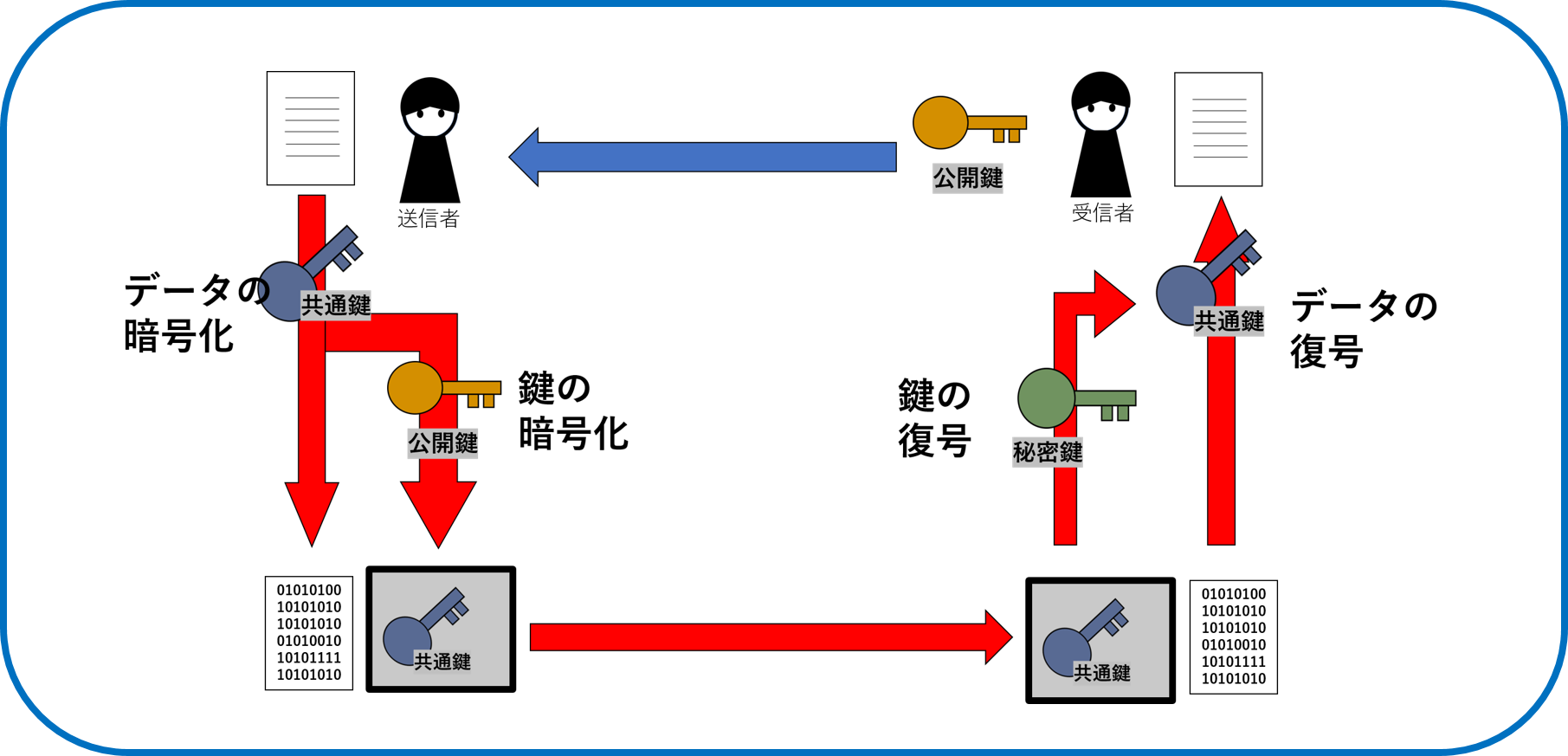
・共通鍵を公開鍵で暗号化し暗号文と一緒に転送する。
・秘密鍵で暗号化した共通鍵を復号しその共通鍵で暗号文を復号する。
・データの処理に時間がかからない。
・公開鍵がわかってもデータの復号ができない。
・Webの暗号化などで広く普及しているSSL/TLSなどで用いられている。
共通鍵暗号と公開鍵暗号の長所を活かして互いの短所を補い合っている。
