標準偏差
度数分布表やヒストグラムなどのグラフでデータの分布を確認したけれど、それを数値化することもできるんだ。

え、そうなの!?
それは標準偏差という値なんだ。

何それ?
もしかして偏差値とかって…標準偏差が関係あるんですか?
そうだ。模試とかをしているといつも記されてるだろう。

いつも偏差値50超えているかが不安になる…
偏差値50も良い着眼点だね!では標準偏差の仕組みと求め方を教えよう。ではその基礎となる偏差と分散、そして標準偏差について説明しようか。

偏差
偏差とは、平均値からの差を表し、データの値から平均値を引くことで求めることができる。正の偏差の場合、平均よりも値が大きく、逆に負の偏差の場合は平均より値が少ない。※下の図は例としてAからEさんが100点満点である情報のテストを受けたときの結果であり、平均点を75点とする。
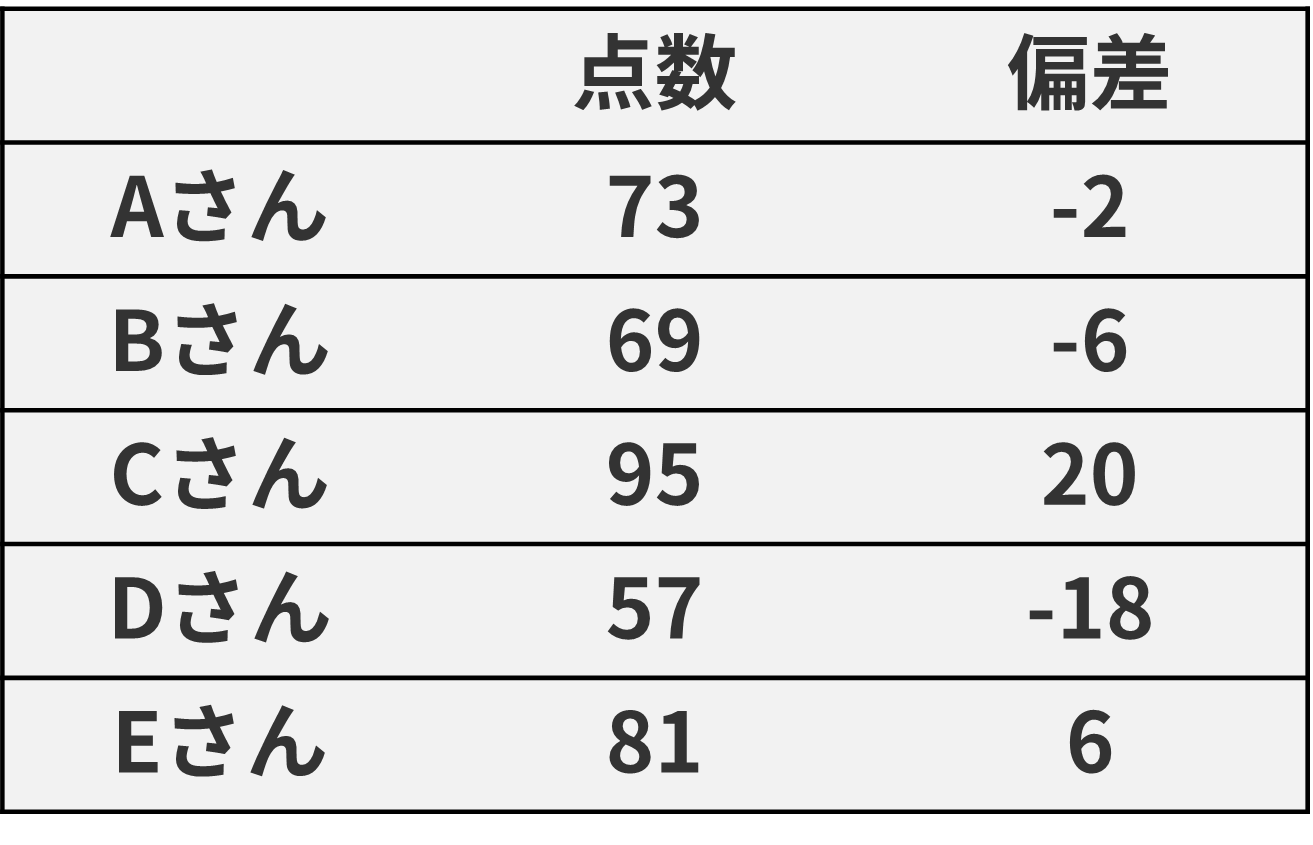
分散
分散とは、データの散らばりの具合を表し、それぞれ偏差を2乗した値を足してデータの個数を割った値である。先ほどの図から分散を求める場合、このような計算になる。分散が0に近いときは散らばりは小さく、逆に0から離れているときは分散が大きい。
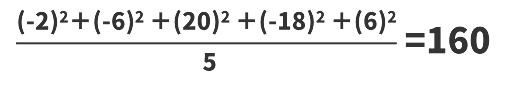
標準偏差
標準偏差は分散と同じくデータの散らばりの具合を表すが、分散の場合答える単位が二乗となってしまう問題がある(cm2g2など)。そのため、標準偏差では「√分散」とすることで元の単位に戻している。実際に先ほどの分散を求めた式を標準偏差に戻すと図のようになる。
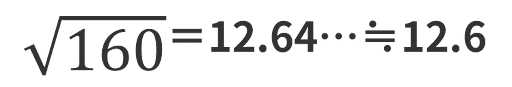
つまり散らばり具合を調べるときはこの順番で計算すると良いよ。

①データの平均値を求める
②データの偏差を求める
③データの分散を求める
④データの標準偏差を求める
探Q
あれ?なんでわざわざ分散を求めるときに偏差を二乗するんですか?偏差を二乗しなければ標準偏差の手間が省けると思うんですけど...
フッフッフ...それには理由があるんだよ...

分散を求めるときに偏差を二乗する理由
偏差をただ足し合わせて平均を求めると、偏差が平均値からの距離をあらわすことから必ず値が0になる。そのため正確に分散を求めることができなくなってしまう。そこで偏差を二乗することで負の偏差を正の偏差にし、正確に分散を求めることができるようになる。
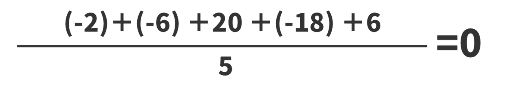
また、同じ平均値でも二乗をすることによってそのデータのばらつきが分かる。例えば、先ほどのデータと同じ平均値をとるデータがあったとしても、偏差が異なる場合は分散も変わっている。このように二乗をすることは平均だけでは見れないデータの特徴を確認することができる。

先程までは分散や標準偏差の計算について記したけど、表計算ソフトでは関数を使えば簡単に求めることができるんだ。

VAR.P関数(分散)
分散を求めるときにはVAR.P関数を使い、=VAR.P(範囲)を使う。VARはpopulation varianceの略であり、母分散(母集団からの分散)を表している。例えば情報の分散を知りたい場合は図のように空白のセルに「=VAR.P(B3:B7)」とすると、B3からB7までの数値の分散を求めることができる。また、sample varianceという標本からの分散を表しているものもある。

STDEV.P関数(標準偏差)
標準偏差を求めるときにはSTDEV.P関数を使い、=STDEV.P(範囲)を使う。STDEVは英語で、standard deviationという意味であり、Pは分散のときと同じく母集団という意味がある。例えば情報の標準偏差を知りたい場合は図のように空白のセルに「=STDEV.P(B3:B7)」とすると、B3からB7までの数値の標準偏差を求めることができる。

うわ!すごく簡単に標準偏差を求めることができたよ!
そうだね、じゃあ標準偏差を求められたから実際に偏差値を求めてみよう。

偏差値
偏差値はこのような公式となっている。

例えば下の図でAさんの偏差値を求める場合、以下のような計算となる。
50+(73-75) ÷ 12.6 × 10 = 48.41…≒48.4
このように平均値や標準偏差などから偏差値を求めることができる。

探Q
そういえば偏差値は50から60、70と上がるとすごいと言われていますがどのくらいすごいのですか?
では偏差値が高いと何がすごいのか教えよう。

偏差値の仕組み
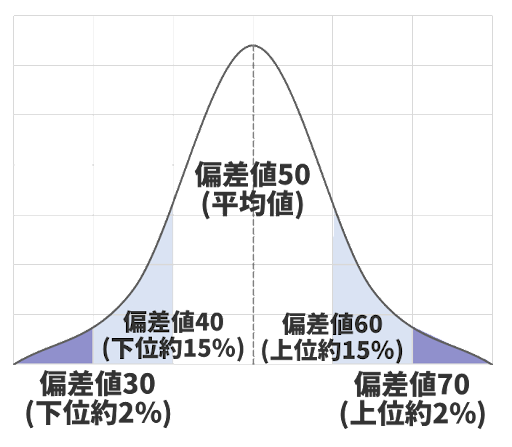
偏差値は平均点を偏差値50として定められており、そこから自分の点数がどのくらい離れているかで決まる。偏差値50は平均点であるため、上位約50%であることがわかる。しかしながら偏差値60は上位約16%、偏差値70は上位約2%まで下がっているのだ。
- ①平均値からの差を偏差、データの散らばり具合を求めることができる分散がある。
- ②標準偏差は「√分散」となっている。
- ②検定にはt検定やカイ二乗検定などがある。

