データの種類
データには箱ひげ図などで表現出来ないものもあるけど、どうして?
実はデータには種類が分かれているんだ。

そうなの!?
大丈夫。ではひとつずつ説明していこう。

質的データ(質的変数)
質的データとは分類や種類が区別されているデータである。例えば、ある問題に対して○と×のカテゴリに分けたり、アンケートでAとBで答えたりする。また、質的データでも名義尺度と順序尺度の2種類に分けることができる。
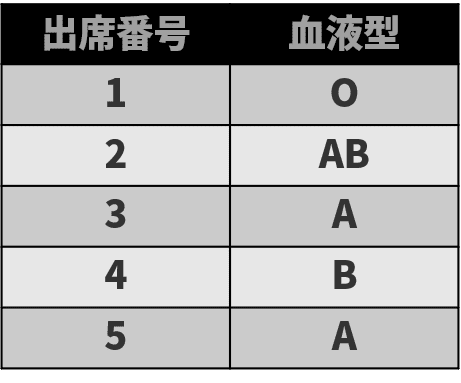
名義尺度
名義尺度とは区別することに意味がある尺度であり、性別や血液型の分類や都道府県の名義分けなどに使われる。例えば、血液型でA型を0、B型を1として分けても数値に大小関係はない。つまり数値や名義に大小関係や順序は無く、名義で分類しているものである。
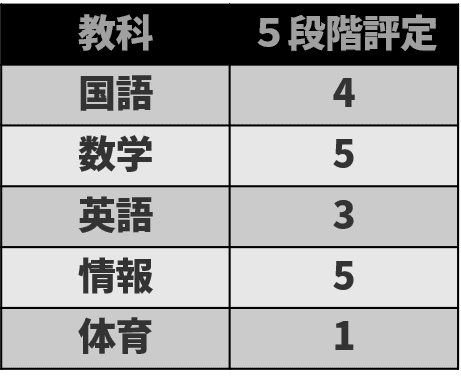
順序尺度
順序尺度とは順序が名義や数値に適応できるデータだが、間隔に意味がないものである。例えば、評定の区別で5,4,3,2,1やランクの区別でA,B,C,D,Eにすることも順序がある。しかし、それらの差の間隔には意味がない。なので最頻値や中央値は求められるが、平均値や合計値は表すことができない(又は意味がない)。
量的データ(量的変数)
量的データとは数値として意味のあるデータであり、足したり引いたり演算ができる数字に意味がある変数。また、質的データとの大きな違いとして量的データは平均値を求めることができる。量的データの中でも2種類に分かれていて間隔尺度と比例尺度がある。
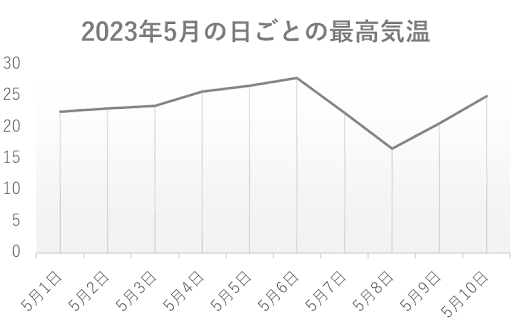
間隔尺度
間隔尺度は目盛の間隔が一定なデータであり、温度やテストの点数などのデータに使われる。間隔尺度では差の大きさでよく比較される(10℃のAと20℃のBで比べるとBがAより10℃高いことになる)ので、加減の計算をすることは出来る。また、0℃や0点のように”0”を存在しないものとせずに”0”を数えるものとする。
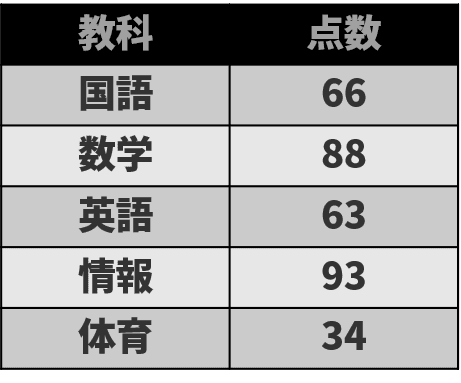
比例尺度
比例尺度とは0を原点としたときに間隔と比率に意味があるデータであり、全ての演算が可能なデータである。間隔尺度とは違い、”0”を存在しないものとする。例えば、身長や速度での”0”は温度やテストの点数の”0”のように具体的に表す事が出来ない。比例尺度では加減の計算をすることが出来ることに加えて、乗算(掛け算)や除算(割り算)が出来る。
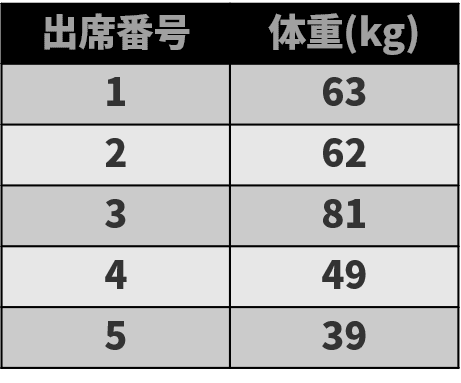
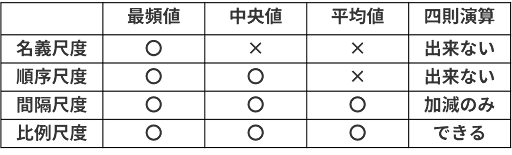
尺度の計算
それぞれの尺度の計算では、比例尺度>間隔尺度>順序尺度>名義尺度の順に計算の自由度が変わっている。