
素因数分解について
君たちは素数というものを知っているよね。

はい。1とその数自身でしか割り切ることができない数のことですよね。
そうだね。では素数かどうか判定するプログラムをPython で実行しようとすると、どんな方法があるかな?

う〜ん、難しいなぁ。素数とそれ以外の数字の違いってなんだろう。
いわゆる合成数というものと素数に分けられるね。合成数は素数の掛け合わせによって作られる数字だよ。簡単な例だと 6 とかも 2×3 で表せて、その2と3は素数だよね。
じゃあ例えば、2を素数に持つ8は当然だけど2で割り切れて、3とか5、 7では割れないよね。つまり合成数を割り切れたら、その割り切れる最小の値と、そもそも合成数を割り切れない値が素数になる、ってことになるよね。
でもそれだと、極端な例を挙げると8を15でわっても割り切れないし、15は素数の3と5を掛け合わせた数字だよね。必ずしも割り切れない数字が素数にはなれないんじゃないかな。

今の例で言うと、8は2を3つ掛け合わせた数なので、そもそも素数に3と5を両方持つ数で割り切ることは不可能だと思います。2を3で割り切れることはできないからです。
そういうことになるよね。つまり何が言いたいかっていうと、素数で合成数を割る時、その割った後の数がまたその素数で割り切れなかったら、別の素数で割れる可能性が高いってことなんだ。順々に割っていくということだね。

一般的に、任意の数nまでの数の中の素数を見つけるには、nをその数の -1までで割って、割り切れなかったら割る数を増やしてその数をまた割って・・・と繰り返す。
これを試し割り法という。
(注意)商が小数になることを許す場合、2,5の二つの素数はどんな数も必ず割り切れる。
Pythonの計算上ではfloatを使わない場合整数の範囲内で終了する。
試し割り法だととある欠点があるよね。そこで考えてほしいこととして、君たちはコンピューターの処理時間はどのくらいかかると思うかい。

あまり時間はかからなかったものだと思いますけど。時間といえば先ほど確認した試し割り法だと時間がかかるように思えます。
まさにその通りなんだ。そこで次に考えられたことに以下のものがある。

(i).整数Nの最大の素因数は√N以下になる。
これって、つまりどういうことなの?
例を挙げたほうがわかりやすいと思うから、見ていこうか。



特に右の数字の方はわかりやすいですね。つまり素数を2乗した数は全て(i)のルールを満たすってことですもんね。
そうだね。このルールが成り立つことによって、素数の列挙を素早くするコツがわかるね。レイさんわかるかな?

つまり、任意の数Nの平方根以下の数までで検証すればいい、ってことかな?
そういうことだね。さらに言うなら、既に素数のみの箱、リストを作ることができたら、その数で判定していけばいいと思わないかい?

それなら聞いたことがあります。確かエラトステネスの篩(ふるい)というものですよね。
エラトステネスの篩(ふるい)
連続していく数たちの中から2の倍数(2を除く)、3の倍数(3を除く)、5の倍数(5を除く)、・・・・・と素数以外を除く、まさに篩にかけているアルゴリズムを古代ギリシャの科学者のエラトステネスが考案したことより生まれた理論。
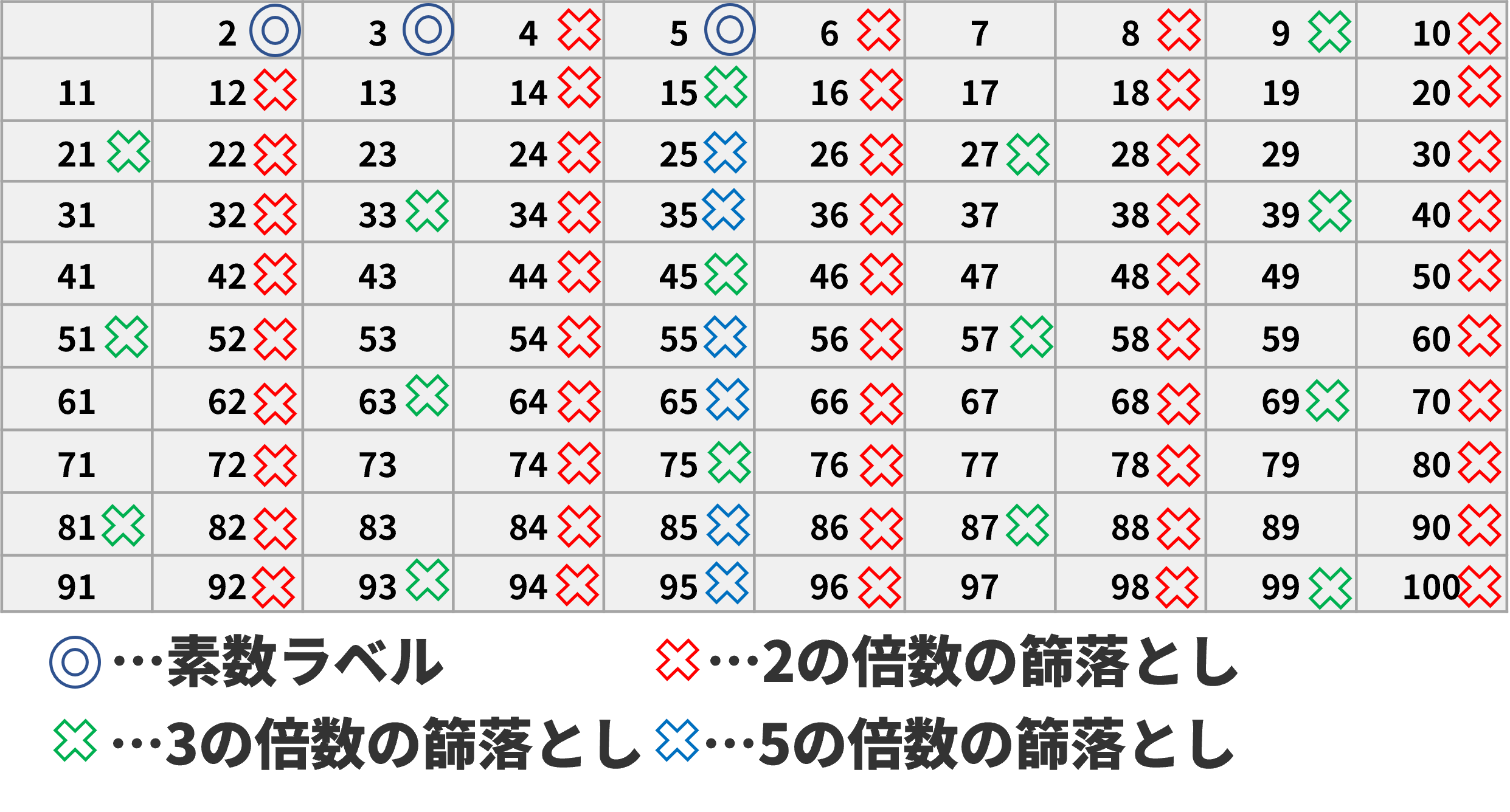
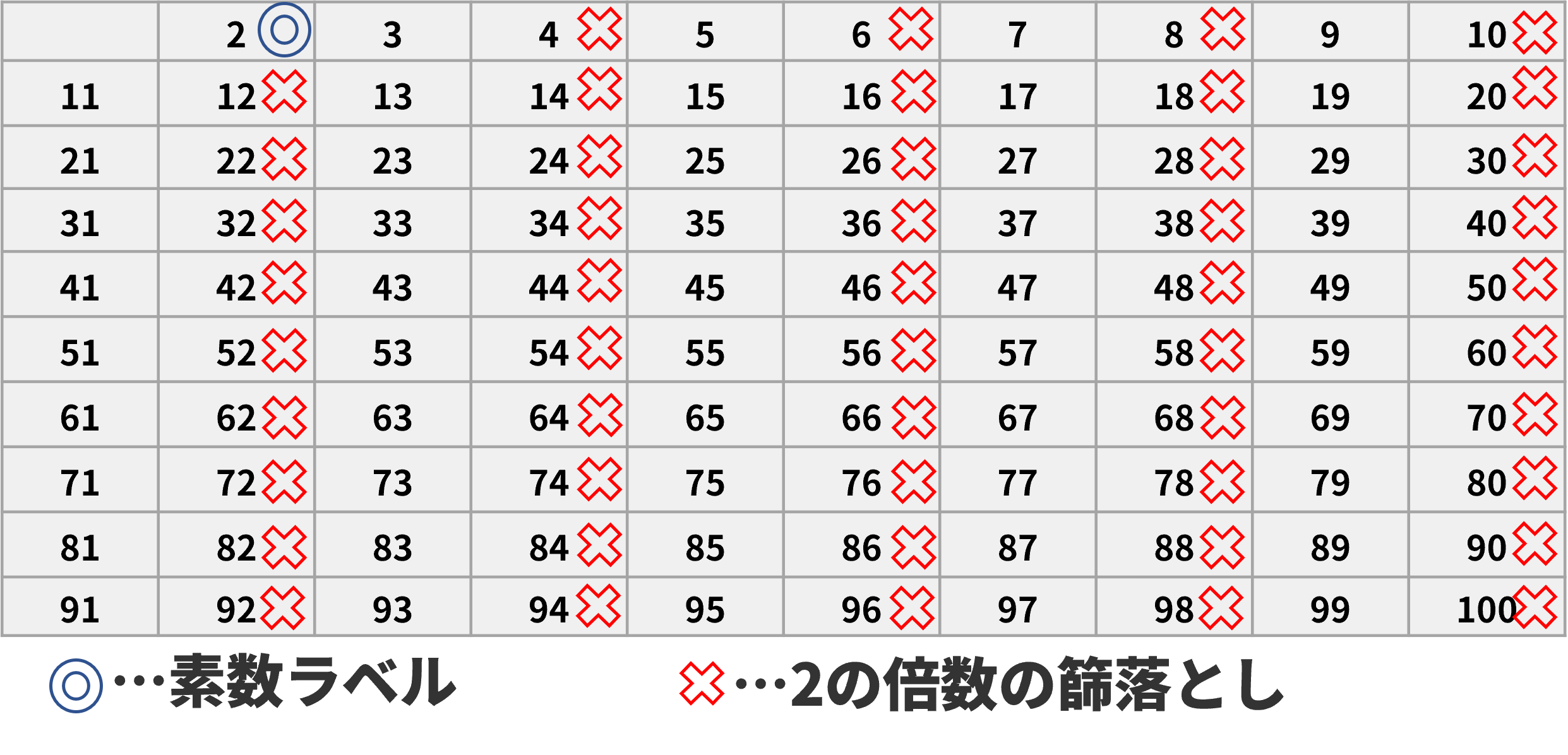
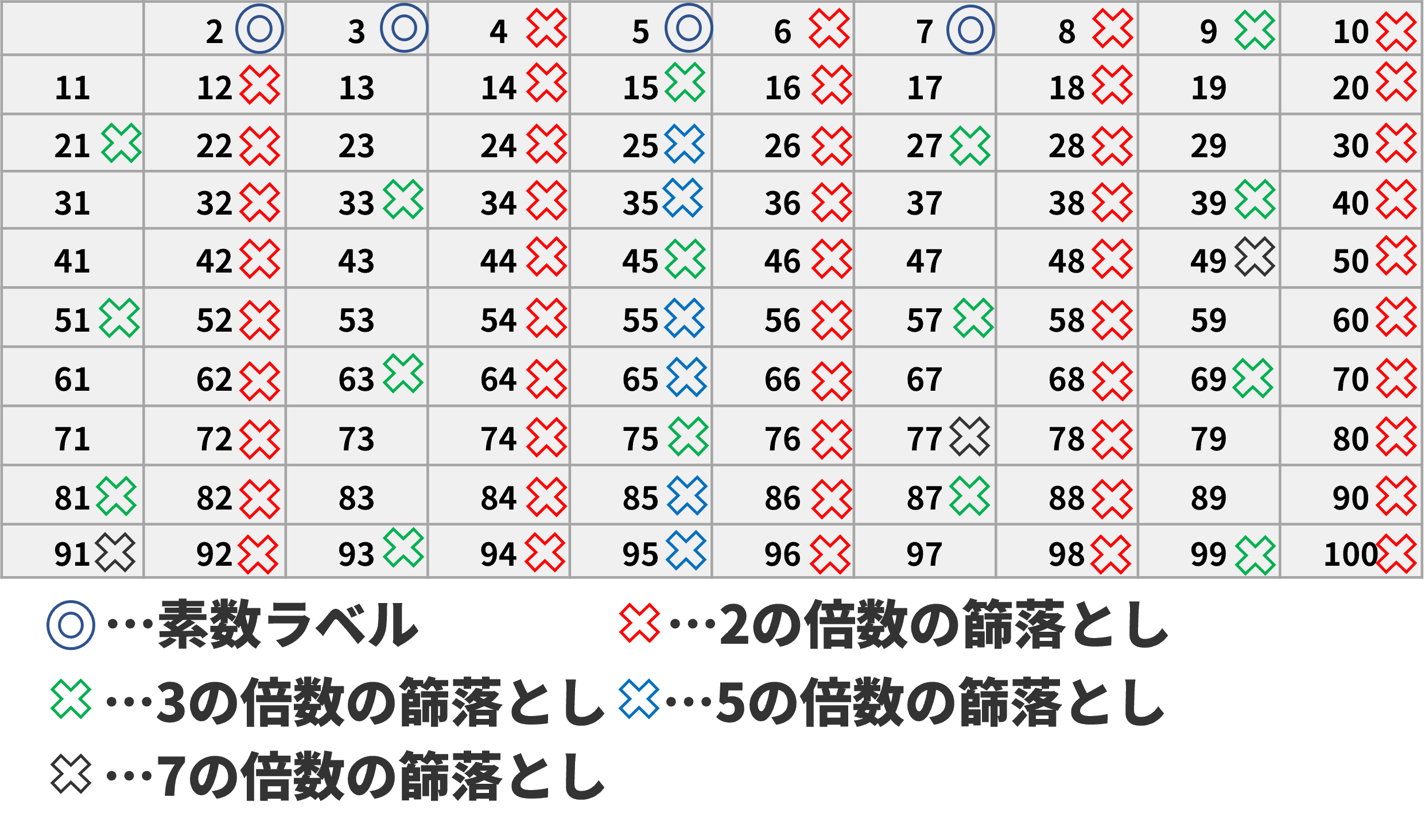
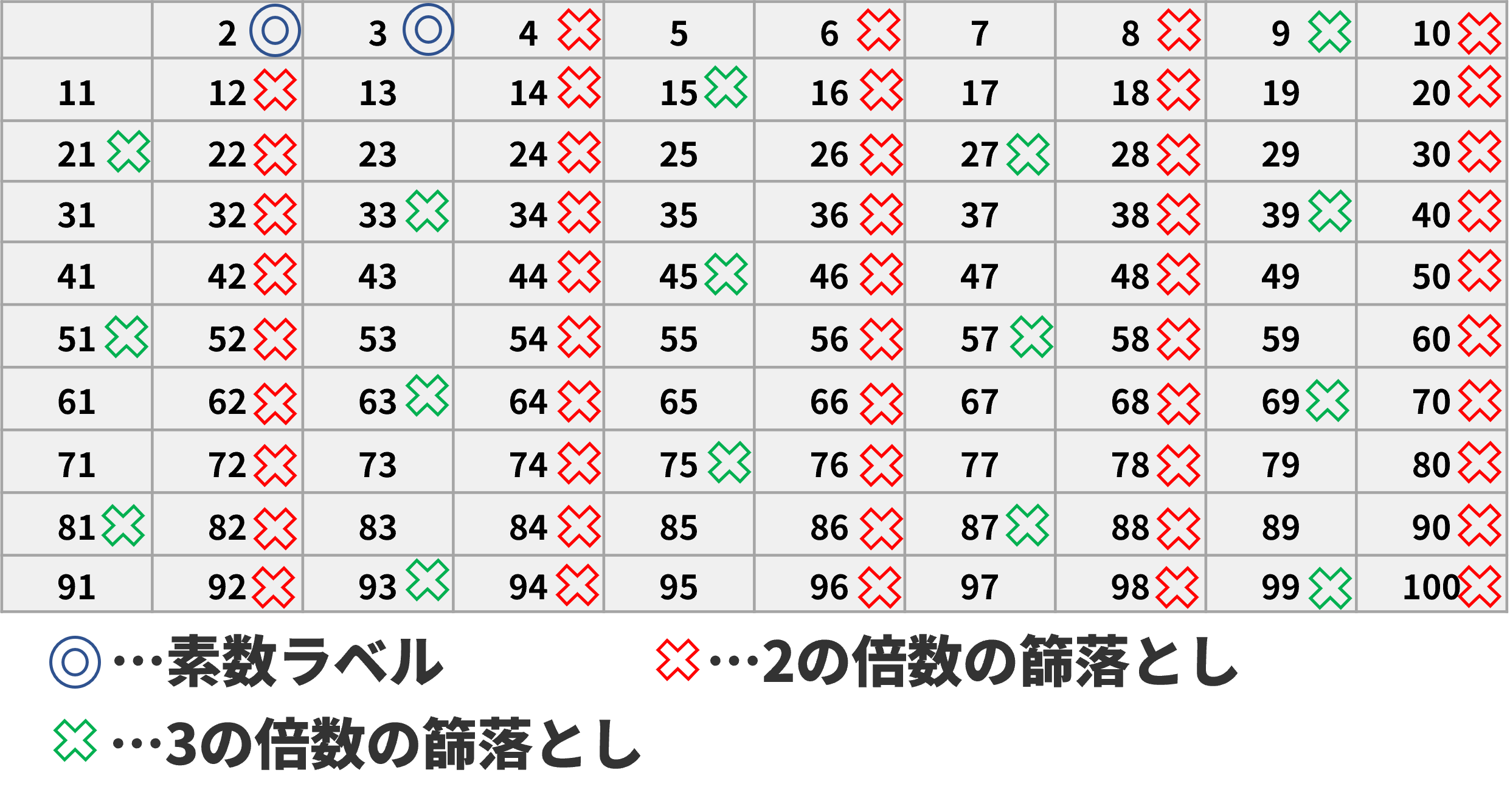
よく知っているじゃないか。では以上たちのルール、理論を踏まえて、素因数分解を早くするにはどうすればいいと思う?

僕は、エラトステネスの篩を使って素数のリストを作り、そのリスト内の数字を使うことで、ただ素因数分解をするより早いと思います。すべての合成数は素数を組み合わせて作られるからです。
(i)の論理があるので、エラトステネスの篩で整数Nまでの素数を割り出し、リスト内に入れれば、Nを構成する素因数はそのリスト内に全部入っていることになります。
いい考えだね。ではその理屈をもとにコードを書いてみようか。

モジュール
既に規定されている専用の部品(処理内容)のこと。プログラミングではそのモジュールを入れるために import を使う。
今回は平方根の仕様を使いたいから、mathモジュールをimportしようか。10行目のように
math.ceil(math.sqrt(n)) とすることでnの平方根を表すことができるよ。



出力結果


~エラトステネスの篩の部分について~
エラトステネスの篩から得たリスト prime を使い判定していく。関数 eratosthenes(N) を定め、まず最初に prime というリストに、 0≦i≦N の範囲内の数をTrue(真)であるとする。次に添字番号0と1、つまりリスト内の0と1の数字をFalseにする。
sqrt(平方根)を使い、変数 sqrt_Nに√Nを代入している。
ちなみに、同じ変数の名前を使う場合、関数内の処理で書けば複数の関数内に分けて使っても大丈夫だよ。でも、関数内で定義した変数を、関数外で表示しようとするとエラーが起きるよ。定義不足になってしまうからね。

(i)のルールより、11行目で i の範囲を2からsqrt_N までの範囲で繰り返す。 if prime[i]: というのは、primeの添字番号 i 番目の数字がTrueである時、という分岐を指す。最初の地点では0と1以外は全て True 扱いになる。2の時、 j の変数が2*i 、つまり2の倍数の2番目である4から N+1 まで、つまり 4≦j≦Nの範囲でi ずつ増やす、つまりi の倍数の数を False にする、ということとなる。そして最終的なリスト prime を戻り値として得る。
この関数のおかげでエラトステネスの篩が定義できるんですね。

〜素因数分解の部分について〜
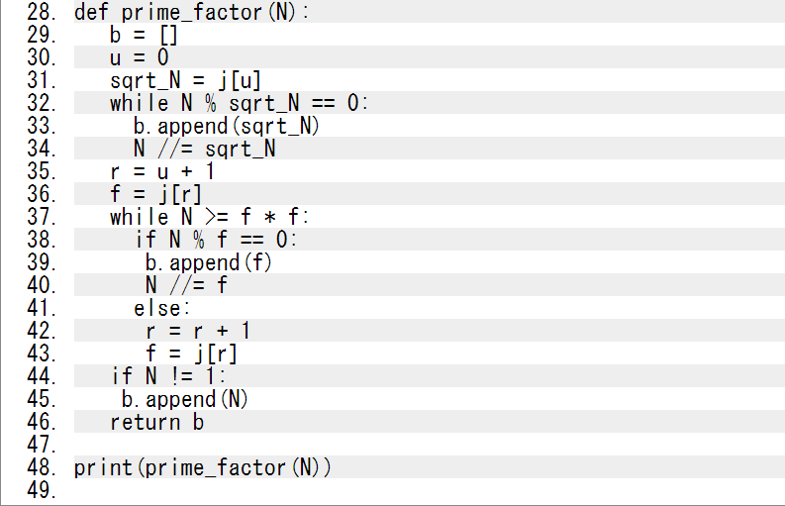
まず、関数 eratosthenes(N) の戻り値を次の関数 prime_factor(N) で使うために、j という変数に空のリストを代入して、そのリストに prime の配列を代入する。これにより次の関数でも使用することができる。
prime_factor(N) の関数内で、最終的にに戻り値として得るためのリスト b を作り、次に u という変数に0を入れる。この変数はリスト j の添字番号を表すためである。
ここで先ほど学んだ while文 と if 文が出てくるんだね。
そう、基本的に組み合わせることであらゆる分岐、条件を表現することができるよ。

この素因数分解のところでは、Nを j[u]で割れるか割れないか、またそれできなかった場合はN自身が素数である、ということを示していますね。
その通りだ。ここで注意することとして、j[u] で割り切れない場合は次の添字番号にする必要があるよね。 u += 1 とすると、実行はできるんだけどどうしても時間が遅くなってしまったんだ。だから別の変数 r = u + 1 とすることで分かりやすくすることが処理時間を短縮することに繋がるよ。

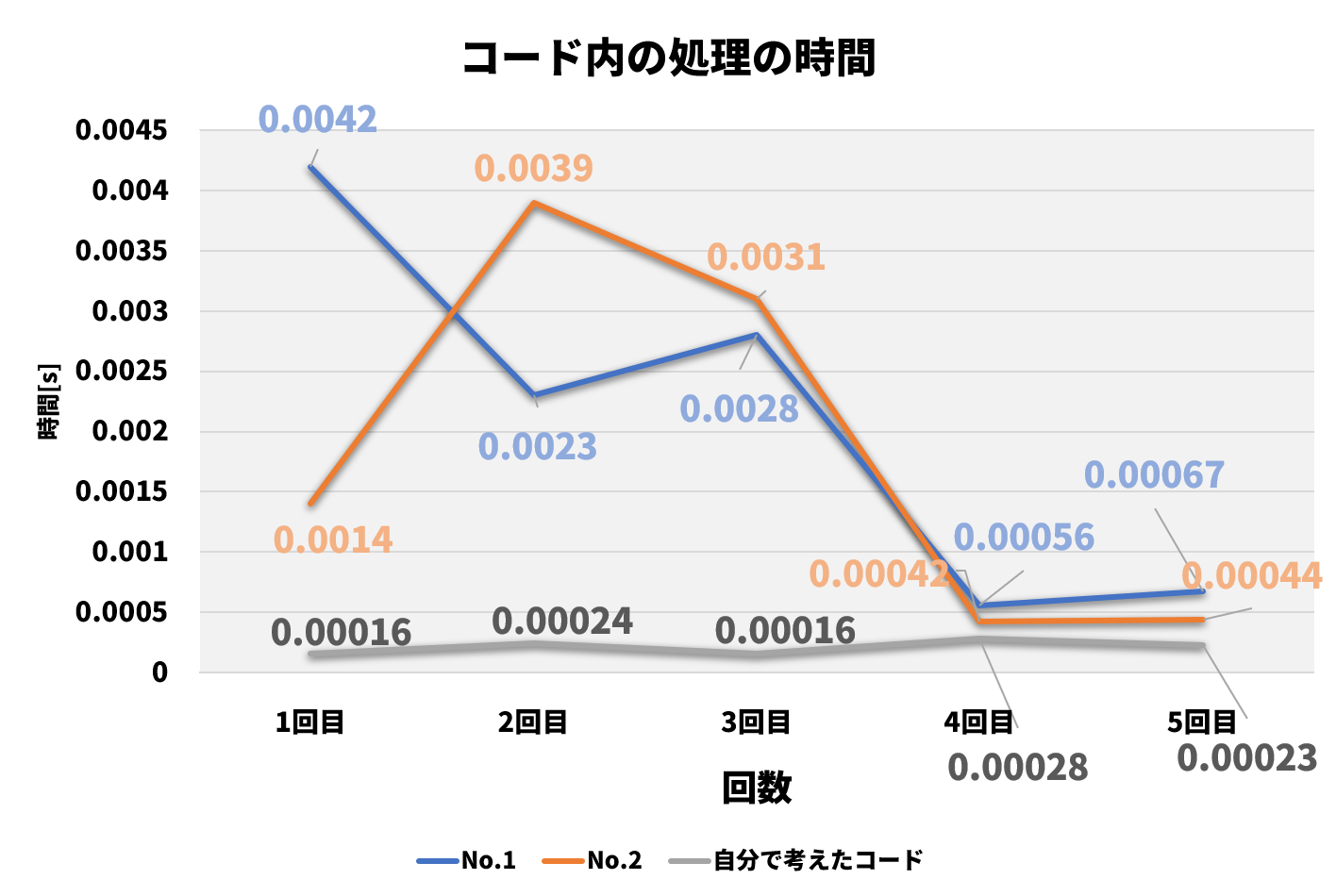
これは?
これはコード内の素因数分解をしたときの処理時間をまとめたものだよ。no.1 と no.2 というものは試し割り方そのものをコードに落とし込んだものだよ。つまり、今回2からNの平方根までのものを2からNまで全てで割っていくというものになるね。時間にムラはあるけど素因数分解の時間は今回作ったものが早くなるね。

なるほど。でもさっきから気になってたんですけど、そんなに時間を気にする必要ってありますか?別に早くても遅くてもいいじゃないですか。
ここで話した処理時間に関しては、次の内容で密接に関わるんだ。だから注目したんだね。


