
公開鍵暗号方式について
話は変わるけど、君たちはネットで情報を第三者に見られないようにする仕組みを知ってるかい?

えー、わかんないよ。どんな仕組みなの。
暗号化
保存されているデータを外部からわからないようにするために全く別のデータに変換する仕組み。
ex) 日本 → N (もし暗号化されたものを復元する場合、Nが日本を指すことを知る必要がある。)
基本的な暗号の仕方には以下の2通りがある。
公開鍵暗号方式
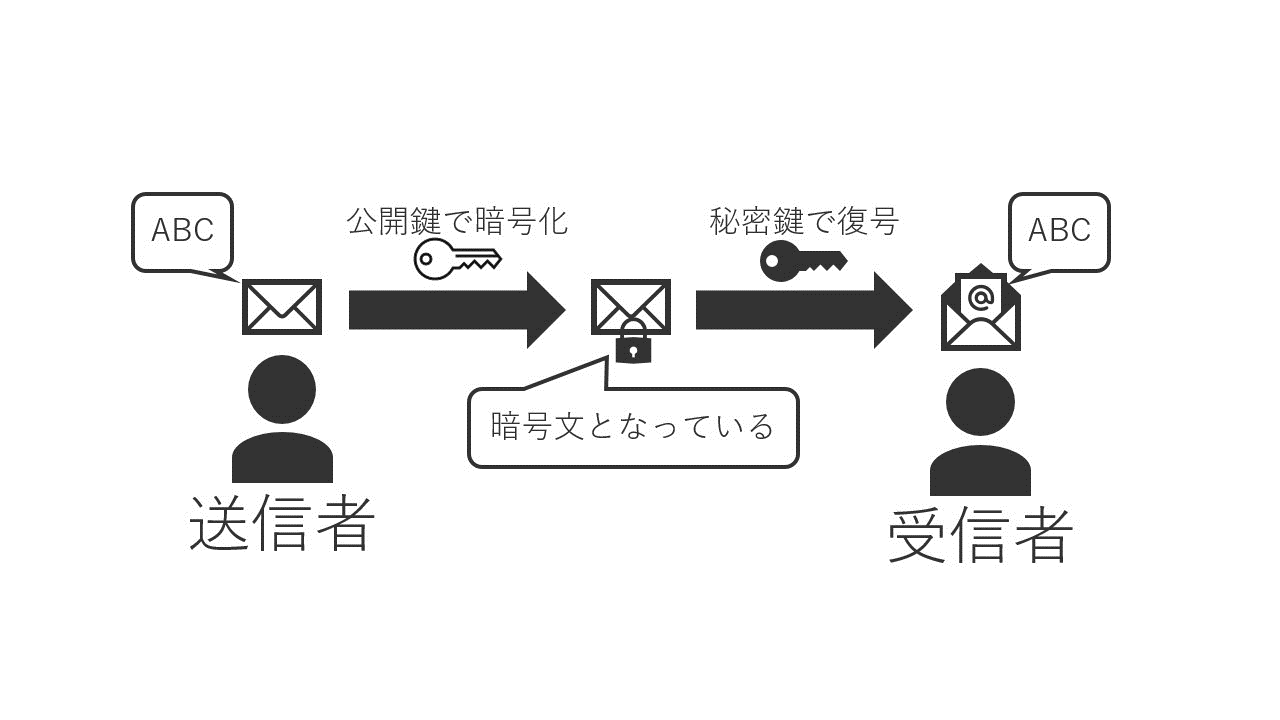
暗号化とその復号時に別個の鍵を使い、暗号化のための鍵を公開できるようにした暗号方式のこと。(送信者が受信側から配られた公開鍵で暗号化し、受信側だけが持つ秘密鍵で復号する。)
共通鍵暗号方式(主にWiFiに使われる)
暗号化とその復号時に同一の鍵を使う暗号方式。その同一の鍵はハジメ定の時間が経つと変更される。
公開鍵暗号方式は安全性が高いですね。
そうだね。その安全性を利用した暗号に RSA暗号 というものがある。

RSA暗号
「素数と素数の積からなる合成数の素因数分解に時間がかかるという性質を安全性の担保としてもつ」ことを用いた最初に実装された '暗号' と 'デジタル署名' の実現が可能で安全な公開鍵暗号方式の1つである。( RSAの由来はロナルド・
リベリスト、アディ・シャミア、レオナルド・エーデルマンという3人の数学者(発明家)たちの名前の頭文字)
ちなみに、RSA暗号 は近年では使われなくなっているんだ。それは技術の進歩によって量子コンピューターというものができたからだね。

その量子コンピューターの前では膨大な数の素因数分解も時間がかからずにできちゃうってことなの?
その通りだ。現在は楕円曲線暗号というものが主流となっているよ。それと君たちは最近のニュースを見たかい。

そういえば、量子暗号通信というものを見かけたような。
それもまた注目されている暗号だね。おっと、話題がそれちゃったね。先ほど言った RSA暗号 はPython で実装できる。仕組みについてさらに知るため一緒にやってみようか。

~RSA暗号~
公開鍵に使いたい要素として、指定した数二つを用意するよ。今回は小さい数で行うけど、実際には膨大な数字を使うからね。さらに、二つの数の最小公倍数を鍵に使いたいんだけど、そこで問題があるんだ。レイさん分かるかい?

それって、結局何の素数と素数をかけたか分かったら、伝えたい情報がすぐに判明するってことかな?
そういうことだね。だから公開鍵は以下のように設定をするよ。

公開鍵の設定:任意の数をp、qとし、Nを(p-1、q-1)の最小公倍数とする。
公開鍵は2からNまでの数の中で、Nと互いに素になる数とする。
互いに素 というものはお互いの数の最大の約数が1である、ということを指しますね。
そうだったね。ちなみに最小公倍数の簡単な求め方ってあるの。
最小公倍数は、2数の最大公約数で2数の積を割ったものだよ。具体例を交えようか。


つまり、互いに素な2数とそうではない2数どちらも 最小公倍数=積 //最大公約数 は成り立つということですね。
そうだね。じゃあその最大公約数を求めるにはどうすると思う?

脳筋で求めてもいいんじゃん、ほら。
ex) 358と587
358=2×179
537=3×179 よって、最大公約数は179
それだと桁数が大きくなった時がきついと思うよ。さらにその例の場合だと、537から358を引くと179になるよね。この数で2数が割れるとすぐわかるから、より脳筋でやると面倒臭いよ。
だから以下のことを用いて最大公約数を求めるよ。

ユークリッド互除法について

去年数学で習ったよね。これが最大公約数を求める方法になるよ。

そういえばやったな。整数のところが絡んでくるんだよね。そしてこの方法をプログラムに落とし込めばいいんだね。
演算子をなんとか駆使すれば表せるね。やってみようか。

今回はmathモジュールを使っていない。仮にモジュールを使ったら最大公約数を求められる関数 gcd() はすでに内包されているが、今回は実際に関数を定義する。
ユークリッドの互除法より、余りが0になるまで処理を繰り返す。
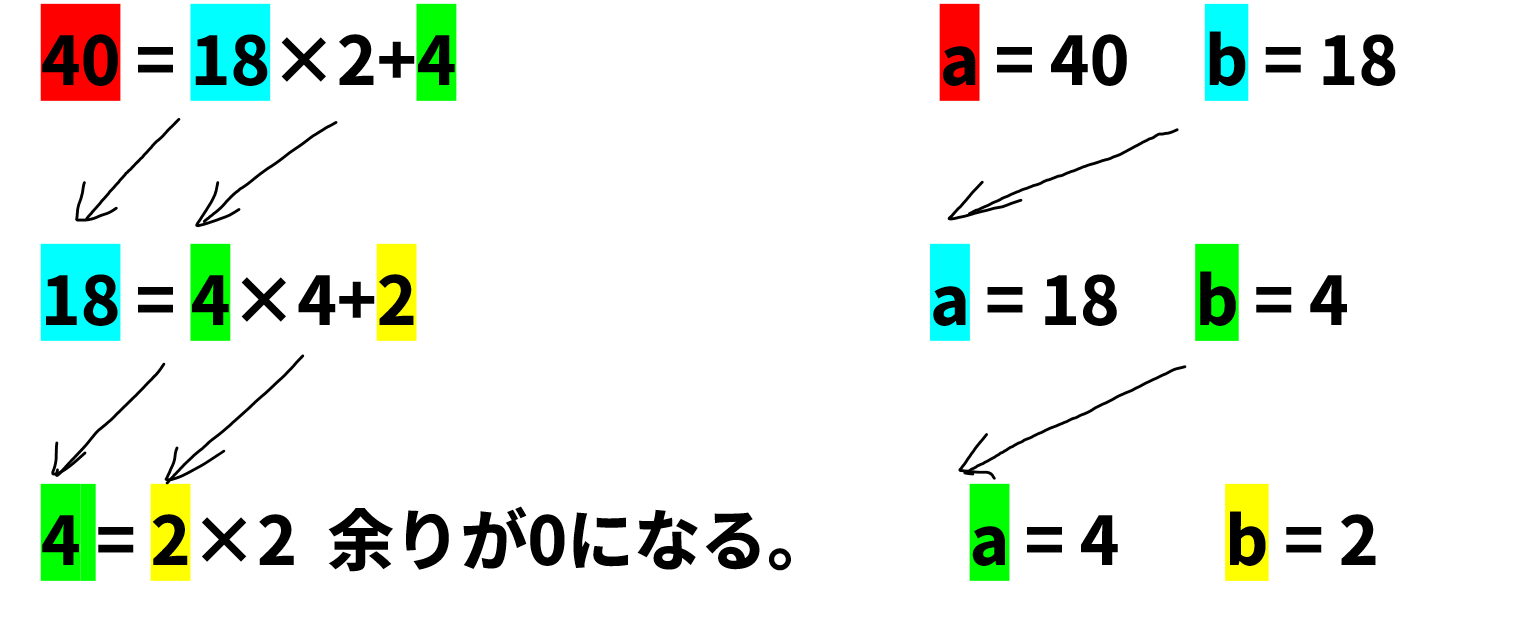
return b より関数の戻り値としてbが得られる。
次に最小公倍数 lcm() を定義する。(mathモジュールに内包はされていない)
関数の戻り値として任意の数 aとb の積を最大公約数 gcd(a,b)で割った数を得る。
そして変数Nに関数を用いてp-1、q-1の最小公倍数を代入している。
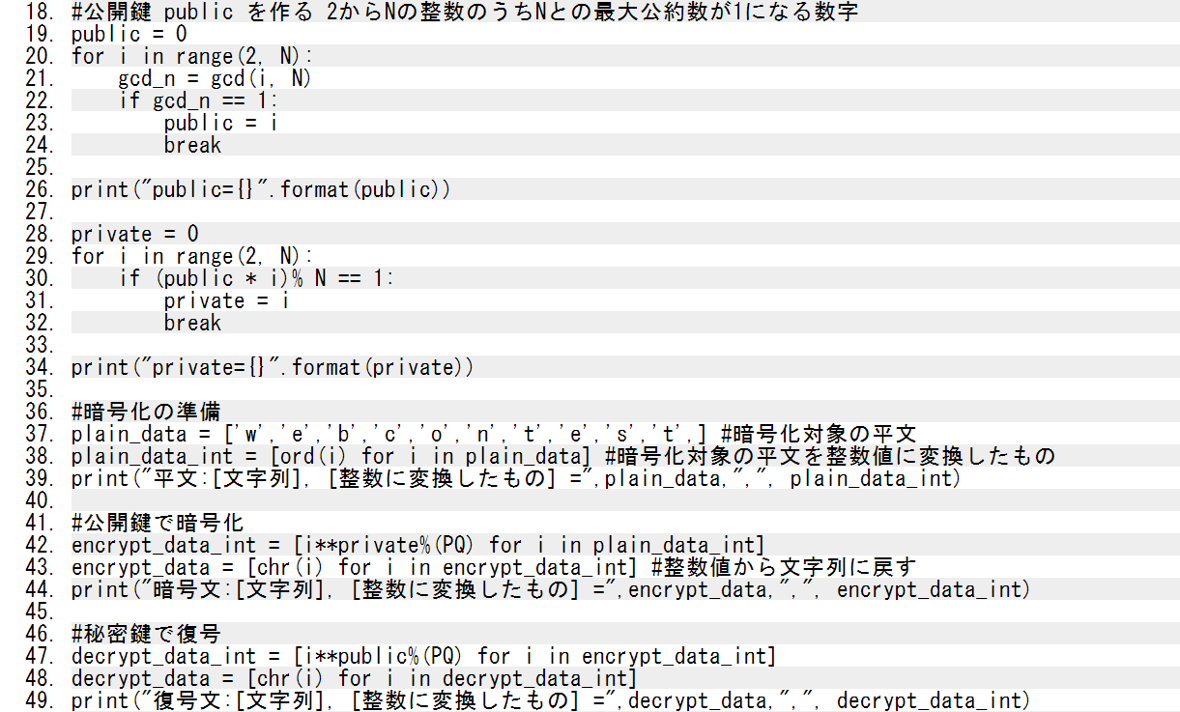
さっきの素因数分解のところでもコードに書いていたけど、長いコードになる時は値を確かめるために print を使うといいよ。これもまたPython がインタプリタ型である利点だね。

format・・・”{}”.format(n) とすることで、{}の中にnを置換する、というものである。 公開鍵 private を作るために 秘密鍵となる変数 public =0で初期化をする。2≦i≦N-1までの中で、i とNが互いに素な数になる時のi を 秘密鍵に設定する。ここではbreakを使っているので、最小の i となっている。また private も初期化する必要がある。 2≦i≦N の中で、public*i を N で割ったときの余りが1の時、そのi をprivate に代入し、公開鍵privateと秘密鍵publicが設定される。
公開鍵の設定に秘密鍵の値を利用する意図はわかるかな?

公開鍵は元となる平文を暗号にし、秘密鍵元に戻すときに使う値なので、その2数を関連づけた値じゃないと、しっかり復号されたかわからなくなってしまうからだと思います。
そうだね。でも実は、平文を暗号化したものを復号することで元に戻せることの説明にはより高度な説明が必要なんだ。やろうと思えばできるんだけどね。

あ、調べてみたら mod とか訳分からないものが出てきたよ。これは何なの?
mod は、プログラミング上でいうなら % だね。割った余りを表せるんだ。

7 =1(mod 2) 2で割った余りを表す。 7(mod 2) = 1 とも表記できる。
あえて復号できる理由を説明するなら、
『互いに素な公開鍵と秘密鍵の値を指数とした数を、共通な整数で割った余りが一致する』かな。深い説明は先生も詳しくは理解できないから、実際そうなると納得してくれたらありがたいよ。

ord関数
与えられた1文字を、Unicode値に変換する関数。Unicode とは、文字を表す数字のことである。
chr関数
与えられた数字を、Unicode 文字に変換する関数。ord関数の逆を指す。

出力結果
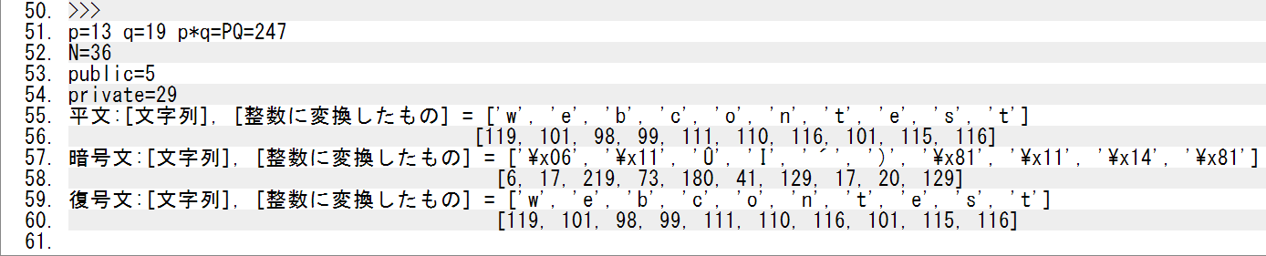
さて、これまで多くのことを学んできたけど、レイさんはプログラミングに対しての見方はどうなったかな、レイさん。

やってて思ったのが、確かに流れを抑えて段々と理解できることがとても良かったな。今後もプログラミングについて学びたいと感じるきっかけになれたよ。ありがとうございました。
僕も改めて基礎について覚えられて、また発展的な内容にも触れることができてよかったです。ありがとうございました。
そういってもらえると嬉しいよ。


