ゲームを少し変えてみた
先ほど紹介したゲームは我々の先輩が発見したもので、Mathematical Gazetteを初めとして、いくつかの数学雑誌に掲載されました。我々は「ゲームのルールを少しずつ変化させていっても、この性質は現れるのか?」と考え、研究しました。ここからは我々の研究によってさらに発見したゲームを紹介します。ここからあとの内容は、私達が国際学会Japan Conference on Discrete and Computational Geomery, Graphs and Games 2017の論文査読を通過して発表した内容です。
ゲーム①:p人のプレイヤーが順番に箱からカードを交互にs枚ずつ取り出し,初めて赤のカードを引いたプレイヤーが負けるゲーム
このゲームにおいて変更した点はプレイヤーが引くカードの枚数です。従来は各プレイヤーが1枚だけ引くというルールでしたが、ここではカードを引く枚数を任意に選択します。例えば、s=3と設定すれば各プレイヤーは「カードを3枚ずつ引く」という様にルールが変わります。
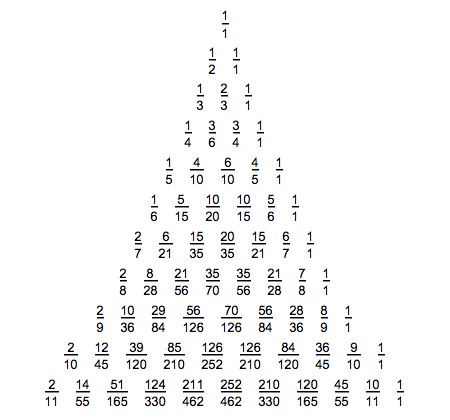
このゲームにおいてもパスカル的三角形の性質を生み出すことが分かります。例えば下図はp=3,s=3とし、最初のプレイヤーが負ける確率を三角形状に並べたものです。見ての通り、どこをとってもパスカル的三角形の性質が成り立っていることがわかります。

これにより、基本的にカードを引く枚数を複数にしてもパスカル的三角形の性質が成り立つことが分かりました。
ここからさらに応用して各プレイヤーごとにカードを引く枚数を設定できるというルールにします。
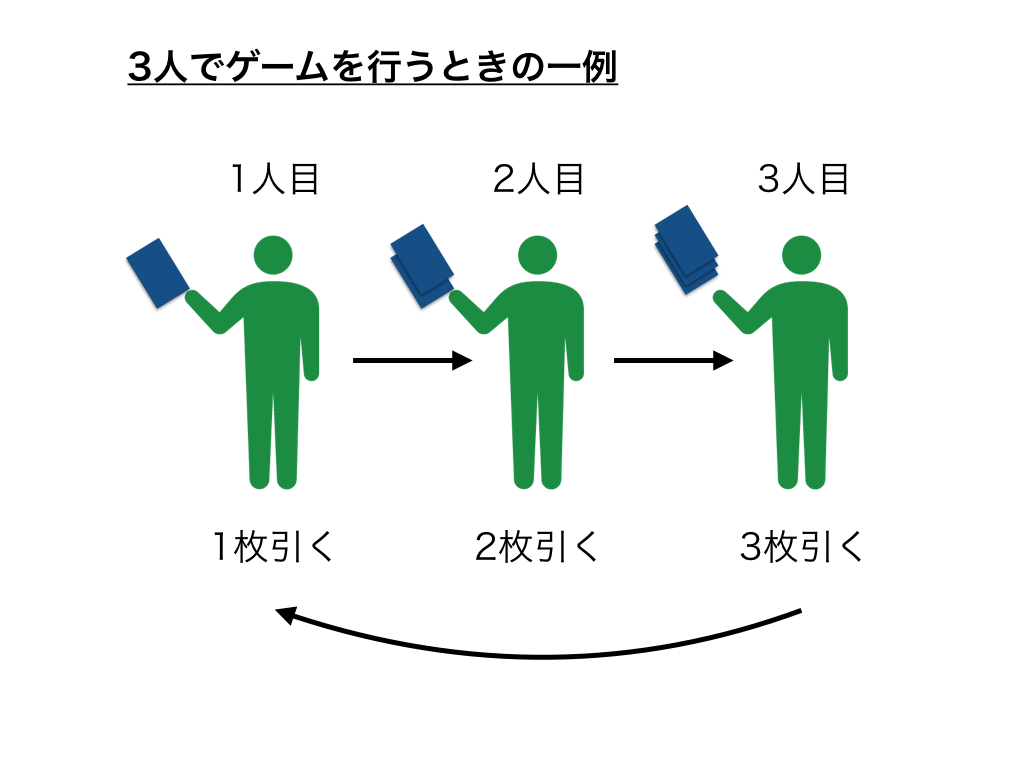
具体的な一例を挙げて説明します。3人でゲームを行い、1人目のプレイヤーは1枚、2人目は2枚、3人目は3枚ずつ自分の番に引きます。この場合においてもパスカル的三角形の性質が成り立ちます。(図は最初のプレイヤーが負ける確率を参照しています)
ここまでのまとめは定理として次のようになります。証明は添付論文にあります。
p人のプレイヤーがそれぞれs1,s2...sp枚ずつカードを引き、初めて赤のカードを引いたプレイヤーが負けるゲームにおいて、特定のプレイヤーが負ける確率を三角形に並べると、パスカル的三角形となる。ただし、勝負が決まらない場合を省く。
ここで勝負が決まらないことが起きるのは、カードの枚数が少なくて、誰も負けることがないままにカードを使ってしまう場合である。
pやsにはそれぞれ任意の自然数が入り、それがいかなる性質においてもパスカル的三角形の性質が成り立ちます。このように変数等を用いて物事を抽象的にすることを「一般化」といいます。
pとs、そしてvの値を決めて、パスカル的三角形を作ってみましょう。vとは、負けるプレイヤーが何番手であるかを表しています。パスカルの三角形のような性質が成り立ちます。
ゲーム②:2人のプレイヤーが箱からカードを交互にs枚ずつ取り出し,赤のカードが出たらためておき、集まった赤のカードがg枚になったプレイヤーが負けるゲーム
これまでは赤のカードを1枚でも引くと負けというルールでしたが、今回はそこを一般化します。今まで赤のカードを1枚でも引いてしまった時点で、勝敗が決定していました。そこで負けとなる赤のカードの枚数を設定できるように変更しました。例えば、g=3と設定すればプレイヤーは赤のカードを3枚集めたときに負けとなります。なおプレイヤーの人数は2人で固定します。
このゲームにおいてもパスカル的三角形の性質は成り立ちます。(ただし、その性質が成り立つのは下図の赤線で囲った部分です。)
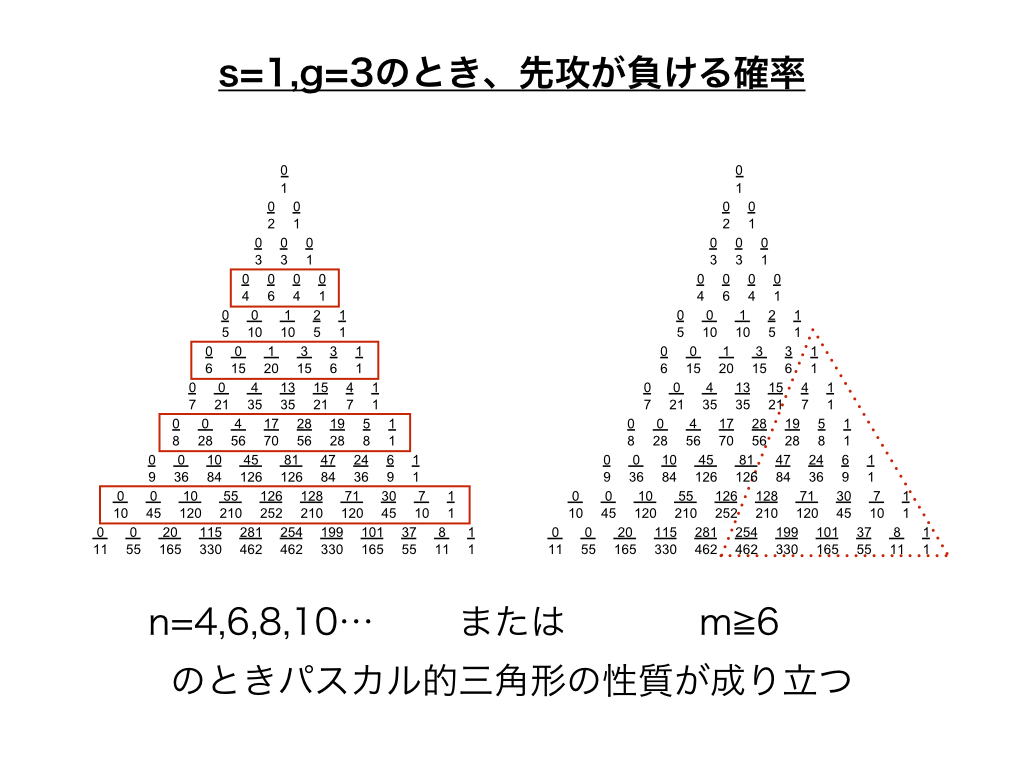
さらに応用し、gの値をそれぞれプレイヤー別で設定した場合を見ていきます。例として、先攻が2枚ずつカードを引き、2枚集めたら負け、後攻が3枚ずつ引き、3枚集めたら負けというルールでゲームを行います。
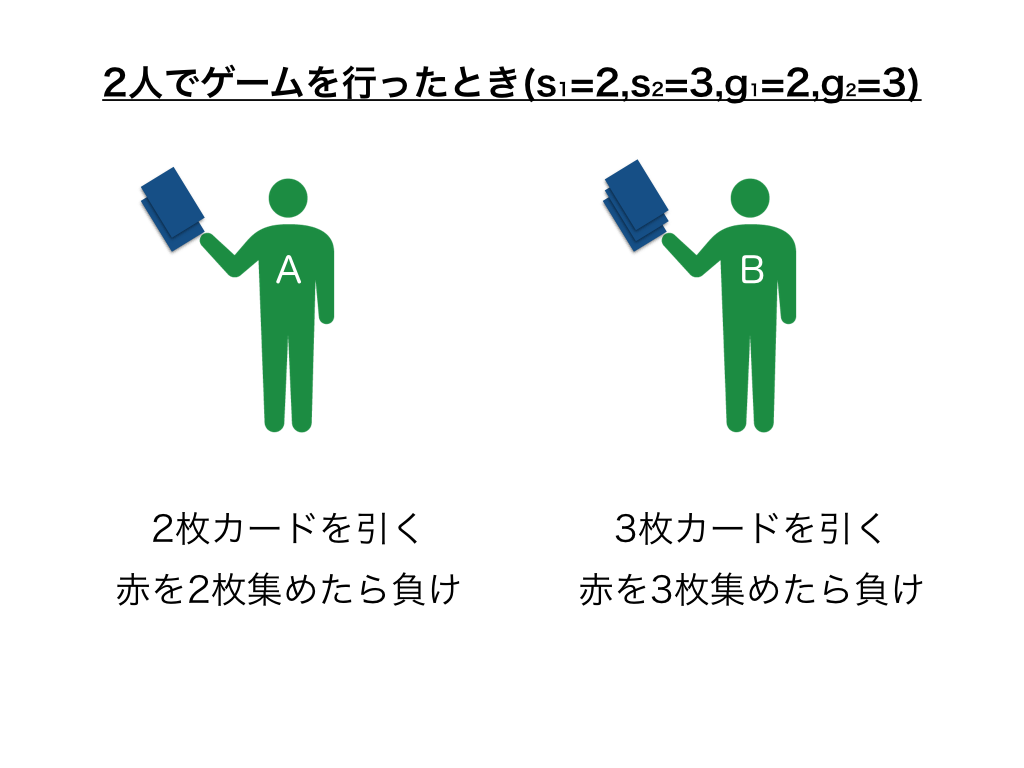
この場合でもパスカル的三角形の性質が成り立ちます。(ただし、その性質が成り立つのは下図の赤線で囲った部分です。)
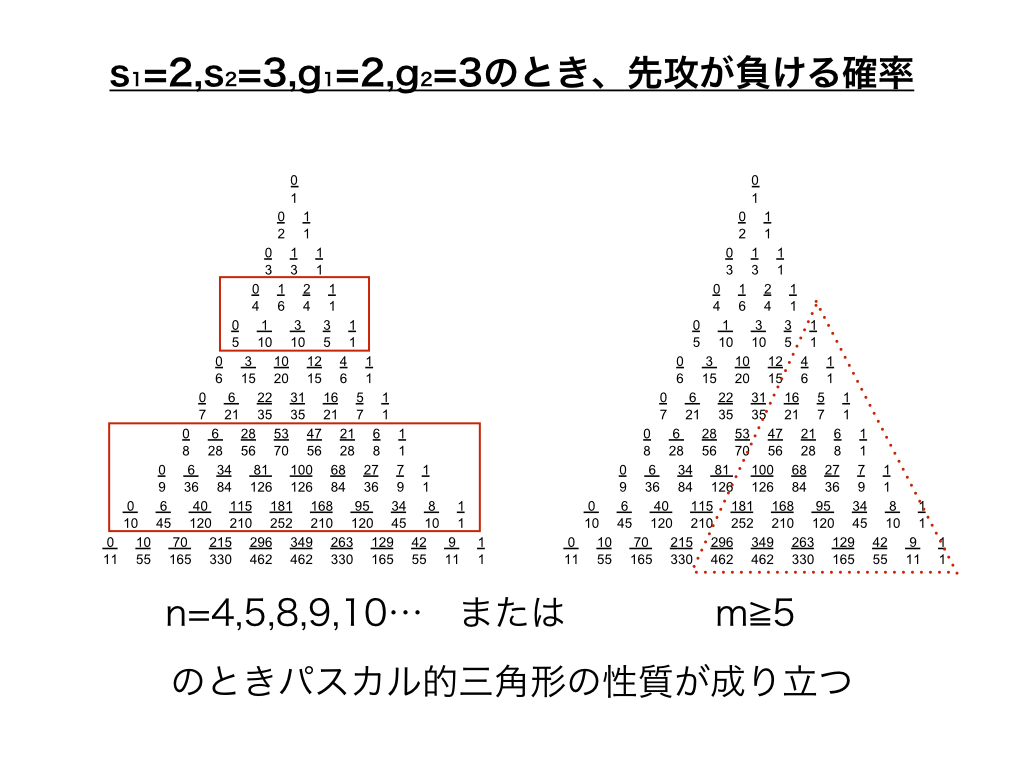
ここまでのまとめ
2人のプレイヤーがそれぞれs1,s2枚ずつカードを引き、赤のカードをそれぞれg1,g2枚集めたとき負けるゲームにおいて、パスカル的三角形の性質が成り立つ。なお、勝負が決まらない場合を省く。
s1,s2,g1,g2の値を決めて、パスカル的三角形を作ってください。パスカルの三角形的な性質が成り立つところと、そうでないところがあります。
このように少しゲームのルールを変えてみてもパスカル的三角形の性質が現れるパターンは多く存在することが分かりました。
