3種類のカードを用いたゲーム
これまで紹介したゲームで用いた赤、白のカードに加えて、新しく青色のカードを追加してゲームを行います。この時青のカードを「赤のカード2枚分」というルールをつけて、上記のルールでゲームを行った場合でもパスカル的三角形の性質を持つことがわかりました。
「箱の中にカードが入っており、うち1点の赤のカードがp枚、2点の青のカードがq枚、0点の白のカードがr枚である。その箱の中からAとBの2人のプレイヤーがカードを2枚ずつ引いていく。Aはカードを1点集めたら負け、Bは2点集めたら負けとなる。」というルールのゲームを例にして見ていきます。
このゲームにおいてAの負ける組み合わせの数を関数U(p, q, r)で表します。そしてUを下の図のように並べます。
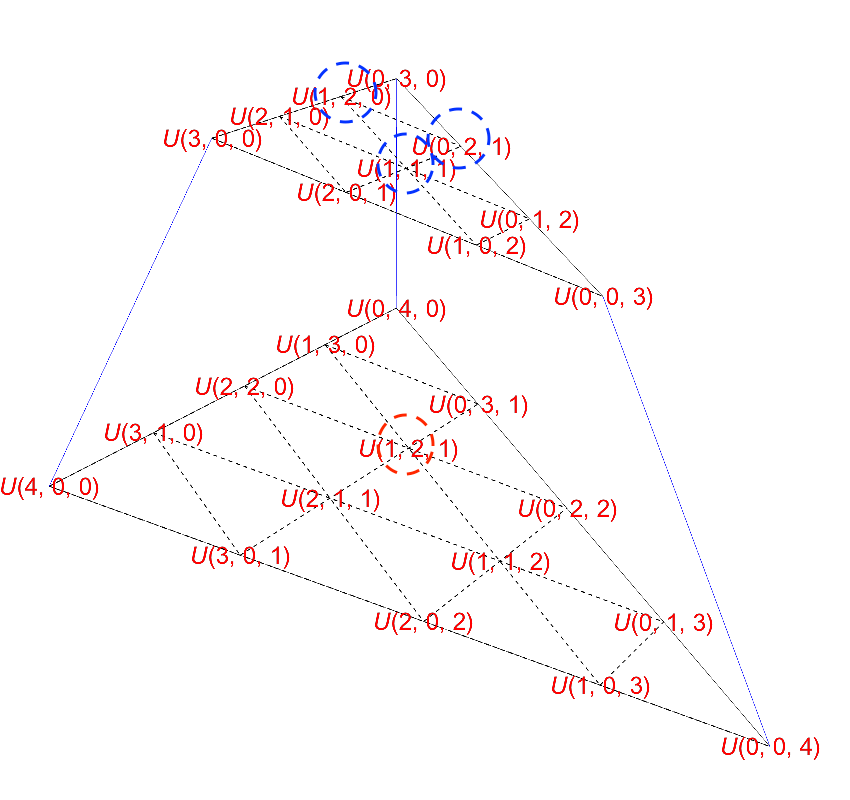
この立体は青丸の和が赤丸になるというパスカル的三角形の性質があります。
これを実数で表すと次のようになります。
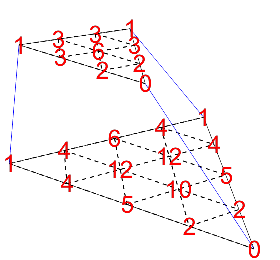
よりイメージしやすいように2次元の2つの三角形に分けました。下の図でも青丸の和が赤丸の和となっています。
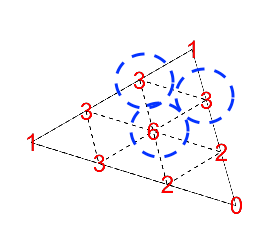
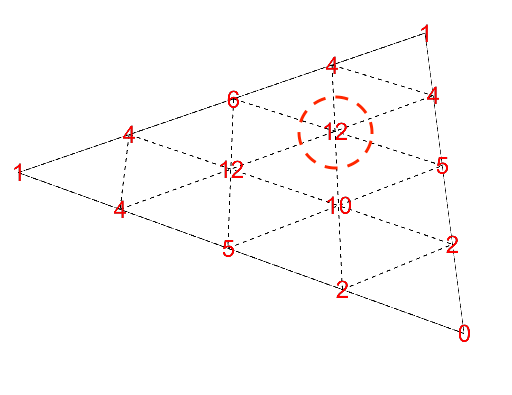
どの箇所を見てもパスカル的三角形の性質が成り立つことがわかります。
