パスカルの三角形の性質
パスカルの三角形には色々な性質を持っています。本ページではその中からいくつかを紹介します。
パスカルの三角形の作り方
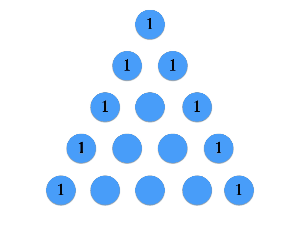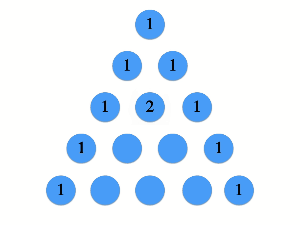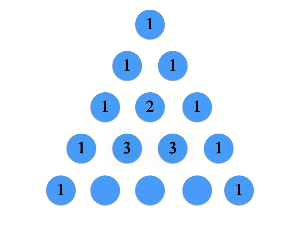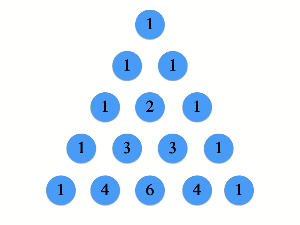
パスカルの三角形の作り方は非常に単純なルールに基づいています。
まず1段目と各段の両端に1を置きます。そしてその他の数は左上と右上の数の和を置きます。例えば3段目の2番目の数は1+1=2です。また、5段目の3番目の数は3+3=6です。
二項定理との関係
二項定理は(a+b)nの展開を記述したもので、これを展開したときに現れる係数を二項係数といいます。パスカルの三角形には構成要素の中に二項係数が現れるという性質があります。

例えばn=2のときの展開式の係数は1,2,1、n=3のときの展開式の係数は1,3,3,1です。これらはそれぞれパスカルの三角形の第3段、第4段と一致します。
組み合わせとの関係
組み合わせは基本的にnCmという形で表され、n個の中からm個を取り出す場合の数を示します。
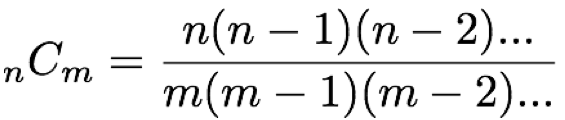
例:箱の中の6枚のカードの中から2枚を引く組み合わせ
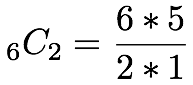
なのでこの答えは15通りとなります。
この組み合わせを図のように並べることで、パスカルの三角形を作ることが出来るのです。
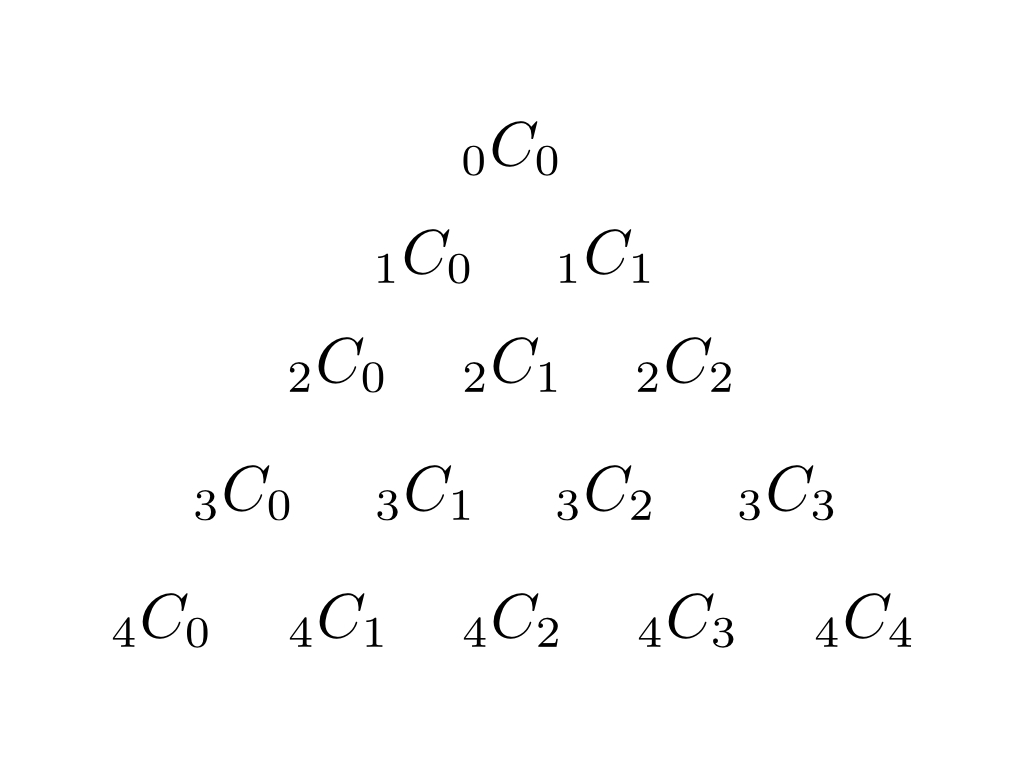

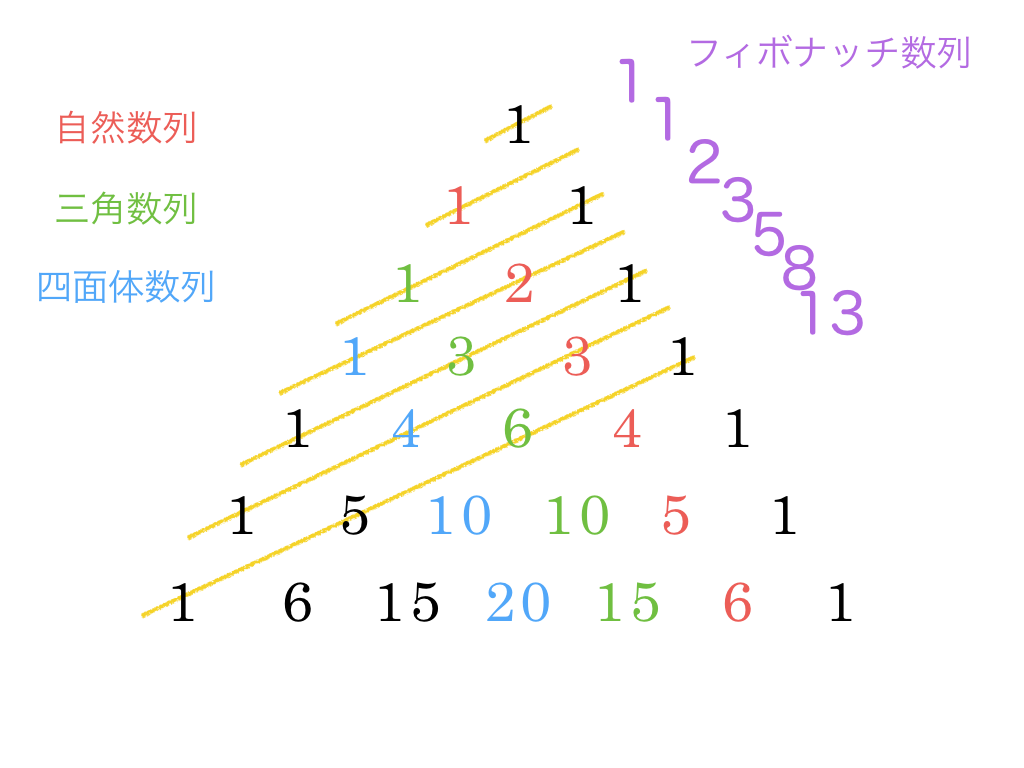
パスカルの三角形と様々な数列
このパスカルの三角形を調べると様々な種類の数列が隠れていることがわかります。
①まずは各段の右端(右から1番目)の数を見てみます。
1,1,1,1,1...と全て1が並んでいることがわかります。ここから1つずつ左に注目する数をずらしていきます。
②各段の右から2番目の数を見ると
1,2,3,4,5,6...と並んでいて、これらは自然数(正の整数)の順に並んでいることがわかります。
③次に各段の右から3番目の数は
1,3,6,10,15,21...で三角数(点を正三角形状に並べたときの点の総数)が並んでいるものです。
④各段の右から4番目の数は
1,4,10,20...で四面体数(点を正四面体状に並べたときの点の総数)が並んでいるものです。
また、パスカルの三角形に斜めに線をとり、その線上の数の和を並べると
1,1,2,3,5,8,13,21...という数列が現れます。
これはフィボナッチ数列といい、隣り合った2項の和が次の項の数になっているというものです。例えば、数列の4番目の数である3は直前の2数1,2の和です。また、5番目の数である5は2,3の和です。
パスカルの三角形が作るフラクタル図形
フラクタル図形とは「どれだけ拡大しても複雑な構造をとる図形」のことです。パスカルの三角形もこのフラクタル図形を持っています。
パスカルの三角形において、2で割った余りが0、つまり偶数を青、余りが1、つまり奇数を紫に色分けしていくと美しい規則性が現れます。これもフラクタル図形のひとつです。

また、3で割った余りでもフラクタル図形が現れます。図では2で割った場合に加えて余りが2の数は赤色で示しています。
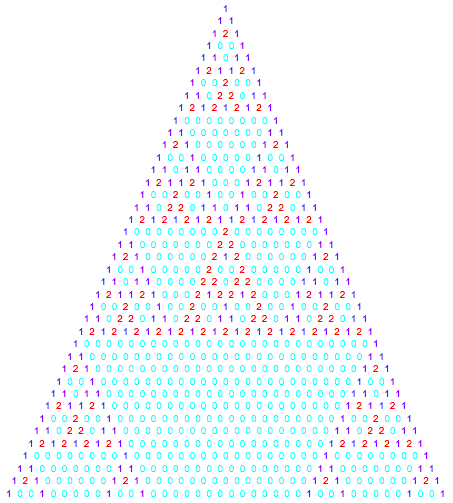
3次元のパスカルの三角形
パスカルの三角形は3次元に拡張することができます。3次元のパスカルの三角形は三項定理との大きな関わりがあります。
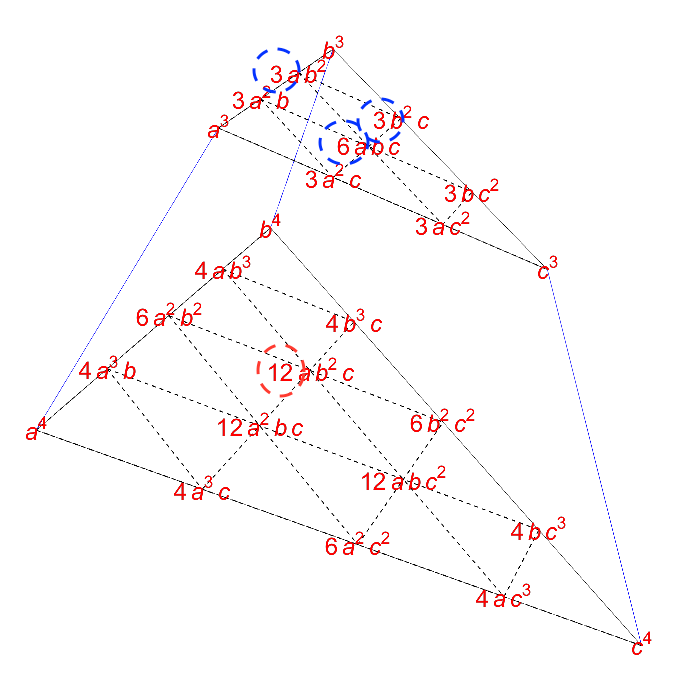
図の赤丸の係数は、上の青丸の係数の和となっています。なぜこのような性質が現れるのかを説明します。
図の立体を2つの三角形に分けて考えます。この2つの三角形はそれぞれ(a+b+c)3と(a+b+c)4を展開した項を三角形状に並べたものになっています。(a+b+c)3や(a+b+c)4のような(a+b+c)nの展開を記述したものを三項定理といいます。この2つの三角形が関係した性質についてお話しします。
^3.png)
^4.png)
(a+b+c)4の三角形の12ab2cを例に説明します。(a+b+c)3の三角形において、(a+b+c)4の三角形の12ab2cと同じ位置にあたるのは6abcです。また、6abcの上に位置するのは3ab2、3b2cです。それぞれの項の文字だけをみると、(a+b+c)3の三角形のabc,ab2,b2cは(a+b+c)4の三角形のab2cをそれぞれb,c,aで割ったものになっています。また、係数をみると、(a+b+c)3の三角形の6,3,3の和は、(a+b+c)4の三角形の12と等しいです。
これらの性質はどの箇所においても成り立ちます。
