In the sample questions for the "Information" published on November 9, programming was mentioned in the third question. Taking this into consideration, I decided that learning programming in "Information" using the textbook would not allow me to understand the details, so I looked into prime numbers. The reason for this is that prime numbers are deeply involved in the network aspect of modern encryption. A typical example of encryption is the RSA cipher.
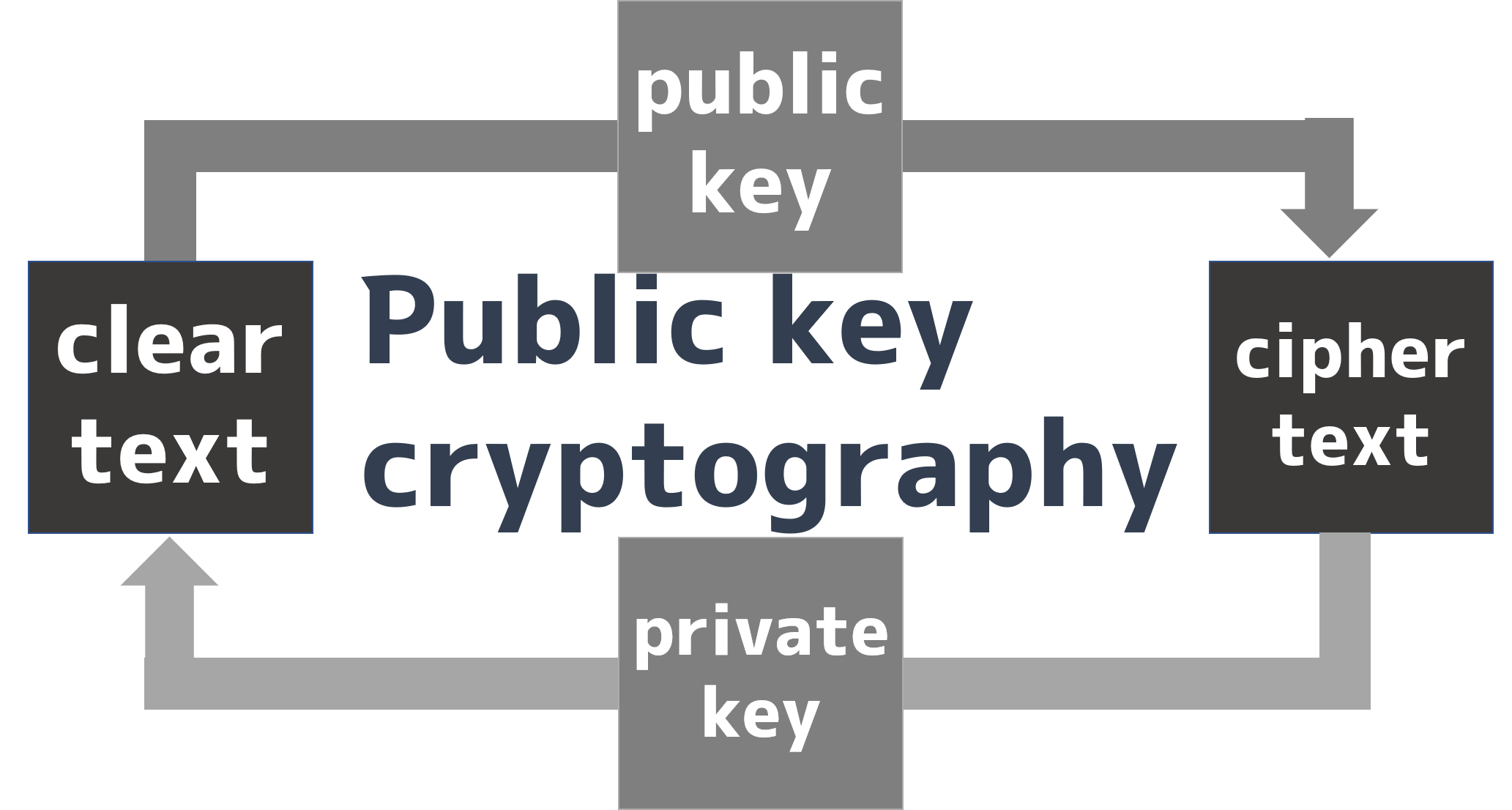
A prime number is any number N that is divisible only by 1 and N itself. The RSA cipher is one of the first public-key cryptography schemes that can realize "cryptography" and "digital signatures" by "using as security guarantee the property that the prime factorization of a composite number consisting of a product of prime numbers takes time."First, the RSA cipher, for example, "15" the product of a prime number and a two-digit number, can be easily computed as 3×5. When the product is 221, a three-digit prime number, it is calculated as 13×17, which takes time. And when the product is 3763(53×71), which is four digits, it takes more time than when it is three digits.This shows that the more digits there are, the longer it takes the computer to decipher them. Next, a public-key cryptosystem is, for example, "If a padlock is used as a key, an open padlock is used as the public key, and the key that can open this padlock is the private key." The receiver delivers the opened padlock (the public key), and the sender locks the key by itself and sends it to the receiver. The recipient can decrypt the lock by unlocking it with its own private key. (Incidentally, RSA comes from the first letters of the names of three mathematicians (inventors), Ronald Liberstein, Adi Shamir, and Leonard Edelman.) In this section, we will deepen our understanding of prime numbers through programming.

※　The codes listed on the following pages follow the textual description.