In the trial division of No. 1 and No. 2, prime factorization has been used to find out prime numbers, and the sieve of Eratosthenes is used simply to find out what numbers are prime.
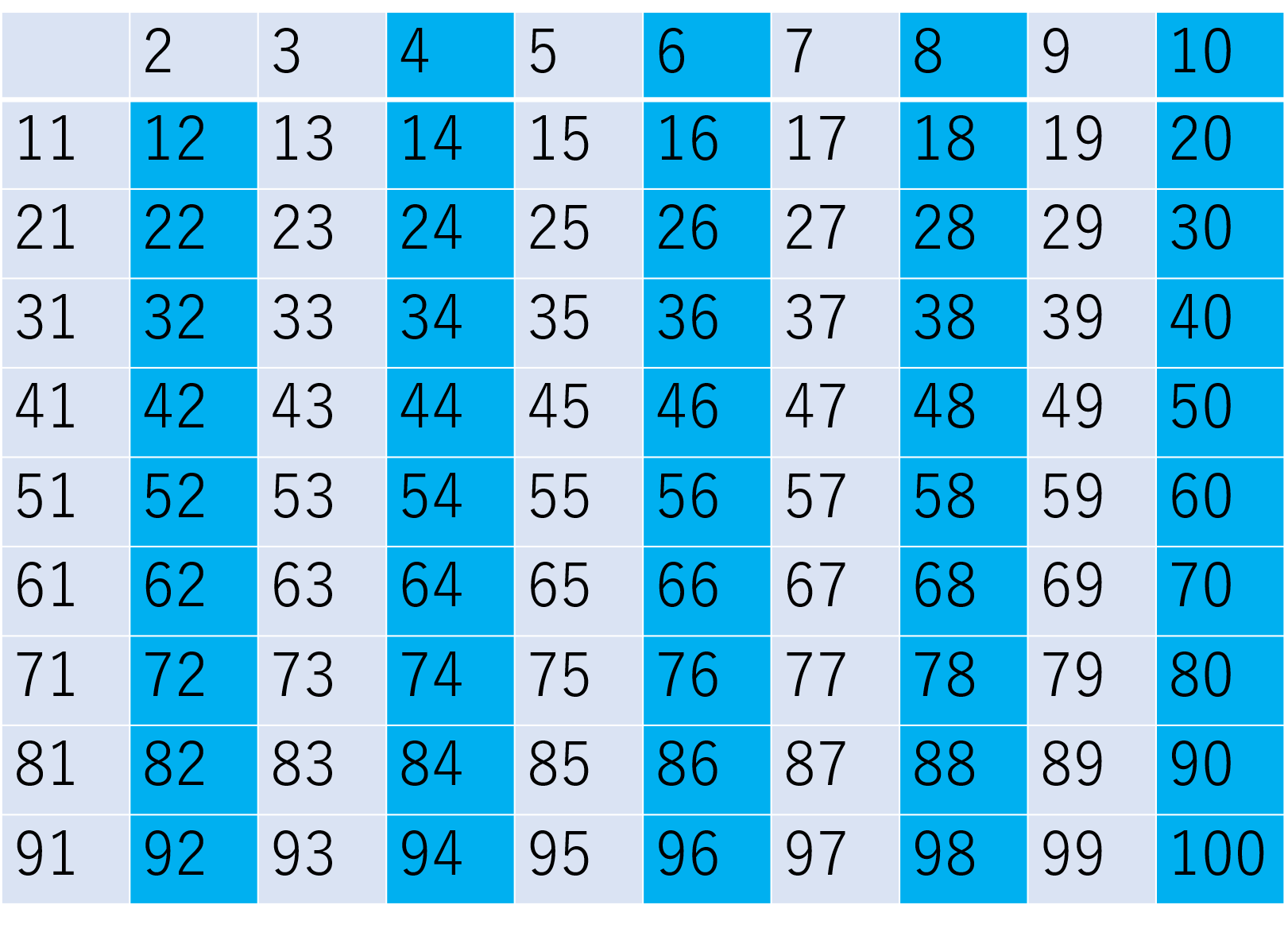
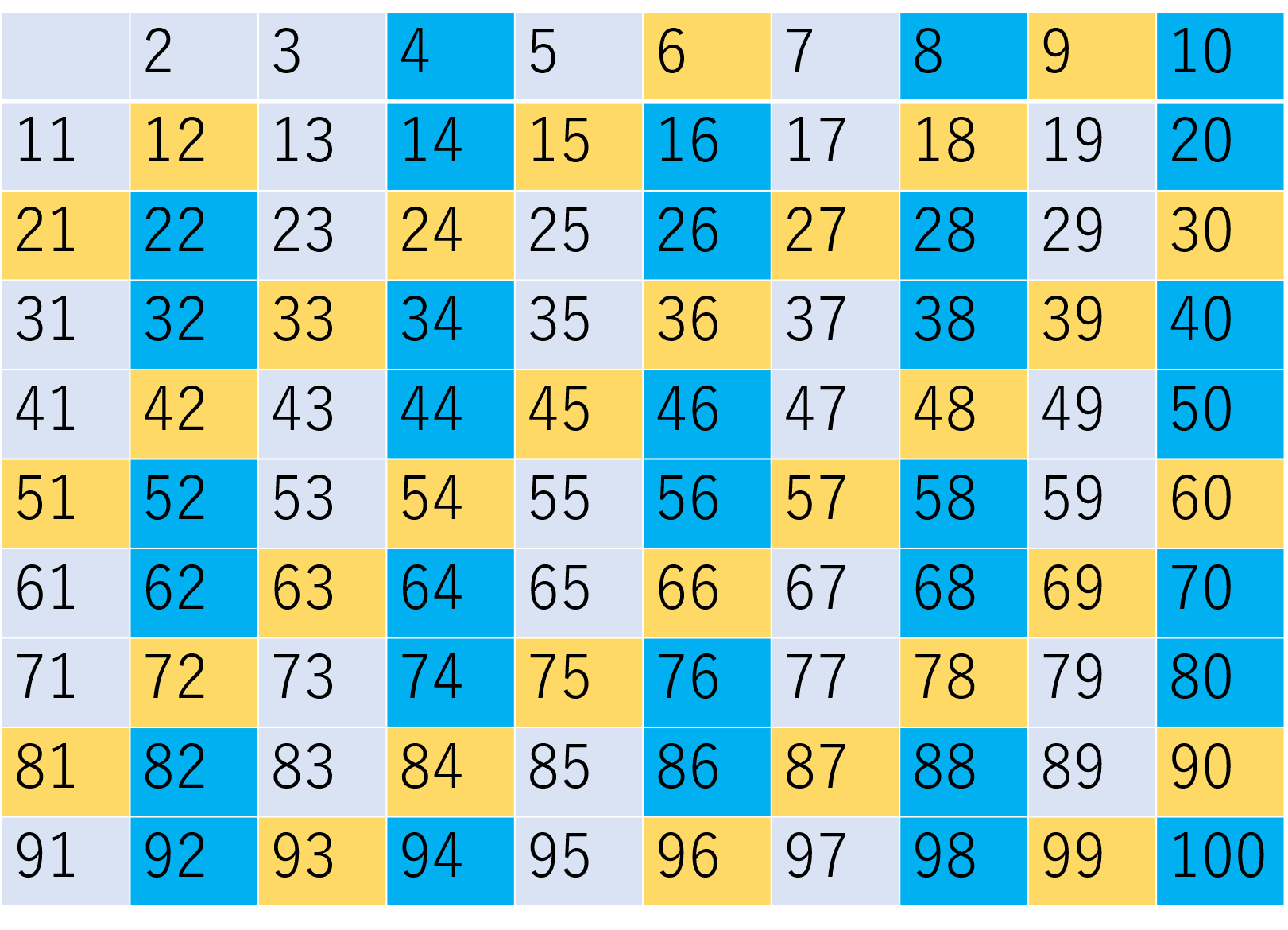
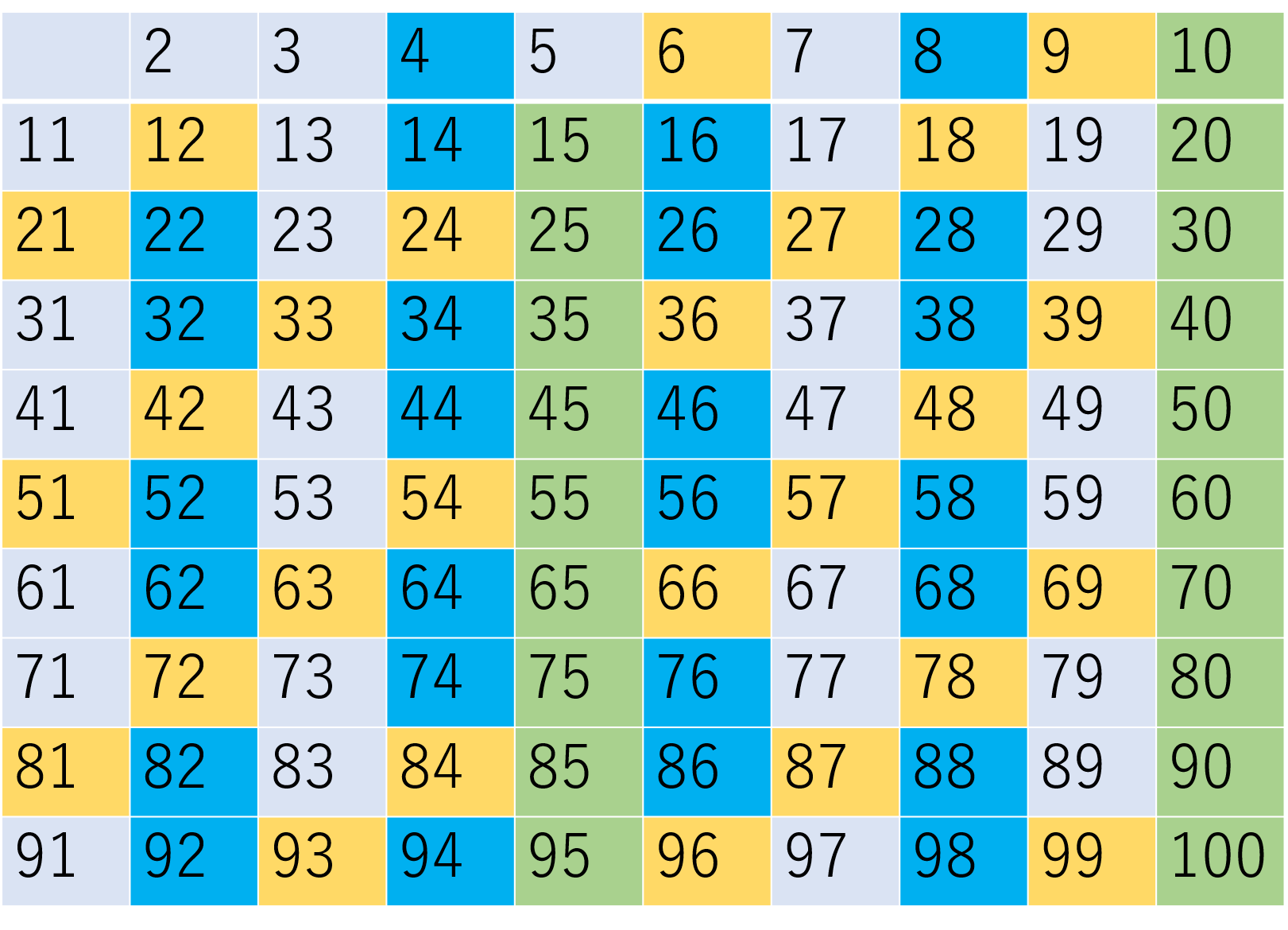
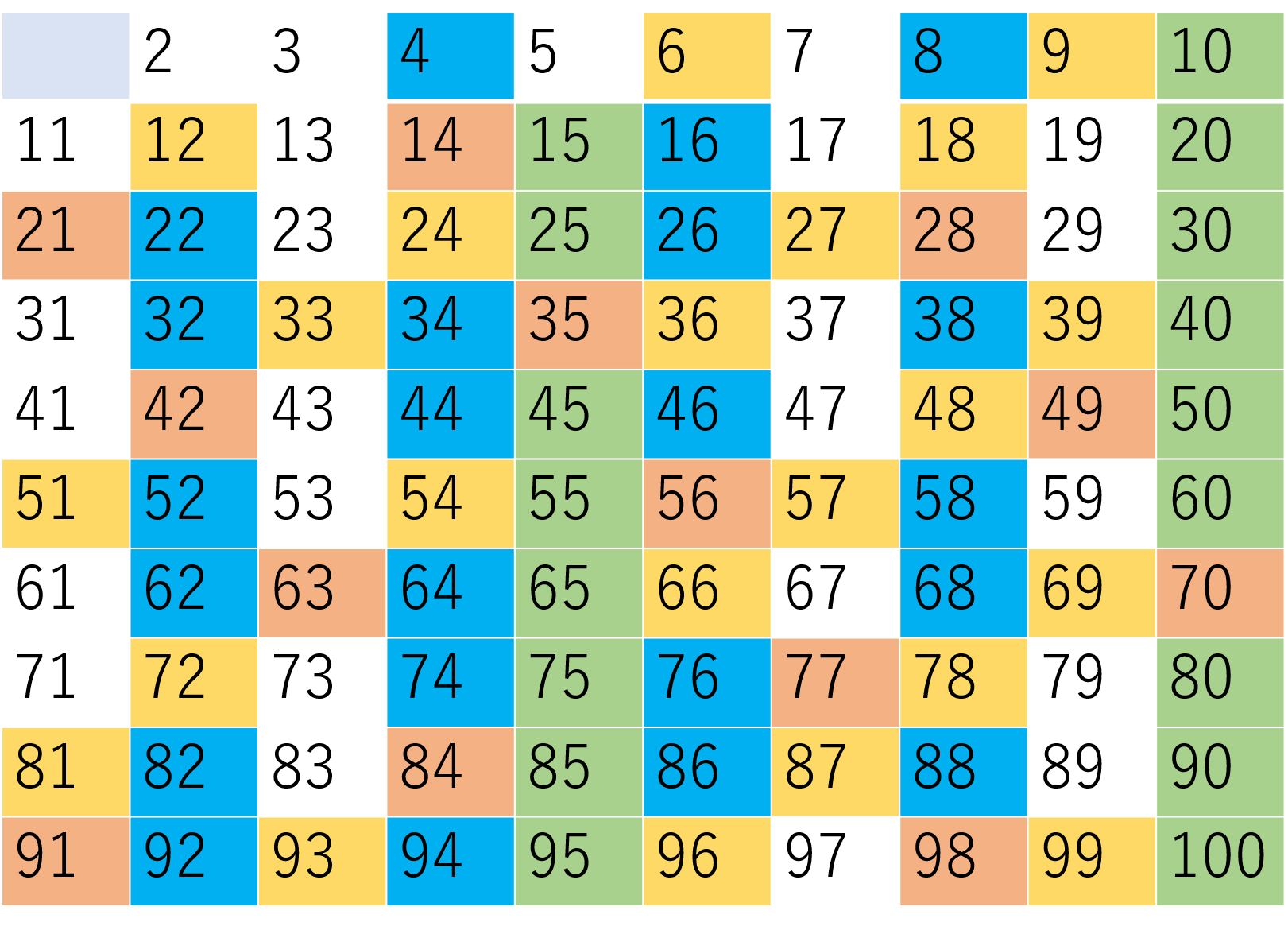
The sieve of Eratosthenes is called the sieve of Eratosthenes because the ancient Greek scientist Eratosthenes devised an algorithm to eliminate multiples of 2 (excluding 2), multiples of 5 (excluding 5), and multiples of 7 (excluding 7) among numbers from 2 to 100 (2 to 120), as shown in the figure below.
The first line calls the math module.
This allows mathematical operations such as sqrt (square root) to be performed.
The third line defines the sieve of Eratosthenes up to number n.
Lines 4, 5, and 6 set up the list of prime numbers up to n + 1, excluding 0 and 1.
Line 8 uses sqrt to put the square root of n into the variable sqrt_n, allowing line 9 to determine the range of i.
In lines 10-12, the variable j (increasing by j) is set to False to indicate that multiples of 2, 3, 5, 7... are to be eliminated.
Line 19 sets the prime number, line 20 specifies the range of p, and line 21 displays p if it exists in prime.
(end=' ' prevents a line break and allows more space between the'and 'characters as they appear.)
Finally, the code is completed by using the sum function to print the number of prime numbers.
The above will realize the sieve of Eratosthenes.