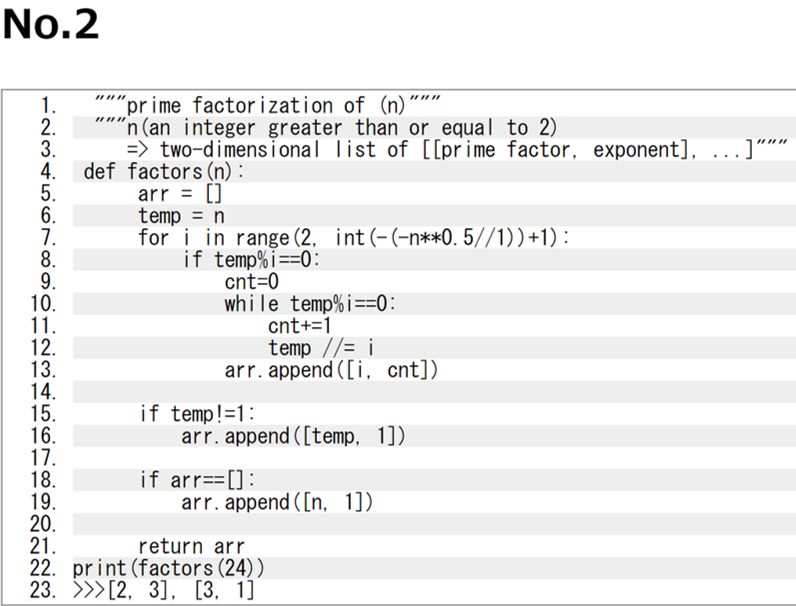
The usual trial division method divides an arbitrary number n by a number between 2 and n-1, but this can be time-consuming as n grows. Therefore, it can be applied as in No. 2.
This code here is a trial division using the property that "the largest prime factor of an integer N is less than or equal to N".
One difference from the usual trial division is that it can be shortened by using exponent to summarize the same prime numbers if they are present, as shown in the second and third lines.
In line 7, the 'int (-(-n**0.5//1)+1' This code uses the above statement, "The largest prime factor of integer N is less than or equal to N," to write the number of prime factors +1. In lines 8 and 9, cnt is used as the exponent.
Line 8 shows that if n (temp) can be divided by i, cnt is initialized first, and lines 10–12 show that if it is divided, the exponent is added by 1.
When it is no longer divisible, exit the loop, add to the list like line 13, and move to line 15.
Line 15 adds the remainder to the list of arr when temp is no longer divisible by i (a prime number).
In lines 18 and 19, the code is to set the list to [1, 1] when the number "1" does not satisfy the above code.
Line 21 completes the program by terminating the factors (n) function and obtaining the list of arr as the return value.
From the above, an applied trial division is realized.