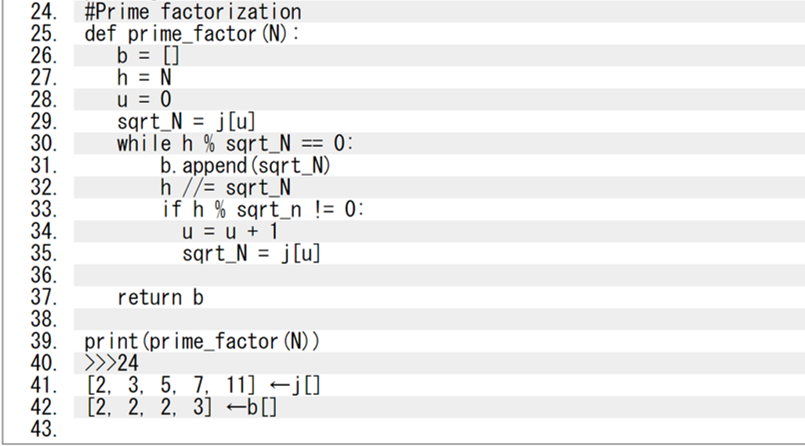
While analyzing and understanding the code of prime factorization and the sieve of Eratosthenes using Google Colaboratory Editor, I thought that to speed up prime factorization, it would be faster to divide by a divisible number in advance than to divide by a prime number and then determine the prime number. This is because a "number" is itself made up of primes or composite numbers that are made by multiplying prime numbers together. Therefore, I thought it would be better to create a table of prime numbers first and then divide by that number.
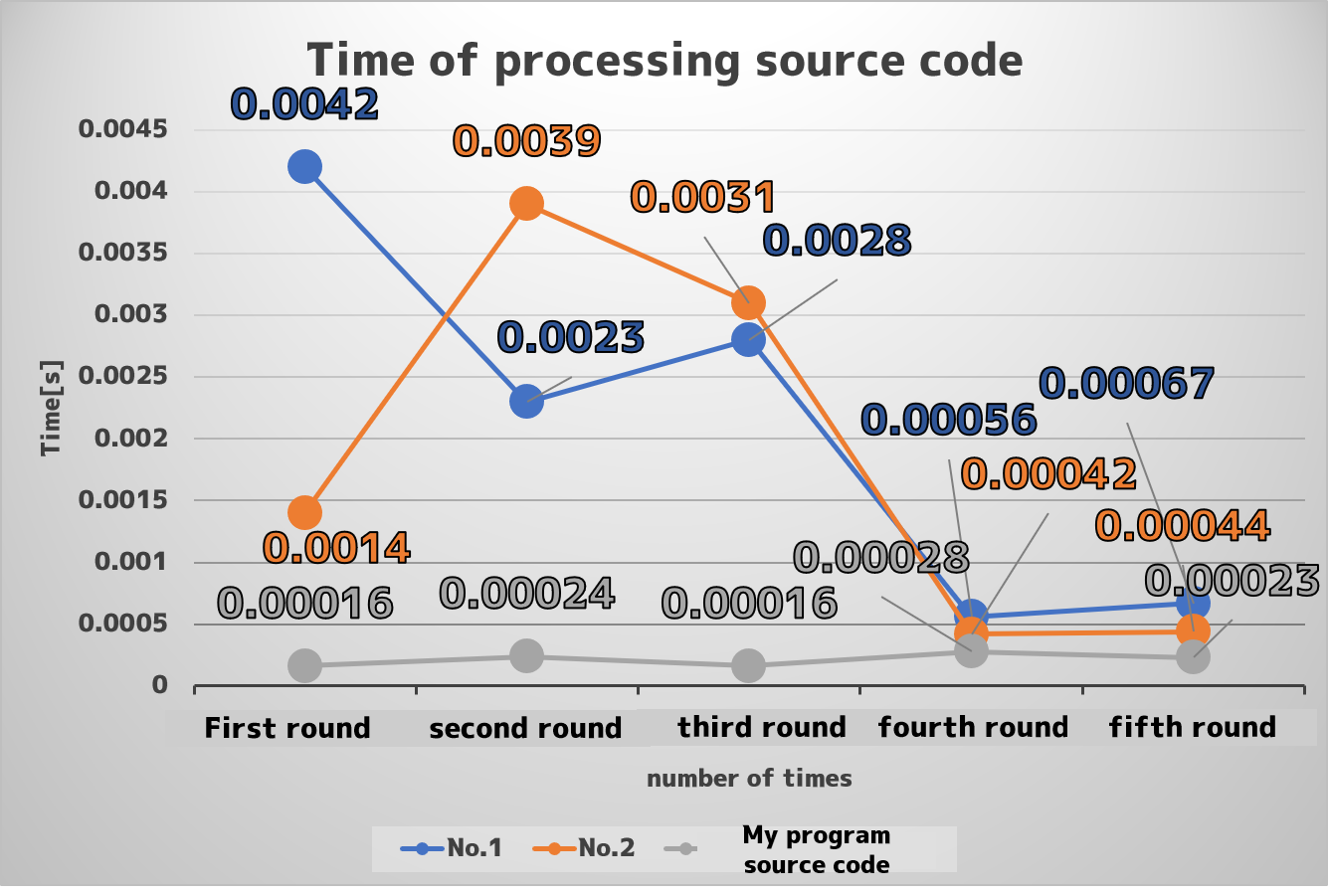
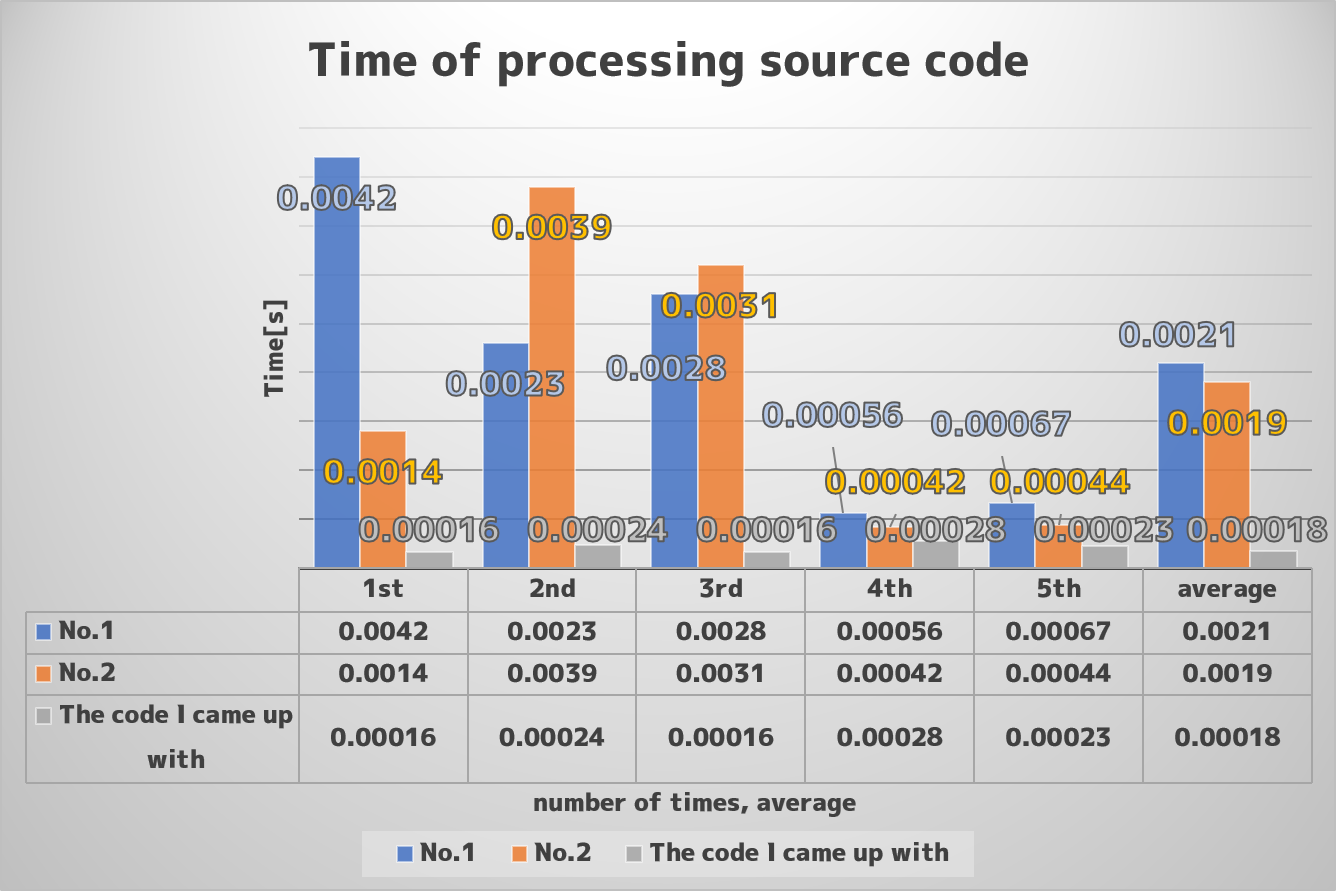
The graph below summarizes the time taken to "prime factorize" the 24 in the code we have done this time, and the reason we did it five times is that there is an error in the time each time it is done, so we needed to take the time in between. The bar graph shows the information from the previous step plus the average.

From this graph, comparing No. 1 and No. 2 in terms of average speed after 5 random runs, we can see that No. 2 is faster. However, we noticed that there are still a lot of random elements, and we cannot completely prove that No. 2 is faster, which is a shortcoming of this study.On the other hand, I discovered that the code I tried this time retains 0.000... time and becomes faster.

Summary and countermeasures

This time we have studied the field of prime numbers and prime factorization through programming.
As I studied the code, analyzed it in my own way, and repeated the process, my knowledge steadily grew, and I came to the conclusion that I wanted to learn more about prime numbers and programming.
In fact, if you know this and that about programming without going into depth, you won't have a hard time with the questions on the common test. But as one of the areas covered in the new subject "Information," it is not just to memorize symbols, not just to say, "This syntax is as this word says."
It is important to grasp the flow of an algorithm.
I thought it was important to grasp the flow as an algorithm and to deepen one's education.
Finally, I would like to talk about the code I came up with myself. I have completed 70% of the code by fully utilizing the code of prime factorization and the sieve of Eratosthenes that I have been studying. The reason why 70% is completed is because I found a flaw: an arbitrary number N can only be divided by a number containing 2, 3, or 5.
I would like to research and fix that defect in the future, and I would also like to use what I have learned this time around for new subjects and so on.

We hope that you will be able to use the knowledge and skills you gain from this field of programming in the future.

Consideration

Summary and countermeasures