11月9日に公開された「情報」のサンプル問題では、第3問でプログラミングについて触れられていました。このことを考慮した上で私は教科書を用いた情報でのプログラミング学習では詳しいところまでは理解できないと考え、素数について調べました。その理由としては素数は現代の暗号化についてネットワークの面で深く関わっているからです。暗号化の代表にはRSA暗号というものがあります。
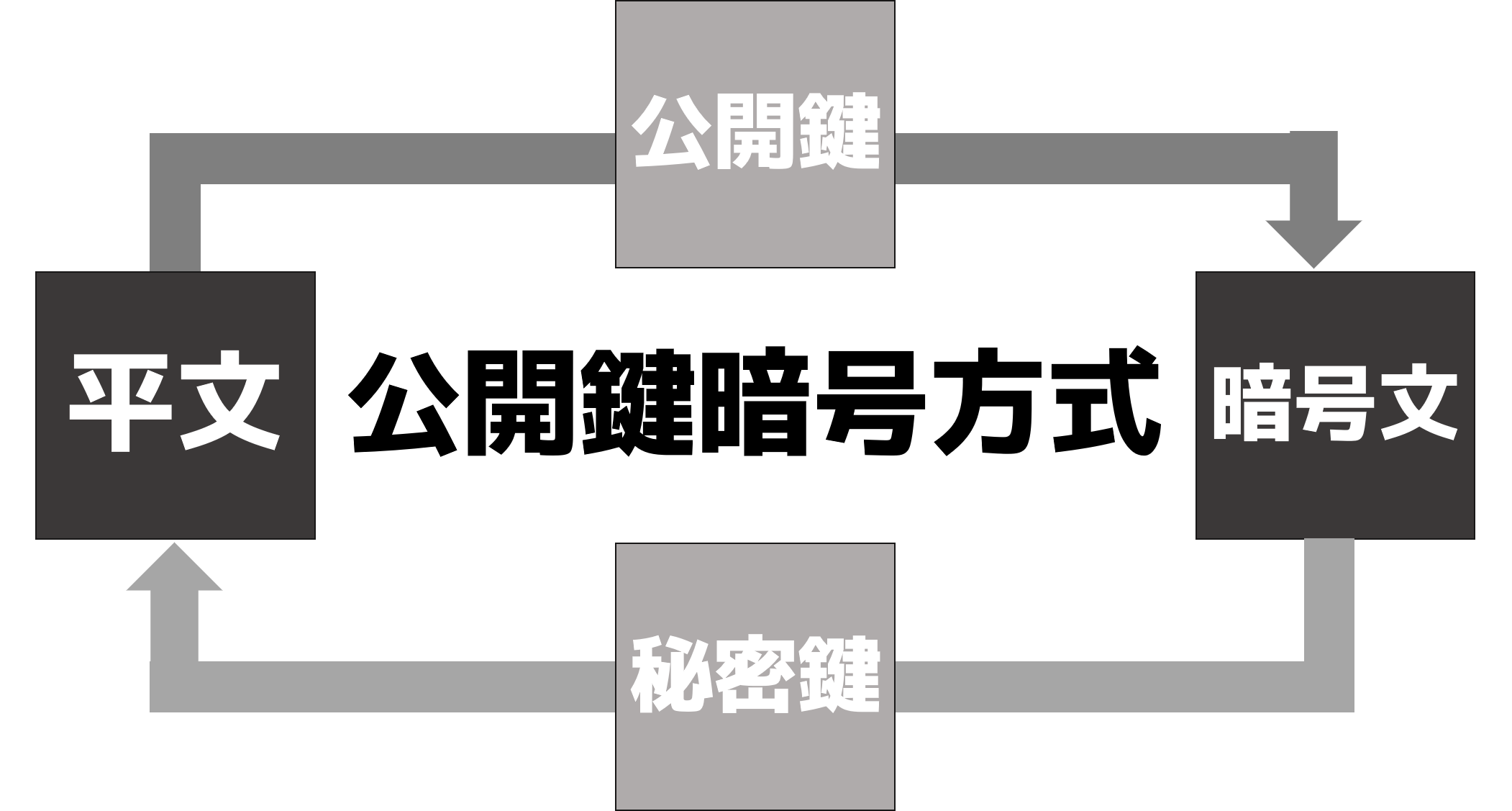
素数というのは任意の数Nについて１とN自身でしか割れない数のことを指します。RSA暗号というのは「素数と素数の積からなる合成数の素因数分解に時間がかかるという性質を安全性の担保としてもつ」ことを用いた最初に実装された '暗号' と 'デジタル署名'　の実現が可能で安全な公開鍵暗号方式の一つです。まずRSA暗号は例えば「2桁の素数と素数の積の15は3×5とすぐ計算できる。しかし、3桁の221とした場合、13×17が出てくるのには多少時間がかかる。さらに4桁と増え3763(53×71)ならば3桁の時よりも時間がかかる。」といったように桁数が増えていくとコンピューターでも解読には時間がかかることを示します。次に公開鍵暗号方式というのは例えば「南京錠を鍵とすると開いた状態の南京錠を公開鍵として、これを開けられる鍵を一つだけ秘密鍵として用意する。受信側が開いた南京錠(公開鍵)を配信し、送信側が自分で鍵を施錠し、受信側に送る。受信側は自分の秘密鍵で解錠することで復号することができる」といったことを言います。(因みにRSAの由来はロナルド・リベリスト、アディ・シャミア、レオナルド・エーデルマンという3人の数学者(発明者)たちの名前の頭文字です。)
ここではプログラミングを通じて素数について理解を深めていきます。

※　次のページから載っているコードは文章の説明に沿い追従します。