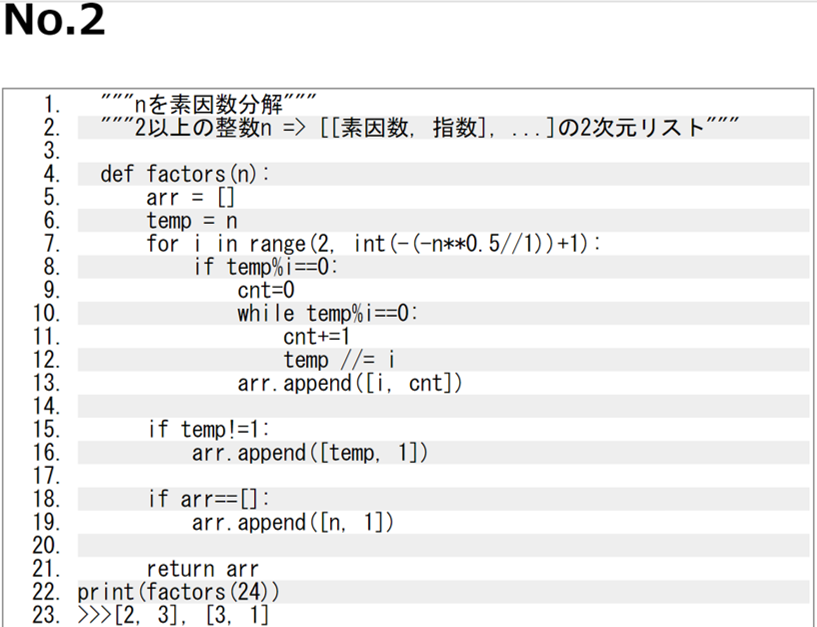
通常の試し割り法では任意の数 n を 2~n-1 の数で割っていますが、これだと n が大きくなると時間がかかることになります。そこで No.2のように応用を利かせることができます。
こちらのコードは「整数Nの最大の素因数は√N以下になる」という性質を利用した試し割り法です。
通常の試し割り法との違いとして2行目の表記の通りに同じ素数があるときに指数を用いてまとめることで時短を図ることができます。
7行目の 'int(-(-n**0.5//1)+1)' このコードは上記の「整数Nの最大素因数が√N以下になる」を用いその素因数+1 の数を記したものです。8,9行目より cnt を指数としています。
8行目ではiで n(temp) を割れるなら cnt をまず初期化し、10行目~12行目では割れたら指数を1ずつ追加していくことを示しています。
割り切れなくなったらループを抜け、13行目の通りにリストに追加し15行目に移ります。
15行目は temp がもう i で割り切れない(素数)時に arr のリストに残りを追加します。
18,19行目では上記のコードを満たさない数 "1" の時にリストを[1, 1]にするというコードです。
21行目で arr のリストを戻り値として得ることで factors(n) の関数を終了させプログラムが完成します。
以上より応用的な試し割り法が実現されます。