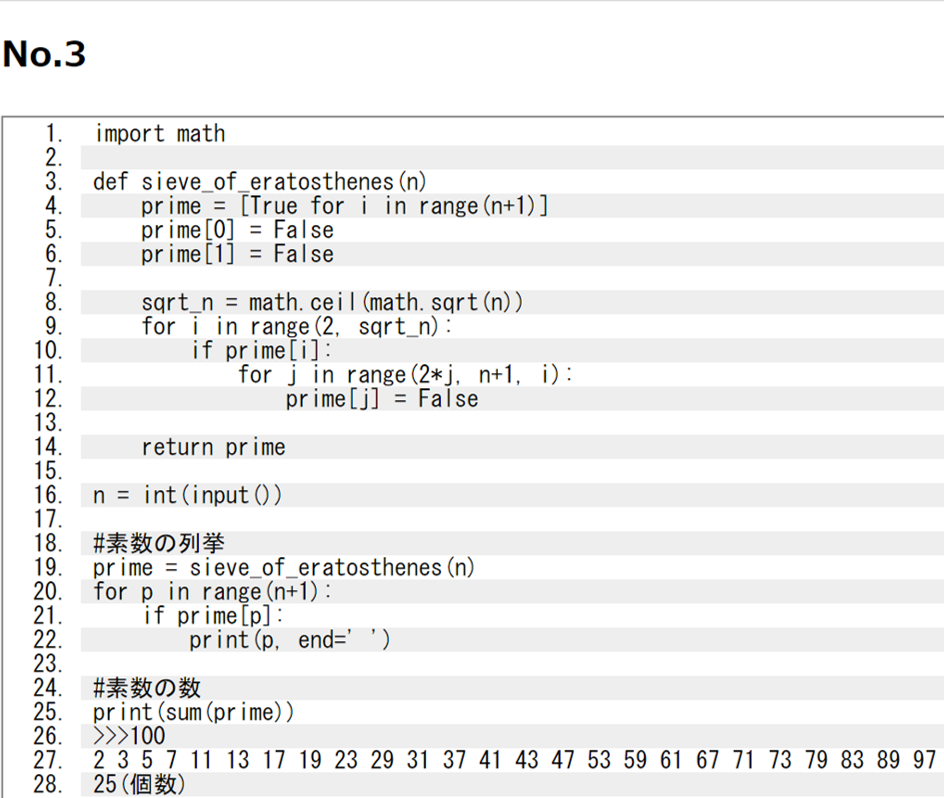
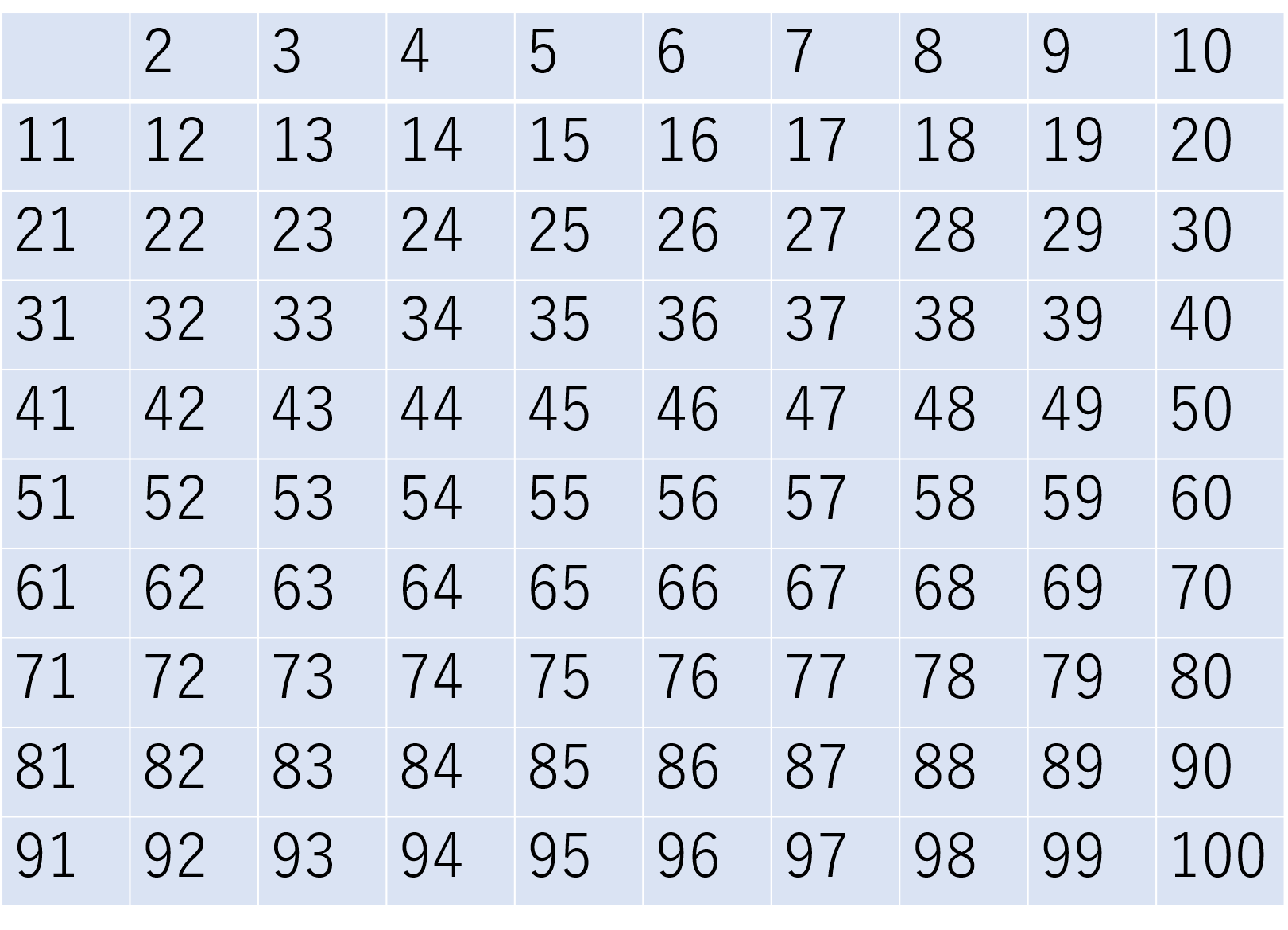
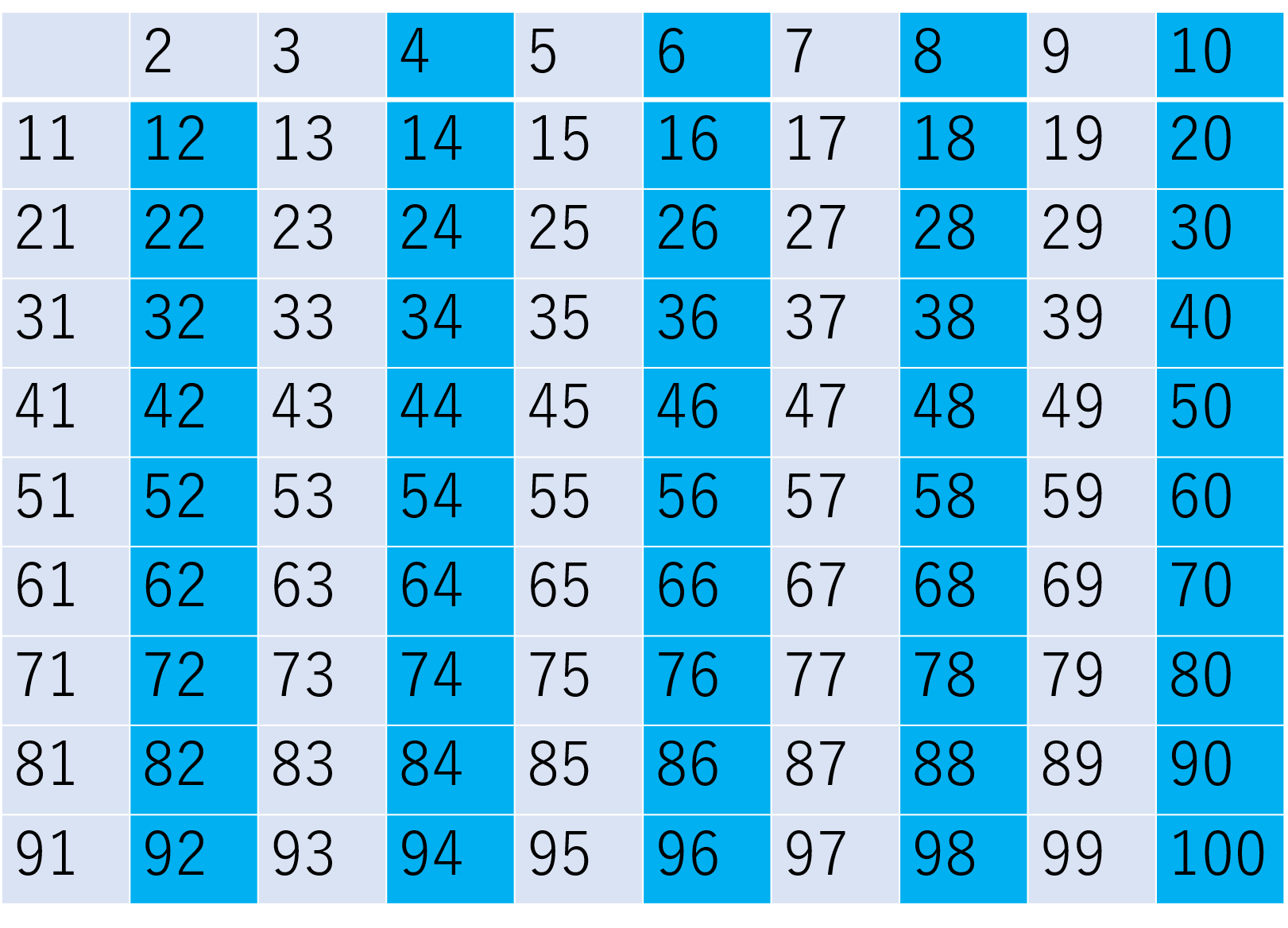
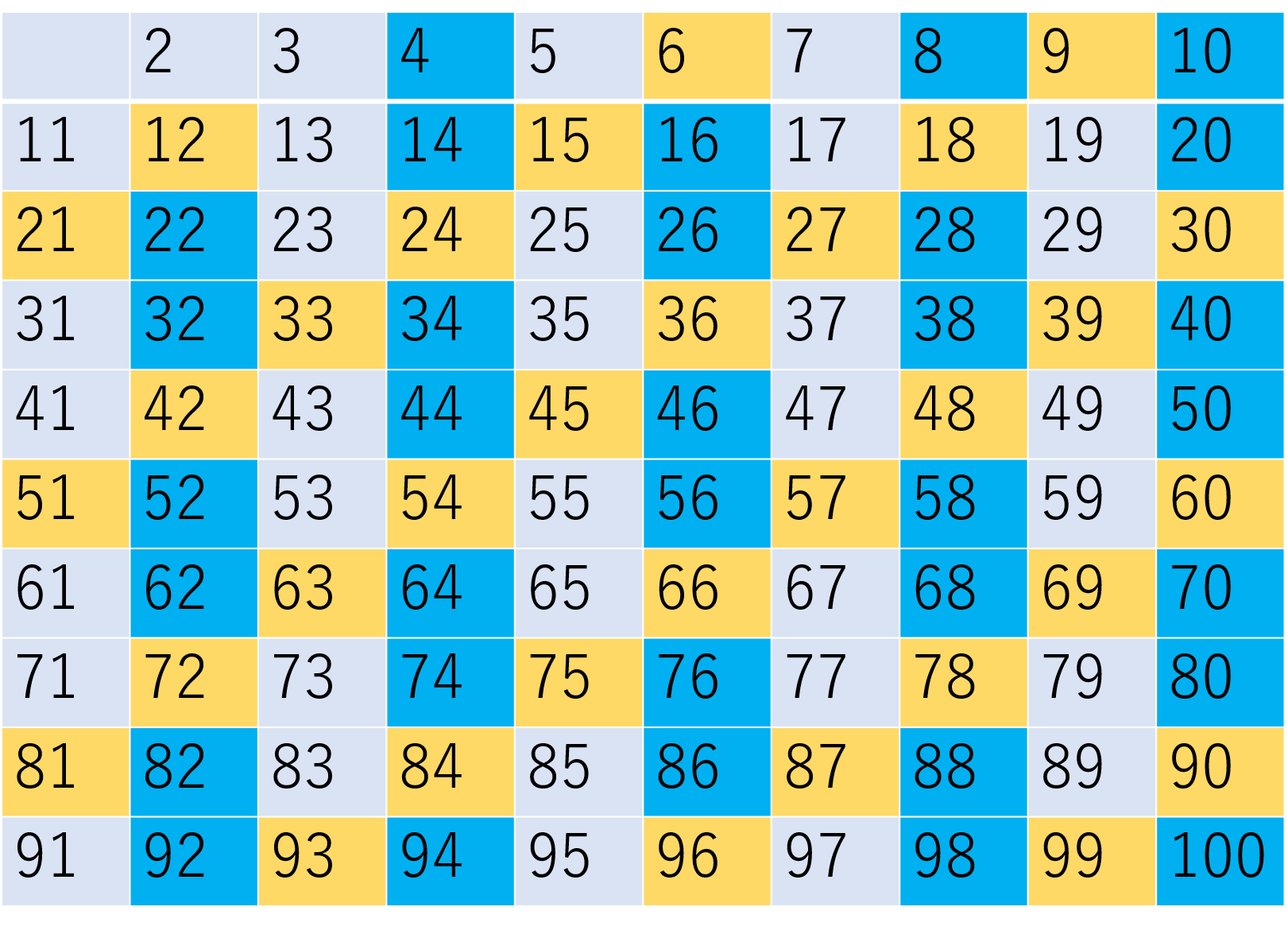
No.1とNo.2の試し割法では素因数分解を用いて素数を出してきましたが、単にどんな数が素数かを探すためにエラトステネスの篩というものが使われます。
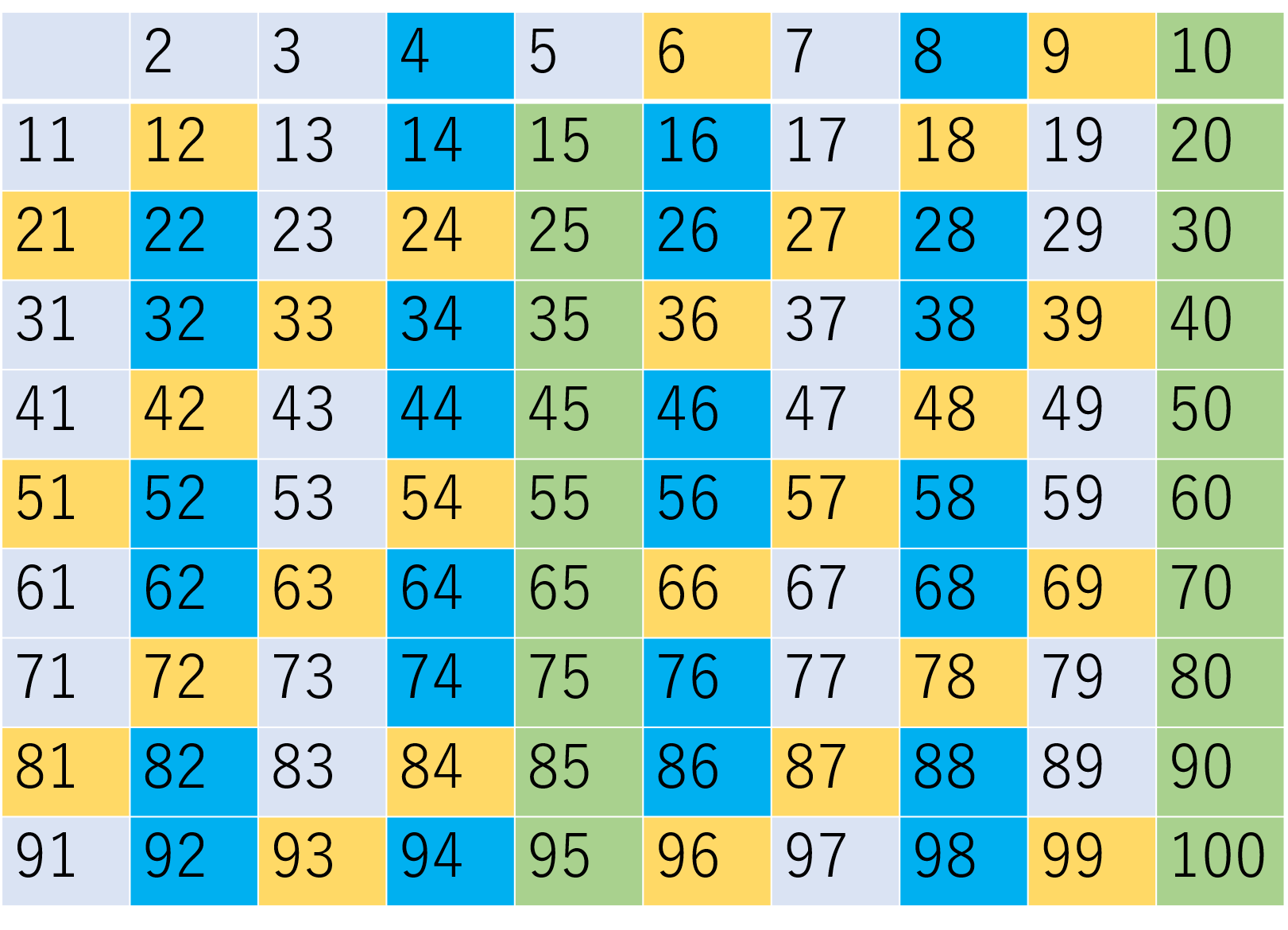
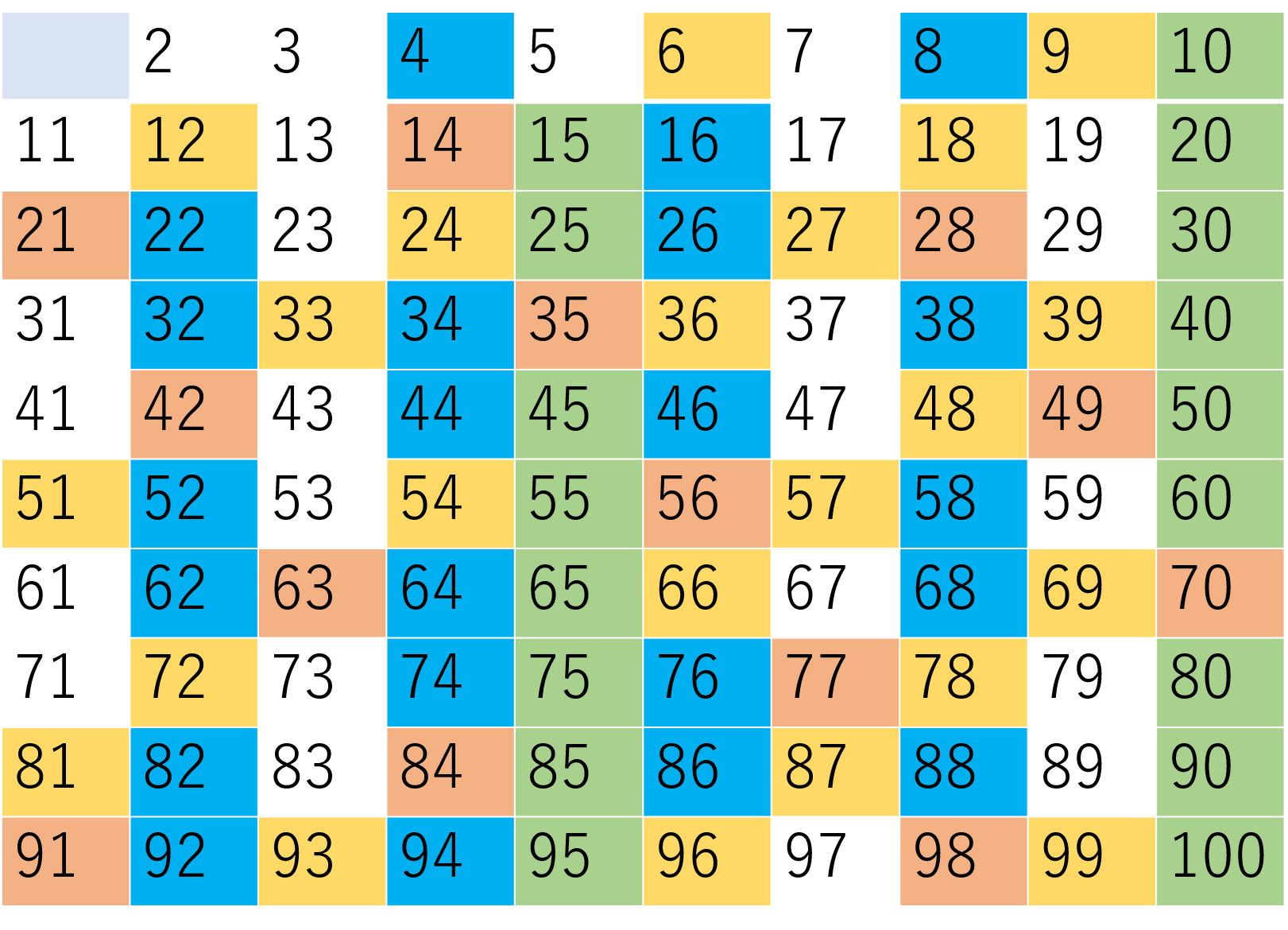
エラトステネスの篩というのは下図のように2~100(2~120)の数の中で2の倍数(2を除く)、5の倍数(5を除く)、7の倍数(7を除く)といったものを篩にかけるように消していくアルゴリズムを古代ギリシャの科学者であるエラトステネスが考案したことからエラトステネスの篩と呼ばれています。
まず1行目で math モジュールを呼び出しています。
そうすることで sqrt(平方根) といった数学的処理を行うことができます。
3行目では数nまでにエラトステネスの篩を使うことを定義しています。
4,5,6行目で0,1を除く n + 1 までの素数のリストを設定します。
8行目では sqrt を使いnの平方根を変数 sqrt_n に入れることにより9行目で i の範囲を決めることができます。
10~12行目で変数 j (jずつ増やす) を False にすることで2,3,5,7・・・の倍数を消すことを表しています。
19行目で素数 prime を設定し20行目で p の範囲を指定し21行目で prime にpがあるならばそれを表示させることになります。
(end=' ' は改行をさせないようにするかつ ' と ' の間をあけることで出てくる文字の間隔をあけることができます。)
最後にsum関数を使い素数の数を表示させることでこのコードは完成します。
以上によりエラトステネスの篩が実現されます。