
相関分析・回帰分析
データにはいろいろな種類があるけど、レイさんはどんなデータを分析するんだい?

自分は高齢者数と空き家の関係を調べようと思って...
じゃあ相関分析をして相関を調べるのかな?

ん?いやただ表を出すだけですけど...
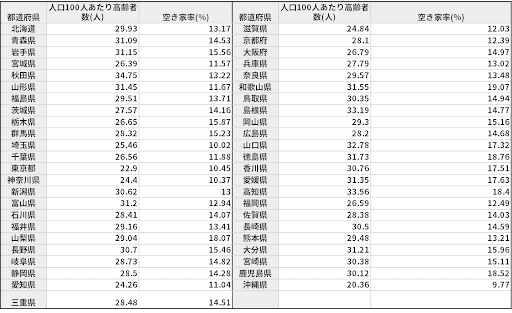
いやいや、それはただ単にデータを並べただけだよ。先生が話してたように相関分析までやってみたら?
え、じゃあ相関分析について知らないと...
では相関分析を一緒に実践しながら説明しよう。

この章で知っておくべき言葉
母集団...調査を行いたい対象全体のこと
母平均...母集団の平均
母分散...母集団の分散
抽出...母集団から無作為に選び出すこと
標本...抽出された集団のこと
標本平均...標本の平均
標本分散...標本の分散
サンプル数...一組の標本中のデータ数
相関分析・回帰分析
※今回はGoogleスプレッドシートを使用して説明します。
元々相関というのは分析する対象が変化したとき、もう一方も同様に変化するというような互いに関係を持つ関係である。相関分析や回帰分析は2つの要素が関係しているのかを分析するために用いられる分析方法である。

散布図
相関分析とは2つの要素の関係を分析することであり、データの関係を表現するグラフとして散布図で表される事が多い。googleスプレッドシートでは二つの範囲を選択し、「挿入」→「グラフ」でグラフが表示される。グラフが散布図でない場合、「グラフの種類」から「散布図」を選択する。
※動画で実践している。
では先ほどのデータを実際に散布図にしてみよう。

こうかな?
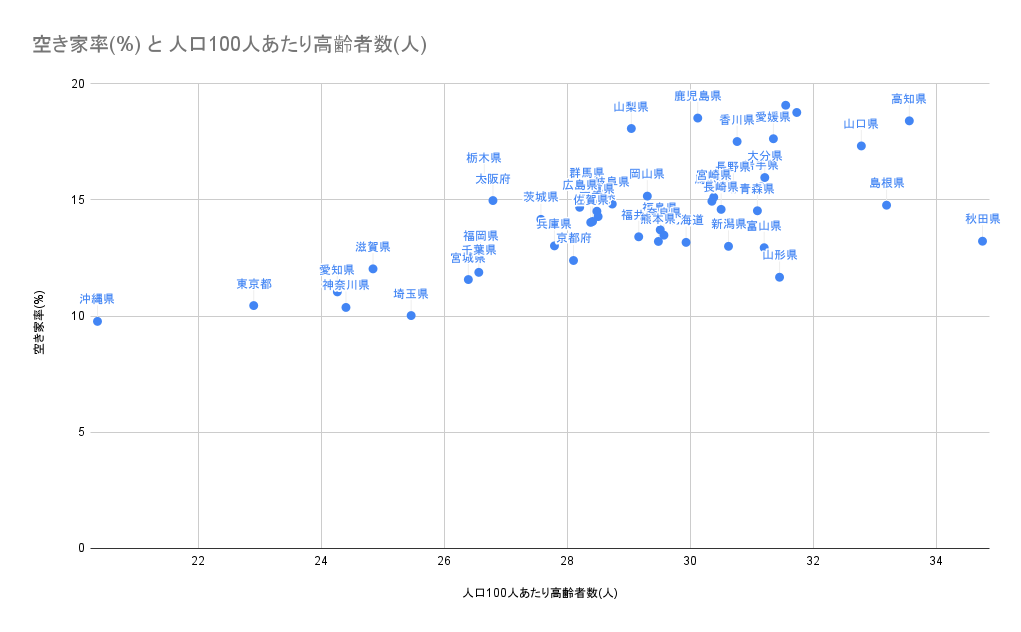
そうだね。次に相関を可視化するために回帰直線を作ろう。

回帰直線?
確か一次関数みたいなグラフを作るんですよね。
そうだね、実際にやってみよう。

回帰直線
散布図で表された値を一次関数と仮定して近似させ、y=ax+bのようにした線のこと。この直線は各データの直線との差(残差または誤差)を二乗した値の合計をとった最も値が小さくなる直線の関数となっており、この方法は最小二乗法と呼ばれている。今回の回帰直線の式はy =0.547*x + -1.58となっている。
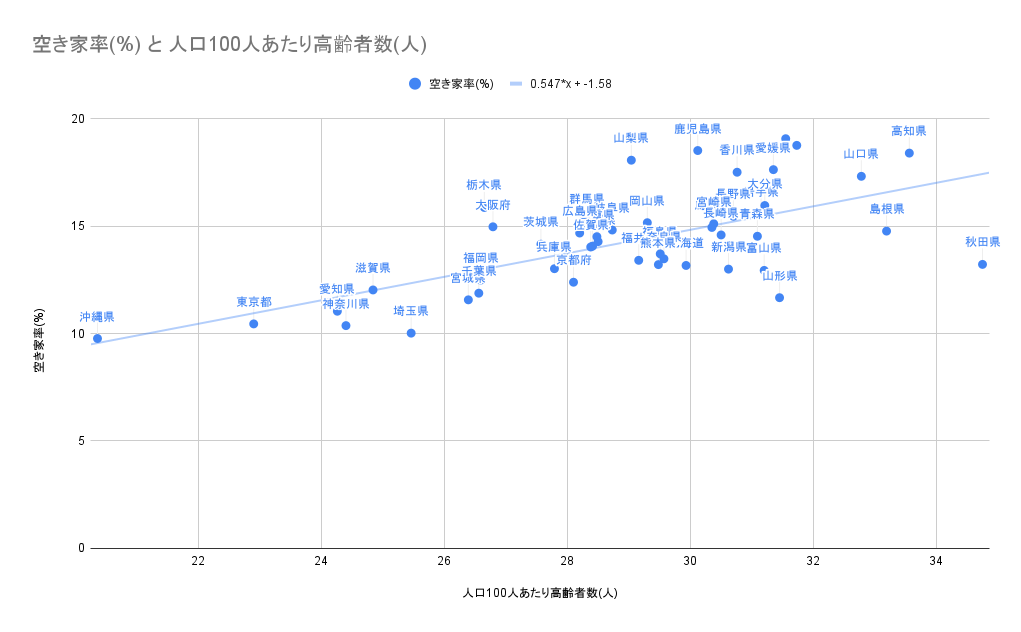
相関係数は標準偏差と同じように関数を使って計算できるんですか?
もちろん、CORREL関数を使えばできるよ。でも、一応計算方法も見てみよう。

相関係数
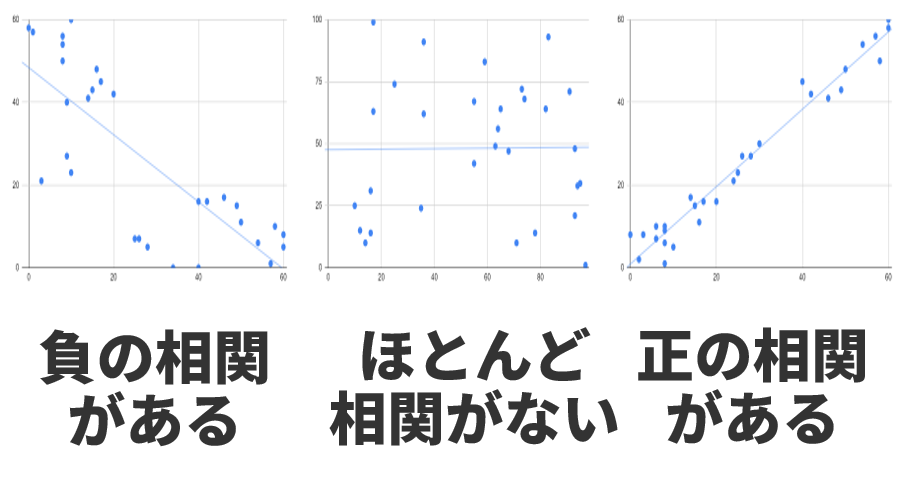
相関係数は二つの要素の関係の強さを数値化した値であり、-1から1の間で表される。それぞれ絶対値が1に近いほど相関が強い。

相関係数はそれぞれのデータをXとYとすると、図のように共分散(偏差X × 偏差Yの平均)をXとYの標準偏差を掛けた値で割った値である。このように、相関係数を求めるにはそれぞれ平均と偏差、標準偏差、共分散まで求める必要がある。
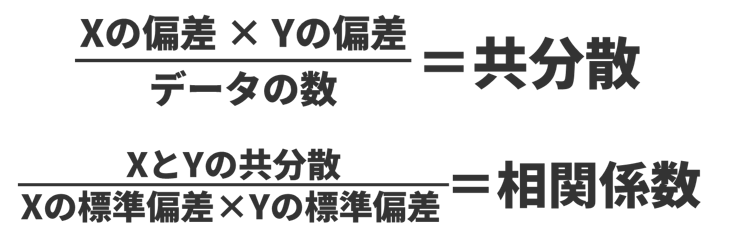
CORREL関数(相関係数)
相関係数を求めるときにはCORREL関数使い、=CORREL(範囲X,範囲Y)を使う。CORRELは英語で、correlation coefficient(コリレーション・コエフィシェント)という言葉が由来になっている。今回は図のように空白のセルに「=CORREL(B4:B50,C4:C50)」とすると、B3からC50までの数値の相関係数を求めることができる。
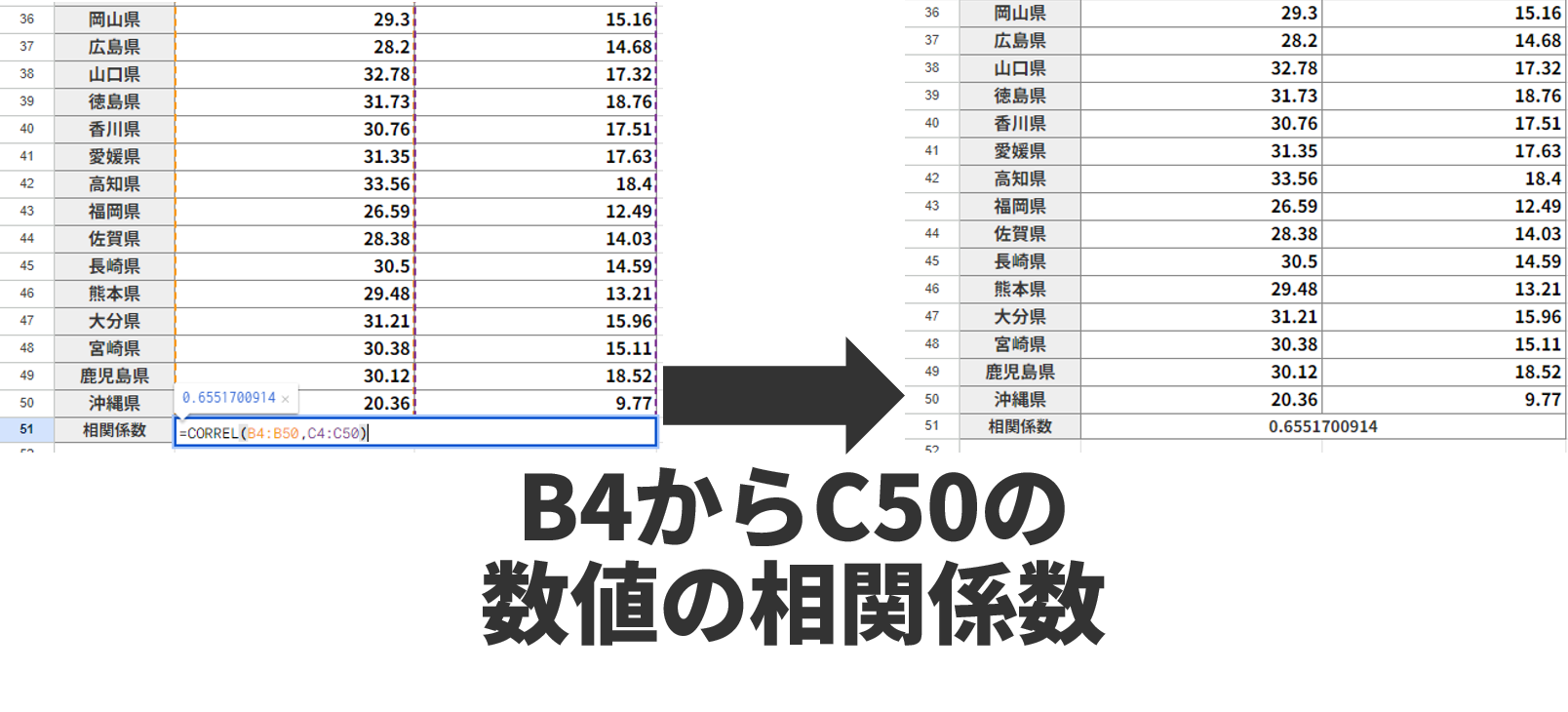
本当に簡単にできた!相関係数が約0.66ということは...正の相関があるね!
ということは高齢者が多いほど空き家の割合が高い傾向があるんですね。
相関分析と回帰分析ってやってみると楽しい!
それは良いことだ。自分で実践することは大事だからね。でも、この後説明することには気を付けてね。

疑似相関
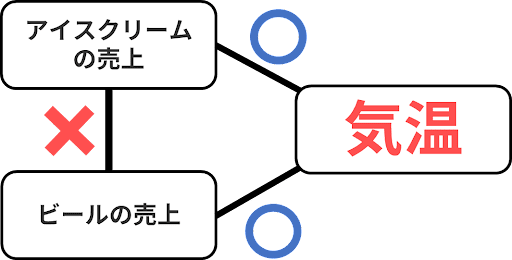
疑似相関は別名見せかけの相関ともいい、二つの事象の間に相関が見られるが、因果関係は存在しない状態を表す。例えば、アイスクリームの売り上げとビールの売り上げは強い正の相関がある。しかし、これには第3の変数である気温が共通の変数となっている。そのため、気温とアイスクリームの売り上げと気温とビールの売り上げの分析はできるが、アイスクリームの売り上げとビールの売り上げを分析してはいけない。このように、回帰分析や相関分析をするときは因果関係と相関関係がどちらも必要となる。
そっか、何でも因果関係があるとは限らないんだね。今度から気をつけよう。
回帰分析や相関分析をするときは因果関係も成立しているか確認して分析しよう。

- ①データの相関関係を調べるとき、回帰分析や相関分析をする。
- ②分析する際、擬似相関に気を付ける。

